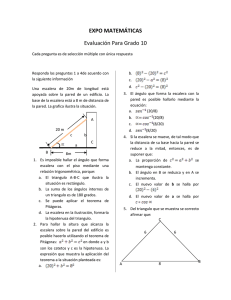
Linea de Visión Horizontal Linea de Visión Horizontal
Anuncio

2.1.2 Aplicaciones que originan triángulos rectángulos. Los problemas cuya solución está relacionada con un triangulo rectángulo, se puede resolver teniendo en cuenta el Teorema de Pitágoras y las definiciones de funciones trigonométricas en el triangulo rectángulo. 2.1.2.1 Ángulo de Elevación y ángulo de Depresión Los triángulos rectángulos se utilizan frecuentemente para hallar distancias que no pueden medirse fácilmente en forma directa. En tales casos se utiliza el ojo, del investigador como punto de referencia. Se llama Línea de visión a la recta imaginaria que une el ojo de un observador con el lugar observado; Angulo de Elevación (figura .6 al que forman la horizontal del observador y el lugar observado cuando éste está situado arriba del observador. Cuando el observador está más alto se llama ángulo de Depresión (figura .7 Figura .6 Angulo de elevación ión is eV ad e Lin Horizontal Figura .7 Àngulo de Depresión Horizontal Lin e ad eV isió n Ejemplo 5: El ángulo de elevación con que se mira la veleta de una torre es de 45.25º, cuando el observador se coloca a 72m de la torre. Si el observador se encuentra a 1.10 m sobre el suelo, ¿a qué altura se encuentra la veleta? Solución Si se observa la figura .8- Veleta de una torre y de acuerdo al problema, se ve que se forma un ángulo de elevación y el problema se reduce a encontrar el lado h del triangulo rectángulo de la figura 9, triangulo de la veleta de una torre. figura 8- Veleta de una torre 45,25o 1,10 m 72 m h figura 9, triangulo de la veleta de una torre. 45,25o 72m Para hallar la altura, la función trigonométrica es la función tangente. Como el observador, está a una altura de 1.10 del piso, altura veletta=1.10+72.63 altura veletta=73.73m Ejemplo 6: Se desea calcular la altura de una torre de lanzamiento de cohetes. Para ello se hacen dos observaciones desde los puntos A y B, (Figura 10) obteniendo como ángulos de elevación 30º y 45º respectivamente. La distancia entre AB es de 30m. Hallar la altura de la torre. Solución Figura 10-lanzamiento de cohete. C h 30o A x=30 45o B y P Con los datos del problema y los datos de la gráfica anterior, se puede concluir: • Se forman dos triángulos rectángulos APC y BPD • La altura es común para ambos triangulo (h) • La base o cateto adyacente del triangulo APC es 30+y • La base o cateto adyacente del triangulo BPD es y • El ángulo A es de 30º y del ángulo B es de45º. • Se puede trabajar con las tangentes para ambos ángulos, formar dos ecuaciones y dado que la altura es común para ambos triángulos se halla el valor de h por solución de ecuaciones simultáneas. El problema queda: • Despejando h de la ecuación 1 y de la ecuación 2 • Igualando las dos ecuaciones resultantes • Solucionando la ecuación anterior • Llevando a un solo lado los términos de “y” • Sacando factor común • Despejando a “y” • Reemplazando el valor de y en la ecuación 2 y despejando h, La altura de la torre es d e 40.9 8 m Ejemplo 7 Un vigilante se encuentra en la ventana del faro a una altura de 35m (ver figura 11), sobre el nivel del mar. El ángulo de depresión del barco es de 30º. Cual es la distancia del barco al faro? C Solución 30o o 60 35m Figura 11-ejercicio del Faro d Llevando la figura anterior a un triangulo rectángulo (ver figura 12 se tiene: 60o figura 12 triángulo del ejemplo 7 35m d De acuerdo a la figura anterior y la información que se tiene del problema, • Por ángulos complementarios, el ángulo interno es igual a 60º • La altura del faro = 35m • Se halla la distancia “d”. • Trabajando con la función tangente de 60º, • Despejando a “d”. La dista ncia d el barc o al faro es d e 60 .62m


![Evaluación%20Grado%20Decimo%20noveno%20y%20undecimo[1].](http://s2.studylib.es/store/data/000860011_1-723727629aa8ab5007657ff23e4e4a09-300x300.png)