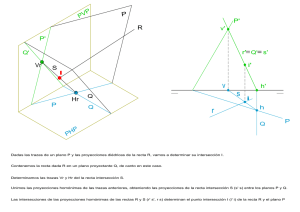
Intersecciones y Ordenamiento

INTERSECCIONES
El cálculo de intersecciones en el espacio tiene varias finalidades en CG. La más simple es el clipping:
el recorte de los objetos entre los límites del volumen visual, renderizando sólo la fracción visible de la
escena. Las aplicaciones más complejas y masivas se dan al hacer ray-tracing y sus derivados, para
utilizar modelos de iluminación y sombreado más realistas, allí hay que calcular una miríada de
intersecciones entre rayos y objetos de la escena. También se utilizan para detección de colisiones en
simulaciones y juegos o detección de interferencias entre objetos de CAD. Las aplicaciones en
geometría computacional abarcan también los procesos de generación de mallas y la determinación de
isocurvas e isosuperficies para visualización de datos.
Veremos algunos ejemplos para mostrar los métodos básicos y alternativas. En la mayoría de los
libros, los planos y las rectas están definidas en forma vectorial o implícita, aquí utilizaremos también
el tratamiento paramétrico, que ya aprendimos a manejar para las curvas y superficies.
Se pretende que los algoritmos empleados sean rápidos, precisos y robustos. La falta de robustez
hace que los errores salten inmediatamente a la vista. Siempre es preferible sacrificar la precisión en
aras de la robustez: que el código entregue un resultado útil en cualquier caso, aún con un pequeño
margen de error. El usuario no se da cuenta si el punto de intersección debería estar un píxel más aquí
o allá, pero enseguida nota un píxel mal pintado o el ruido de colores del z-fighting; dando resultados
visualmente inaceptables; o peor, un “cuelgue” del programa.
El requerimiento de velocidad se vuelve obvio si se piensa que un procedimiento de ray-tracing, por
ejemplo, debe analizar intersecciones entre millones de rayos y miles de objetos. La primera respuesta
que hay que dar, y muy rápidamente, es si puede o no existir la intersección. Veremos las técnicas de
partición del espacio que nos permiten acelerar estas consultas y realizar descartes masivos muy
rápidamente. La velocidad de las placas gráficas se mide mediante la capacidad de procesar polígonos
rápidamente, el polygon throughput está en el orden de los 100 millones de polígonos por segundo.
Pertenencia y Distancia de Punto a Recta y Plano
La distancia entre dos objetos es la menor de entre las distancias de sus puntos. De un punto a un plano
o a una recta es la distancia al pie de la perpendicular del punto al plano o recta.
P
P
d
d
P┴
P1
P2
P┴
P0
P0
P1
P
P
d
P┴
P1
P0
d
P2
P┴
P0
P1
1/12
En el caso de la recta, definida por P0 y P1, notemos que el paralelogramo que subtienden los vectores
P1–P0 y P–P0 tiene altura d, que es la distancia buscada. El área del paralelogramo se calcula mediante
el producto vectorial. La distancia del punto a la recta (altura) se puede calcular mediante el área del
paralelogramo (base x altura) dividida por la longitud de la base, que es el módulo del vector P1–P0.
(P−P0)×(P1−P0)
(P1−P0)
d(P,{P0,P1}) =
= (P−P0) ×
||P1−P0||
||P1−P0||
En el caso del plano {P0, P1, P2} sucede lo mismo, pero con el paralelepípedo formado por los tres
vectores basados en P0 y cuyo volumen se calcula mediante el producto mixto. La distancia del punto
al plano (altura) será el volumen del paralelepípedo (área de la base x altura) dividido por el área de la
base que es el módulo del producto vectorial:
(P−P0)·(P1−P0)×(P2−P0)
(P1−P0)×(P2−P0)
d(P,{P0,P1,P2}) =
= (P−P0) ·
||(P1−P0)×(P2−P0)||
||(P1−P0)×(P2−P0)||
En ambos casos, si el resultado es nulo, el punto pertenece a la recta o al plano.
Una “distancia” es un real sin signo; por lo tanto las ecuaciones de arriba tienen datos demás. El
resultado de la primera ecuación es un vector; es normal al plano definido por la recta y el punto y su
módulo es la distancia buscada; la dirección del vector nos indica un punto de vista desde el cual el
punto está a la derecha de la recta en ese plano. Para la otra ecuación, la distancia calculada al plano es
un escalar con signo y el signo indica de qué lado del plano está el punto.
Los vectores que quedan a la derecha, divididos por sus módulos, son el versor tangente o dirección de
la recta y el versor normal al plano respectivamente.
(P1−P0)
(P1−P0)×(P2−P0)
t=
n=
||P1−P0||
||(P1−P0)×(P2−P0)||
El pie de la perpendicular o proyección se puede calcular del siguiente modo:
(P┴−P0) = [(P−P0)·t] t
(P┴−P0) = (P−P0) − [(P−P0)·n] n
Siendo t y n versores (módulo uno), la primera ecuación es simplemente la proyección de P sobre la
recta. En la segunda ecuación, al vector P−P0 se le quita la componente normal al plano: [(P−P0)·n] n
−que es la proyección sobre una recta perpendicular− quedando sólo la componente en el plano.
El cuadrado de la distancia se puede calcular también por medio de las proyecciones normales:
d2 = (P−P0)2 − [(P−P0)·t]2
d2 = [(P−P0)·n]2
En caso de que se desee calcular sólo la pertenencia o no al plano o recta, o de que lado está el punto,
no hacen falta los módulos ni las divisiones, los cuadrados y los numeradores se comparan con cero.
En general, hay que evitar raíces y divisiones para ganar en velocidad y robustez. Por ejemplo:
comparar distancias es lo mismo que comparar cuadrados y no implica extraer raíces.
Intersecciones de Líneas y Planos o Segmentos y Triángulos
Para calcular la intersección de dos segmentos hay que plantear la intersección de las rectas que los
soportan. Si cada recta se define como expansión afín de los dos puntos del segmento, su intersección
se calcula mediante la igualación del punto variable:
(1−α)P0+αP1 = (1−β)Q0+βQ1
Para dos rectas en el plano, son dos ecuaciones (x, y) con dos incógnitas (α, β). Si la matriz es singular
las entidades son paralelas o coincidentes. Si la intersección existe, los valores de los dos parámetros
nos indican si la intersección se produce dentro o fuera de cada segmento.
En el espacio son tres ecuaciones con dos incógnitas, cada par de ecuaciones nos da los parámetros en
la intersección vista desde el correspondiente plano coordenado, si la intersección existe coinciden las
tres proyecciones. Se pueden calcular α y β con las ecuaciones para x e y; luego, si existen y están
entre cero y uno, se verifica la ecuación para z. Este método es muy poco robusto pues depende de si
alguna de las rectas se ve de punta (se ve como un punto) en el plano xy (o en otros).
Un método más robusto y elegante (independiente del triedro de referencia) se basa en usar la
proyección sobre una normal a ambas rectas. En esa proyección, si existe, se mide la distancia entre las
rectas de soporte y, si es nula, luego se interpola el punto de intersección.
2/12
Los detalles son así:
n = (P1 – P0) × (Q1 – Q0) = ∆P × ∆Q
n
Q1
Si n = {0,0,0} las rectas son paralelas o coincidentes. En caso
contrario, se verifica si están alabeadas en el espacio:
Q0
2
2
d = ((Q0 – P0) · n) n/n = (∆0 · n) n/n
d
P
0
Ese vector tiene por módulo la distancia entre las rectas y es
perpendicular a las dos. Si es nulo, las rectas se cortan en el
espacio y hay que interpolar la intersección. Notar que no hizo
falta calcular una raíz cuadrada para el módulo de n, basta con
utilizar n2 = n·n y además, para saber si forman un plano, basta
verificar si ∆0· n se anula, sin dividir.
P0
Para interpolar I, usamos las áreas de los triángulos que se forman
∆P
I
con ∆Q fijo y los puntos de P (o viceversa). El área entre ∆Q y
∆0
P0, por ejemplo, es (P0−Q0)×∆Q/2 pero como necesitamos el
Q0
signo y vemos que da un vector en la dirección normal,
calculamos un valor proporcional (multiplicado por 2||n||) y con
signo: A(P0) = (P0−Q0)×∆Q⋅n. El cero interpolado es el área que corresponde al punto I:
A(I) − A(P0)
0 − (P0−Q0)×∆Q⋅n
(Q0−P0)×∆Q⋅n ∆0×∆Q⋅n
α = A(P ) − A(P ) =
=
=
.
(P1−Q0)×∆Q⋅n−(P0−Q0)×∆Q⋅n (P1−P0)×∆Q⋅n ∆P×∆Q⋅n
1
0
P1
Q1
∆Q
P1
∆0×∆Q⋅n
∆0×∆P⋅n
y, del mismo modo: β =
n2
n2
Solo resta verificar que α y β estén entre 0 y uno y calcular I = P0 + α ∆P.
Resumen de implementación:
a) ∆P, ∆Q, n = ∆P×∆Q. Si n≠{0,0,0} ⇒ b)
b) Si ∆0·n = 0 ⇒ c)
c) b = n×∆0, α’ = b·∆Q, β’ = b·∆P. Si {α’,β’} ∈ [0,n2]2 ⇒ d)
d) I = P0 + α’/n2 ∆P
α=
La intersección de un segmento (o rayo) y un triángulo en el
espacio es la situación más usual y, por suerte, es mucho más
sencilla; es un sistema de tres ecuaciones y tres incógnitas.
(1−α)P0+αP1 = (1−β−γ)Q0+βQ1+γQ2
Una matriz singular de coeficientes indica que las entidades son
paralelas o coincidentes y además los parámetros entre cero y
uno indican la pertenencia de la intersección al segmento y al
triángulo. Si se trata de una recta, α no importa; si se trata de un
rayo o semirrecta, α indica si la intersección está delante o
detrás del punto de partida P0 y además puede servir para
calcular la distancia al ojo (z-buffer).
Q2
P1
Q0
P0
Q1
La intersección de dos triángulos es un segmento en la recta de intersección de sus planos. En este caso
los parámetros son cuatro (dos de cada triangulo)
P0
y tenemos tres ecuaciones, por lo que el resultado
tiene un parámetro variable que define justamente
Q0
I
la recta de intersección. De todos modos, haremos
un análisis más sencillo, pero diferente.
np
Calculamos primero las normales como productos
nq
vectoriales de dos aristas en cada triángulo. Los
planos son paralelos o coincidentes si las normales
son paralelas. En caso contrario, la recta de
t
3/12
intersección pertenece a ambos planos y por lo tanto es perpendicular a ambas normales. La dirección
de la recta es: t = np×nq, pero para terminar de definir la posición de la recta en el espacio hace falta un
punto. En el plano definido por las dos normales, los triángulos se ven como segmentos y la recta se ve
como un punto I, que se puede calcular como la intersección de los segmentos, pero es más sencillo
considerar que I−P0 es perpendicular a np y que I−Q0 es perpendicular a nq, para calcular las
componentes en el plano:
I = δ np + ε nq
(I−P0 )·np = 0
⇒
δ np·np + ε np·nq = P0·np
⇒
δ np·nq + ε nq·nq = Q0·nq
(I−Q0)·nq = 0
Es un sistema de 2x2 del que se obtienen δ y ε y por lo tanto I y queda definida la recta.
Finalmente se intercepta la recta (I + α t) con las aristas ((1-β) Pi +β Pj) para definir la intersección de
los triángulos. Por cada β ∈ [0,1) obtenemos un valor de α y un punto. Si obtenemos dos puntos por
triángulo, ordenando los valores de α se averigua si la intersección existe y el segmento que la define.
Notar que β ∈ [0,1) , un intervalo semiabierto pues los vértices se cuentan sólo una vez. Hay que tener
cuidado con posibles errores de precisión: la recta no puede interceptar solamente una arista de un
triángulo a menos que coincida con la arista)
Cuando hay un mismo plano que intercepta (o
Qi (d’>0)
no) a muchos segmentos o triángulos o tetraedros
es mejor utilizar un algoritmo de level−sets. Se
calcula, para cada vértice una (pseudo)distancia
n
Iij
al plano {P0,n} y se buscar distancia 0 en las
aristas con extremos de distinto signo:
Qj (d’<0)
P0
d’i= |n|di = (Qi–P0)·n = Qi·n – P0·n
Notar que P0·n es constante.
Luego se interpola, buscando el valor 0, en cada
segmento o arista en la que cambie de signo entre
extremos:
d’i
0 − d’i
Iij = (1−α)Qi + αQj = Qi − d’ − d’ (Qj−Qi)
α = d’ − d’ ⇒
j
i
j
i
Circunferencias y Esferas
Aquí se presentan varios casos distintos. Podemos tratar de igual manera a la circunferencia en el
plano y a la esfera en el espacio; pero las circunferencias en el espacio (círculos o discos) se manejan
de un modo totalmente distinto. De la intersección general con discos, sólo diremos que hay que
calcular la intersección con el plano de soporte y verificar si es interior al círculo.
Para calcular la intersección entre una recta y una esfera (o circunferencia en el plano), se puede
plantear la ecuación de los puntos de la recta cuya distancia al centro sea igual al radio:
{C − [(1−α) P0 + α P1]}2 = r2 = [(C−P0) − α (P1−P0)]2
Poniendo el origen en P0 las ecuaciones se hacen más legibles. El resultado se traslada sumando P0.
(C − α P1)2 = r2 = C2 − 2αC·P1 + α2P12
⇒
P12 α2 − 2C·P1 α+ C2 − r2 =0
Dado que es una ecuación de segundo grado puede haber dos,
C┴ r’
una o ninguna solución. Para determinar el caso, hallamos el
2
n
discriminante y dividimos todo por P1 para ver que habrá
t
r
solución si:
P1
P0
∆ > 0 ⇒ C2 − (C·||P || )2 < r2 ⇒ C2 − (C·t)2 < r2
C
1
es decir, si la distancia del centro a la recta es
menor que el radio.
4/12
Un método alternativo, más sencillo y que sirve para todos los casos de circunferencias o esferas
contra rectas o planos consiste en calcular el pié de la perpendicular C⊥, verificar si esta dentro de la
esfera y luego calcular la intersección. Para hallar C⊥ utilizamos las ecuaciones deducidas antes para la
distancia del punto C a la recta o plano.
La misma figura muestra tres casos, que usan t o n:
a) Circunferencia y recta (P0,t) en el mismo plano.
b) Esfera y recta (P0,t) en el espacio, vemos el plano que forman la recta y el centro.
c) Esfera y plano (P0,n) en el espacio, vemos el plano de canto.
Todos esos casos se tratan igual por este método, como ya se explicó, se exceptúa sólo el caso del
disco contra una recta no coplanar.
Consideramos origen en P0 para simplificar. Se identifica primero el pié de la perpendicular desde el
centro a la recta o plano; como ya vimos, para la recta: C┴ = (C·t) t y para el plano: C┴ = C − (C·n) n.
Se compara luego el radio con la distancia entre C⊥ y C. Si hay intersección r’2 = r2 − (C┴ −C)2 define
la distancia a los dos puntos de intersección (C┴ ± r’ t) en la recta; o, si se trata de un plano contra una
esfera, r’ será el radio del disco de intersección, centrado en C┴ y en el mismo plano de normal n.
Nota: Usar como origen a P0 tiene sustento en que normalmente las rectas son rayos o semirrectas con
extremo en el punto de vista.
No podemos cubrir todos los casos y quedan varios que resultan útiles en CG, fundamentalmente las
intersecciones de rayos y planos con superficies paramétricas. Los métodos son siempre los mismos:
plantear de distintos modos las ecuaciones y elegir las simplificaciones y generalizaciones más
robustas. Como vimos, siempre hay que considerar si se trata de uno contra uno o de uno contra
muchos, en cuyo caso los métodos de optimización pueden obligar a usar técnicas distintas; por
ejemplo un rayo contra un triángulo o un rayo contra muchos triángulos o muchos rayos contra un
triángulo, en cada caso hay que analizar cual es la técnica más eficiente. Todos los casos de utilidad
están desarrollados e implementados en el libro de Buss: 3D Computer Graphics y con mucha mayor
extensión en el de Schneider y Eberly: Geometric Tools For Computer Graphic.
5/12
Optimización
La implementación de algoritmos geométricos debe hacerse con mucho cuidado para obtener las
prestaciones que se plantearon en la introducción de intersecciones. Primero se implementan las
ecuaciones tal como se deducen o se encuentran en la bibliografía, para verificar que el programa
funciona robustamente (siempre entrega un resultado útil) y con la precisión adecuada. Luego se puede
ajustar la eficiencia, sin perder los otros atributos, midiendo tiempos para miles o millones de
intersecciones, evitando utilizar algoritmos cuyo costo computacional en tiempo y memoria sea de
segundo orden o mayor en la cantidad de argumentos.
El mecanismo de optimización depende fuertemente del problema. El ejemplo mas importante de
intersecciones que se planteó aquí es el de rayo contra triángulo, puesto que la mayoría de los objetos
vienen dados mediante triangulaciones. En tal caso conviene averiguar en primer lugar si habrá
intersección, es decir si los parámetros correspondientes al triángulo estarán entre cero y uno. El
parámetro en el rayo se calcula solamente si se requiere la distancia al ojo (z-buffer) o, al menos,
averiguar si la intersección está delante del ojo. Por otro lado, también es muy frecuente el cálculo de
la intersección de un único plano con una gran cantidad de segmentos, por ejemplo cuando se corta un
objeto (sus aristas) mediante un plano para hacer clipping. En este caso se calcula el parámetro en el
segmento y solo cuando sepamos que habrá intersección; los parámetros en el plano no importan.
Las técnicas que veremos a continuación permiten el ordenamiento espacial y la simplificación de los
objetos para responder rápidamente a la pregunta: “¿puede haber intersección?”
Línea separadora y envoltorios
Dos objetos no se interceptan si sus proyecciones sobre alguna
línea no se solapan. Equivalentemente, si existe un plano que los
separe, dejando un objeto a cada lado.
Es muy sencillo proyectar muchos puntos en una línea, pero
encontrar una línea separadora puede ser más complicado e
ineficiente que calcular la intersección, por lo que se recurre a
proyecciones sencillas, por ejemplo las coordenadas (las líneas
son los ejes cartesianos); o la línea que une los centros.
Para los objetos complicados y los cóncavos se suele recurrir a envoltorios convexos simples. Separar
los envoltorios es más sencillo que separar los objetos. El análisis de intersecciones suele hacerse
primero con el envoltorio elegido, para luego analizar la intersección con el objeto.
CH
BS
AABB
OOBB
k−DOP
De izquierda a derecha, tenemos: el conocido convex−hull o mínimo envoltorio convexo; la esfera
envolvente o bounding−sphere o enveloping−sphere; el axis-aligned bounding−box o bounding−box a
secas, que podría traducirse como caja envolvente, es una caja ortogonal a los planos coordenados; el
oriented bounding−box o caja orientada, que puede estar definido por una dirección predefinida o por
los ejes principales del objeto (object−oriented bounding−box) y el k−discrete oriented polytope que
tiene k pares de direcciones de orientación. Todas tienen su extensión obvia a más de dos dimensiones.
El BB se calcula mediante los máximos y mínimos de cada coordenada. Los alineados (OBB y
k−DOP) con el máximo y mínimo calculado en un conjunto de direcciones (min_max(x·di)). La
mínima esfera, el menor OBB y el convex−hull son difíciles de calcular y requieren herramientas de
Geometría Computacional. Para juegos y Computación Gráfica en general, todos se pueden utilizar
aproximados y predefinidos al crear los objetos. El CH es especialmente útil cuando viene dado por
definición, por ejemplo en las curvas y superficies NURBS. La esfera provee la sencillez del cálculo
de sus intersecciones con otras o con rayos; es el envoltorio más sencillo y utilizado en juegos es la
6/12
esfera aproximada; ejemplos: La colisión o intersección entre dos objetos se descarta si los centros
están a mayor distancia que la suma de radios. La intersección de un objeto con un rayo se descarta si
el rayo dista del centro más que el radio.
Ordenamiento espacial
El análisis de intersecciones o de proximidad de puntos y objetos es esencialmente cuadrático: hay que
testear todos contra todos. Una rutina de orden cuadrático en el número de datos se puede hacer mucho
menos costosa si se subdivide el espacio en cajas (bins o buckets) que contienen unos pocos objetos y
se analiza el problema caja por caja. El paradigma de Divide and Conquer se basa en que la
∑pocos*pocos << todos*todos, normalmente ese principio se aplica recursivamente hasta el final (uno
contra uno) pero bien puede quedar en un estado intermedio de pocos contra pocos. El “mejor” método
para repartir objetos en cajas depende del problema; se pueden pre−ordenar los objetos, sus puntos o
sus envoltorios, dependiendo del problema en particular. El armado de las cajas se hace con estructuras
y algoritmos estándar y cada tipo de subdivisión está muy estudiado, solo se discute cual utilizar en
cada caso y ligeras variantes. Obviamente hay que considerar también el tiempo de división del
conjunto en cajas, el tiempo de armado de dicha estructura.
El ordenamiento más sencillo que puede pensarse es una simple subdivisión del espacio en cajas
idénticas. Normalmente entendemos por “espacio” el AABB del conjunto de objetos. Esta técnica
consiste en dividir cada coordenada en un número adecuado de partes. El principal problema aquí es la
gran cantidad de partes vacías; si la estructura queda muy desbalanceada (muy distinta cantidad por
celda) la reducción de tiempo no es muy grande. Una variante de éste método, que se utiliza en los
juegos en primera persona con recorridos por salas separadas, consiste en la obvia agrupación de
objetos en salas (más una relación de visibilidad a través de puertas y ventanas). Se denominan
métodos de cells and portals o celdas y portales.
Las mismas técnicas que se aprendieron para ordenamiento de números son generalizables para el
ordenamiento espacial, esa es casi una definición de Geometría Computacional (algoritmos y
estructuras de datos multidimensionales). En particular los árboles de divisiones recursivas reducen
mucho el costo algorítmico, en general a O(n log(n)) y la búsqueda de un elemento cercano es O(1).
Un primer refinamiento de la división en partes iguales consiste en subdividir recursivamente (cuatro
partes iguales en 2D u ocho en 3D) pero solo cuando la caja actual tiene más de determinada cantidad
de objetos o puntos. El método se denomina quadtree en 2D y octree en 3D.
Se puede utilizar una división más simple, que además puede extenderse mucho mejor a varias
dimensiones: el k-d tree, o árbol k-dimensional es una partición recursiva con un plano a la vez. Cada
plano puede partir a la mitad o por la mediana a la coordenada más larga de la celda o del BB de los
datos de la celda o simplemente ciclando (x, y, z, x, y, …) los planos cartesianos. Hay muchas
variantes, de acuerdo al método de selección y ubicación del plano de corte. Si los planos no están
alineados con los coordenados se denomina BSP-tree (binary space partition tree) y se utiliza con
mucha profusión en el ambiente de los desarrolladores de juegos.
División regular
Quadtree
k-d Tree
BSP Tree
7/12
Para el k-d-tree, se suelen ordenar los datos por coordenadas y partir con la mediana del conjunto de
cada celda. Esto produce árboles balanceados, es decir equilibrados en cantidad de elementos para
cada nivel de subdivisión, con ello se logran menos subdivisiones y menor profundidad total del árbol.
La selección del método y el balance costo/eficiencia dependen obviamente del problema particular.
Ejemplo: Algoritmo del Pintor mediante BSP-Tree. Se trata de realizar el renderizado en forma
ordenada desde el fondo hacia el frente, por ejemplo para objetos semitransparentes, aunque en general
se utiliza para determinar oclusión sin utilizar el z-buffer.
A
B
A
2
1
B
C
3
1
5
D
4
C
2
D
3
4
5
La explicación y el dibujo son bidimensionales, pero la técnica es exactamente igual en el espacio; el
divisor será un plano en lugar de una recta. No entraremos en los detalles complicadísimos de cómo
encontrar un divisor que no recorte objetos. En los juegos, esta construcción se hace en forma manual
para los objetos fijos, se hace una sola vez y se utiliza durante el desarrollo para el renderizado rápido.
A medida que se encuentra un divisor de los objetos restantes, éstos se asignan a cada lado del divisor,
construyendo un árbol de relaciones izquierda-derecha. Con el árbol construido (y probablemente
permanente) se indica, para cada divisor, de que lado está el observador. En la figura se indicó en rojo
la partición que contiene al observador en cada división. El orden de renderizado se obtiene
recorriendo el árbol en forma ordenada primero por donde no se encuentra el observador. La secuencia
de recorrido y renderizado es: A C 3 C D 4 D 5 D C A B 2 B 1 B A. Notar que el objeto 5 está más
cerca del ojo que el 2, pero aún así no puede ocluirlo, es decir que se recorren y renderizan primero, y
en forma completa, las ramas que no contienen al observador.
Ejemplo: Búsqueda del punto mas cercano con un k-d Tree.
En la figura el árbol parece estar construido utilizando los
puntos como divisores y admitiendo un solo punto interior en
cada hoja.
Por cada división del árbol se guardan: el BB, la coordenada
divisoria, el punto que la define, y un puntero a cada
subdivisión.
La búsqueda se realiza encontrando primero la hoja que
contiene al punto buscado. En cada rama se identifica de qué
lado de la subdivisión queda el punto y se pasa a la siguiente
hasta llegar a la hoja que lo contiene.
La hoja tiene un punto interior (o pocos), se busca el más
cercano y esa distancia define el radio de búsqueda posterior.
Ese radio define una circunferencia o, más sencillamente, un
cuadrado, que es su BB. Se busca, nuevamente en el árbol, en todas las hojas contenidas o que
interceptan a la circunferencia o su BB.
8/12
Diagrama de Voronoï y triangulación Delaunay
El diagrama de Voronoï es la última técnica de ordenamiento espacial que trataremos; pero le daremos
una atención más especial, debida a sus propiedades y múltiples aplicaciones.
En su forma más general consiste en dividir el espacio en celdas,
una para cada objeto; de modo que cada celda contiene los puntos
del espacio que están más cerca de su objeto que de cualquier otro.
Las múltiples variantes se deben al tipo de objetos y a la forma de
medir la distancia. Aquí estudiaremos sólo el diagrama de Voronoï
de puntos aislados y la distancia euclídea. El análisis lo haremos en
2D de un modo que permite analizar e implementar en 3D el mismo
procedimiento.
A los puntos dato (fijos) los llamaremos nodos, para diferenciarlos de los puntos comunes del espacio.
En la figura de arriba se muestra un conjunto de nodos y el diagrama de Voronoï. Todo el espacio se
divide en celdas convexas, cada una es el conjunto de puntos más cercanos a su nodo que a otro.
Para entender la geometría del problema tomamos un punto
cualquiera del plano y hacemos crecer una circunferencia centrada
en el punto. Si el punto está en el interior de alguna celda, la
circunferencia encuentra primero al correspondiente nodo, el más
cercano al punto. Si el punto está en una arista encuentra dos nodos
a la vez, la arista separa las dos celdas de los dos nodos equidistantes
del punto. Finalmente, si el punto es un vértice del diagrama, donde
se encuentran tres celdas, equidista de tres nodos a la vez.
Las aristas del diagrama de Voronoï separan dos celdas y equidistan de sus dos nodos. Forman parte de
la mediatriz de los dos nodos, que es la recta
que parte por la mitad y es perpendicular al
segmento que los une.
Los vértices, donde se juntan tres mediatrices,
son a su vez el centro de la circunferencia que
inscribe al triángulo formado por los tres
nodos. En 3D sucede lo mismo, las mediatrices
son planos y las circunferencias esferas.
El concepto y propiedad más importante es que un vértice del diagrama equidista de tres nodos y por
lo tanto es el centro de la circunferencia que inscribe al triángulo que forman. Lo mismo sucede en 3D
con esferas, cuatro nodos y el tetraedro que forman.
Los segmentos que unen a los nodos vecinos forman una triangulación. Aquí llamaremos triangulación
de un conjunto de nodos a una división de su convex-hull en triángulos
(o tetraedros en 3D, o símplices en general) de modo que:
1) Los nodos son vértices de los triángulos.
2) Dos triángulos comparten una arista completa o un nodo o nada
⇒ no hay uniones en T
3) Ningún triángulo tiene nodos en el interior.
⇒ Cada arista interior es compartida por dos triángulos.
⇒ No hay triángulos solapados
En la figura se puede notar que las celdas de nodos en el convex-hull son las únicas que tienen
extensión infinita. Esa característica se puede utilizar para determinar el CH del conjunto.
Dado el conjunto de nodos, hay muchas triangulaciones posibles. La triangulación que se obtiene
como “dual” del diagrama de Voronoï se llama Triangulación Delaunay.
Esa dualidad es un concepto extendido de la teoría de grafos. Cada vértice del diagrama es centro de la
circunferencia que equidista de los nodos y define el triángulo y se puede ver además la relación uno a
uno entre aristas (segmento - mediatriz) y entre celdas y nodos.
9/12
La siguiente tabla especifica en dos y tres dimensiones la dualidad de elementos.
Celda Voronoï
2D
Triángulo Delaunay
3D
Tetraedro Delaunay
Celda Voronoï
Celda
Arista
Vértice
Nodo
Arista
Triángulo
Celda
Arista
Cara
Nodo
Cara
Arista
Vértice
Tetraedro
Hay varios métodos propuestos y eficientes para construir un diagrama de Voronoï, o su equivalente
dual: la triangulación Delaunay. El método conceptualmente más sencillo aprovecha la característica
distintiva de la triangulación Delaunay: las circunferencias no contienen nodos en el interior.
La construcción se realiza agregando los nodos, de a uno, en una triangulación preexistente. Empieza
con un gran triángulo de nodos virtuales
(inexistentes) que envuelve a todo el conjunto.
Para cada nuevo nodo se buscan las
circunferencias que lo contienen, que deben ser
reemplazadas
por
otras
nuevas.
La
reconstrucción es local, se limita al entorno
natural (natural neighborhood) del nuevo nodo,
que es la unión de las circunferencias que lo
contienen. El conjunto de triángulos cuyas
circunferencias contienen al nuevo nodo forma
un polígono que envuelve al nodo y se
denomina “cavidad del nodo”, se reemplaza formando nuevos triángulos, cada uno con el nodo y una
arista exterior de la cavidad. En 3D la cavidad es un poliedro y el procedimiento es igual.
Cuando existen más de tres puntos “cocirculares” el diagrama de Voronoï tiene un vértice equidistante
de cuatro (o más) puntos. En tal caso, la triangulación genera problemas numéricos que se suelen
salvar perturbando la posición del nodo entrante, para restaurar la condición normal. En 3D el
problema es mucho mayor, porque la cocircularidad genera tetraedros aplastados conocidos como
slivers; hay una inmensa cantidad de técnicas publicadas para eliminarlos, pero es muy complicado.
El diagrama de Voronoï se obtiene naturalmente en procesos
de crecimiento que parten desde “semillas” fijas, Puede verse
en el caparazón de una tortuga, en el crecimiento de granos
apiñados o en el crecimiento de cristales en las aleaciones.
En la figura se muestra construido como una intersección de
conos vista desde arriba. Los conos simulan el crecimiento a
velocidad constante desde los nodos (crece el diámetro a
medida que aumenta la profundidad). Como método
constructivo es extremadamente ineficiente, pero para unos
pocos nodos, podemos visualizar el diagrama con unas pocas
líneas de código en OpenGL.
El diagrama de Voronoï y la triangulación Delaunay tienen propiedades muy fructíferas en
computación gráfica y geométrica, debido a que codifican naturalmente las relaciones de proximidad y
vecindad que, de otro modo, serían muy costosas de construir. Sobran ejemplos. Podemos averiguar en
forma muy eficiente cuales son los nodos cercanos a un determinado punto, averiguando a que
triángulo pertenece. Podemos planear el movimiento automático de un robot, esquivando objetos de la
escena, si lo obligamos a moverse por las líneas del diagrama de Voronoï. ¿Donde conviene poner una
nueva farmacia? En el diagrama de Voronoï de las farmacias existentes, elegimos el centro de la
circunferencia más grande, que es un vértice del diagrama.
10/12
Búsqueda lineal o linear walk
Para muchas operaciones de búsqueda de proximidad y en particular para la construcción incremental
del diagrama de Voronoï, se requiere saber a que esferas o círculos pertenece un punto (el nuevo nodo
a insertar) y podemos averiguarlo respondiendo a que tetraedro o triángulo pertenece. El proceso más
eficiente para hacerlo se denomina linear walk.
Tenemos una triangulación (no necesariamente Delaunay pero si convexa) de un conjunto de nodos y
queremos averiguar a que triángulo pertenece un punto del plano. El procedimiento consiste en partir
de un triángulo cualquiera y movernos por vecindades, de un modo recursivo que nos acerque cada vez
más al punto. Para ello debemos contar con una estructura de datos que identifique, para cada
triángulo, cuales son sus vecinos (por arista en 2D; por cara de tetraedros en 3D), ordenamos la lista de
modo que el vecino i-ésimo sea opuesto al i-esimo nodo del triángulo (i ∈ {0,1,2}). Podemos asignar
el puntero nulo al exterior del CH en las aristas de frontera.
1
α0 < 0
2
0
0 < α0 < 1
α0 > 1
1
2
0
Siguiendo la figura anterior, partimos del triángulo pintado y calculamos las coordenadas baricéntricas
en el punto. Sabemos que la línea del segmento opuesto a cada vértice separa el semiplano positivo del
negativo. La coordenada baricéntrica más negativa nos indica entonces a que vecino pasar.
Hay que aclarar que el nodo más cercano al punto no es necesariamente alguno de los nodos del
triángulo pero si debe estar entre los que definen las circunferencias que contienen al punto. Las
circunferencias se hallan buscando entre los vecinos de cada una hallada, empezando por el triángulo
que contiene al punto.
Cuando hay muchísimos triángulos, el proceso de búsqueda lineal se acelera si se precalcula una
estructura de ordenamiento espacial para el conjunto de nodos, puede ser un quadtree o un k-d-tree. Si
se colocan unos pocos nodos por celda terminal, basta incorporar el punto buscado en la estructura y
partir desde algún triángulo de un nodo de la misma celda terminal u hoja del árbol.
Otro mecanismo de aceleración se usa cuando se barren píxeles o vóxeles en imágenes o tomografías,
en tal caso conviene empezar la búsqueda por el triángulo que contenía al píxel anterior vecino. Muy
probablemente, el actual esté en el mismo y si no, en un vecino.
Cuando se posee cualquier tipo de polígonos o poliedros, no necesariamente simpliciales (triángulos o
tetraedros) el proceso de búsqueda se puede realizar también buscando una cara o lado que intercepte
el rayo que une un punto interior del polígono con el punto buscado. El ejemplo más común es ubicar
en que sala está el personaje móvil en un juego, o que sala señala el jugador con el cursor.
11/12
Circunferencia de tres puntos, esfera de cuatro…
En el proceso de armado del diagrama de Voronoï, se crean y destruyen esferas o circunferencias con
cada punto incorporado, por lo tanto el algoritmo utilizado para definirlas debe implementarse con la
mayor eficiencia y robustez posibles. El análisis siguiente es válido en cualquier cantidad de
dimensiones, pero fijemos ideas en 2D.
Queremos el centro C y radio r de la circunferencia definida por los tres
P1
puntos {P0, P1, P2}. La ecuación que los define plantea la distancia al
centro, común para todos los puntos:
r2 = (C−Pi)2 = C2 − 2 C·Pi + Pi2
En 2D son tres ecuaciones (i ∈ {0,1,2}) y tres incógnitas (Cx, Cy, r2),
C
P2
pero cuadráticas. Para librarnos de C2 ponemos el origen en P0, lo que
r
equivale a restar P0 a cada punto. La primera ecuación queda:
r2 = (C−P0) 2 = C2, (el modulo del vector r indicado en el dibujo)
P0
reemplazando r2 en las siguientes ecuaciones queda:
C2 = C2 − 2 C·Pi + Pi2 ⇒ 2 C·Pi = Pi2 (i ∈ {1,2})
De ese sistema lineal 2x2 (o dim x dim en más dimensiones) se calculan C y su módulo r, luego se
ubica C en el sistema original sumando P0.
El determinante de los coeficientes es un múltiplo del área del triángulo (volumen del tetraedro, etc.).
Si se buscan las coordenadas baricéntricas αi de C, se puede suponer origen en P0 y los dos Pi como la
base del sistema, queda:
2gjk αj Pik = 2gjk αj δik = 2gji αj = 2αj (Pi·Pj) = Pi2 (i,j,k ∈ {1,2})
Reordenando la ecuación original, en el sistema original:
Pi2 = 2 C·Pi + r2 − C2,
el primer miembro equivale a “subir” los puntos a un paraboloide de revolución en una dimensión más y
el segundo miembro es un plano de normal 2C y término independiente r2 − C2. La intersección de ambos, proyectada de
nuevo, es la circunferencia. Si P{x,y} representa cualquier punto del plano, w = P2 = x2 + y2 es un paraboloide en una
dimensión más. Toda la triangulación Delaunay coincide con la proyección del convex−hull del conjunto de puntos subidos
al paraboloide y de hecho esa lifting transformation se suele utilizar para construirla y, en general, es un mecanismo muy
utilizado para linearizar ecuaciones geométricas de segundo grado. Es parecido al tratamiento de linearización que provee
el espacio proyectivo. Por ejemplo, un punto está dentro de la circunferencia si su versión subida (lifted) al paraboloide está
debajo del plano, esto se reduce a calcular el signo del determinante (triple producto escalar) que define la distancia del
punto al plano. No hace falta calcular la circunferencia, el signo del determinante discrimina si el punto está dentro o fuera.
Néstor Calvo
Computación Grafica
FICH - UNL
12/12