FUNCIÓN LOGARÍTMICA
Anuncio

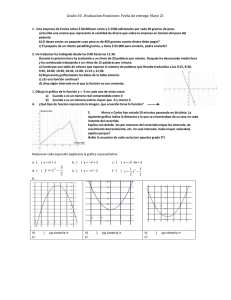
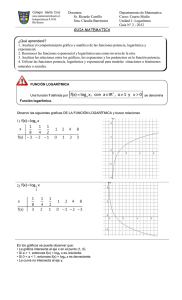
FUNCIÓN LOGARÍTMICA. Las funciones inversas a las funciones exponenciales se denominan logarítmicas. El término logaritmo proviene de las raíces griegas logos y arithmos, y viene a significar “números para calcular”. Durante siglos fueron instrumento esencial a la hora de realizar cálculos complicados. La regla de cálculo, hoy desplazada por las calculadoras electrónicas, se basaba en ellos. Los logaritmos varían muy lentamente, lo que les hace ser escala numérica adecuada para medir fenómenos naturales que implican números muy grandes, tales como la intensidad del sonido, la de los movimientos sísmicos, la datación de restos arqueológicos, etc. DEFINICIÓN DE FUNCIÓN LOGARÍTMICA. Una función logarítmica es aquella que se expresa como y= f (x) = logax, siendo a la base de esta función, que ha de ser positiva y distinta de 1. PROPIEDADES DE LA FUNCIÓN LOGARÍTMICA. Las propiedades generales de la función logarítmica se deducen a partir de las de su inversa, la función exponencial. Así, se tiene que: • • • • La función logarítmica sólo existe para valores de x positivos, sin incluir el cero. Por tanto, su dominio es x>0 Las imágenes obtenidas de la aplicación de una función logarítmica corresponden a cualquier elemento del conjunto de los números reales ℜ ( -∞ , +∞) En el punto x = 1, la función logarítmica se anula, ya que loga 1 = 0, en cualquier base. Finalmente, la función logarítmica es continua y es creciente para a > 1 y decreciente para a < 1. LOGARITMO DE UN NÚMERO. El logaritmo de un número N, con base a, es el exponente x a que hay que elevar la base para obtener dicho número. En la expresión logaN= x, N es el número dado y x es el logaritmo de dicho número. De acuerdo a la definición de logaritmo, las expresiones: y= logax y ay=x son equivalentes. Para que se comprenda mejor este concepto habrá que analizar los siguientes ejemplos. Base 2 2-3=1/23=1/8 2-2=1/22=1/4 2-1= 1/21=1/2 20=1 21=2 22=(2)(2)=4 23=(2)(2)(2)=8 24=(2)(2)(2)(2)=16 25=(2)(2)(2)(2)(2)=32 Logaritmo log2 1/8=-3 log2 1/4=-2 log2 1/2=-1 log2 1=0 log2 2=1 log2 4=2 log2 8=3 log2 16=4 log2 32=5 Base 4 Logaritmo 4-3=1/43=1/64 4-2=1/42=1/16 4-1= 1/41=1/4 40=1 41=4 42=(4)(4)=16 43=(4)(4)(4)=64 44=(4)(4)(4)(4)=256 45=(4)(4)(4)(4)(4)=1024 log4 1/64=-3 log4 1/16=-2 log4 1/4=-1 log4 1=0 log4 4=1 log4 16=2 log4 64=3 log4 256=4 log4 1024=5 El log216=4, porque el logaritmo representa el exponente al que hay que elevar la base 2 para obtener el número 16. Base 5 5 =1/5 =1/125 5-2=1/52=1/25 5-1= 1/51=1/5 50=1 51=5 52=25 53=125 54=625 55=3125 -3 3 Logaritmo log5 1/125=-3 log5 1/25=-2 log5 1/5=-1 log5 1=0 log5 5=1 log5 25=2 log5 125=3 log5 625=4 log5 3125=5 Base 10 10 =1/103=1/1000 10-2=1/102=1/100 10-1= 1/101=1/10 100=1 101= 10 102= 100 103= 1000 104= 10000 105= 100000 -3 Logaritmo log 1/1000=-3 log 1/100=-2 log 1/10=-1 log1=0 log10=1 log100=2 log1000=3 log10000=4 log100000=5 Nota. Cuando la base es 10 ésta no se escribe. El log1000=3, porque el logaritmo representa el exponente al que hay que elevar la base 10 para obtener el número 1000. Cualquier número positivo diferente de 1 puede ser utilizado como base para construir un sistema de logaritmos. Sin embargo, los sistemas de logaritmos más utilizados son los de base 10 y el de base e ( e=2.7182). El sistema de logaritmos que usa la base 10 se conoce como logaritmos vulgares o de Briggs (log), y el de base e como logaritmos naturales o Neperianos (ln). GRÁFICAS DE FUNCIONES LOGARÍTMICAS. Ejemplo 1. Construir la gráfica de la función logarítmica y=f(x)=log x. x 1/1000 1/100 1/10 1 4 10 100 y=f(x)= log x log 0.001= -3 log 0.01= -2 log 0.1= -1 log 1= 0 log 4= 0.6020 log 10= 1 log 100= 2 (x,y) (0.001, -3) (0.01, -2) (0.1, -1) (1, 0) (4, 0.620) (10, 1) (100, 2) La gráfica de la función y=f(x)= f(x)=log x es la siguiente. y x Dominio D= Reales positivos x>0 Rango R= Todos los reales ℜ ( -∞ , +∞) ¿Es una función inyectiva, sobreyectiva o biyectiva? Biyectiva. Porque cumple con ser inyectiva y sobreyectiva, por tanto es biyectiva. Ejemplo 2. Construir la gráfica de la función logarítmica y=f(x)=log4 x, su expresión equivalente es x=4y. x 1/64 1/16 1/4 1 4 16 64 256 y=f(x)= log4 x log4 1/64= -3 log4 1/16= -2 log4 1/4= -1 log4 1= 0 log4 4= 1 log 4 16= 2 log 4 64= 3 log 4 256= 4 (x,y) (1/64, -3) (1/16, -2) (1/4, -1) (1, 0) (4, 1) (16, 2) (64, 3) (256, 4) x Dominio D= Reales positivos x>0 Rango R= Todos los reales ℜ ( -∞ , +∞) ¿Es una función inyectiva, sobreyectiva o biyectiva? Biyectiva. Porque cumple con ser inyectiva y sobreyectiva, por tanto es biyectiva.