The MATLAB Notebook v1.6

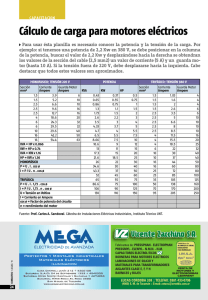
Cálculo de caídas de tensión
Transporte de energía eléctrica 28/10/10
En la red trifásica, de MT de la figura, la tensión de alimentación en el nudo A, es de 21 kV, el
tipo de conductor es LA56. Calcular la tensión en la carga de 550 KVA cos(fi)=0.95 (i),
sabiendo que la reactancia es de 0,4 ohms/km.
350 m
550 m
450 m
400 m
A
250 kW
cos(fi) =0.85 (i)
400 kW
cos(fi)=0.85 (i)
550 kW
cos(fi) =0.95 (i)
clear
l=[350,550,450,400];%vector de longitudes de cada tramo en m
Sc=[250,400,550,600;0.85,0.85,0.95,0.9;j,j,j,j];% kW, cos_fi,tipo
S=Sc(1,:).*exp(acos(Sc(2,:)).*Sc(3,:))./Sc(2,:);
U=21;%21 kV: inicial U1=U2=U3=U4=U;
R=0.614;%Ohmios/km a 20 ºC LA56
X=0.4;% Ohmios/km
zu=R+j*X;%impedancia por km
Z=l.*zu/1000;
Ub=20;%20 kV
Sb=1000;%1000 kVA
Zb=Ub^2/Sb*1e3;% por estar Ub en kV y Sb en kVA
Ib=Sb/Ub/sqrt(3);
zl=Z/Zb;
s=S./Sb;ua=U/Ub;
u=ones(1,4)*ua;%inicializar: todas las tensiones iguales
error=1;n=1;
while error >1e-7&n<10
I=conj(s./u);%intensidades en función de u
for k=1:length(I)
if k==1
u(k)=ua-zl(k)*sum(I);
else
u(k)=u(k-1)-zl(k)*sum(I(k:length(I)));
end
end
error=max(s-u.*conj(I));
n=n+1;
end
I_tramos=[sum(I),sum(I(2:4)),sum(I(3:4)),I(4)];
Pot_entr_al_sist_en_ori= 3*U/ sqrt(3)*conj(sum(I*Ib));% en kVA
Perdidas_totales= Pot_entr_al_sist_en_ori-sum(S);% en kVA
error=Perdidas_totales-sum(Z.*abs(I_tramos*Ib).^2)*3/1e3
error =
-6.8624e-005 -4.4702e-005i
600 kW
cos(fi) =0.9 (i)
Cálculo de caídas de tensión
Transporte de energía eléctrica 28/10/10
1º.-En la red trifásica de MT de la figura, la tensión de alimentación en el nudo A es de 20,5 kV.
El conductor es LA110, la reactancia media es de 0,385 ohms/km y la resistencia de 0,307
ohmios/km.
450 m
350 m
250 m
600 m
A
B1
600 kVA
cos(fi) =0.85
(i)
250 kVA
cos(fi) =0.90
(i)
250 kVA
cos(fi) =0.975
(i)
600 kVA
cos(fi) =0.95
(i)
Calcular:
las tensiones en las cargas.
las caídas de tensión en cada tramo
las pérdidas de potencia
verificar que, las pérdidas totales son la suma de las pérdidas de cada tramo.
2º.-La línea trifásica de doble circuito tiene 275 km, sus conductores están dispuestos según
se indica en la siguiente figura figura:
A1
C2
9m
7,5 m
15,75 mm
B1
B2
12 m
7,5 m
C1
A2
Cálculo de caídas de tensión
Transporte de energía eléctrica 28/10/10
Los conductores son cables de Aluminio-Acero con las siguientes características
- Composición
30 Al + 7 Acero
- Diámetro exterior
15.75 mm
- Resistencia en c.a
0.154 / km
A
La tensión en origen de línea es 220 kV y la demanda de potencia en final 175 MVA, factor
de potencia 0.95 lnductivo. (Valores de base : Sb = 200 MVA , Ub = 220 kV)
Deterninar:
1. Los parámetros de la línea.
2. La impedancia y el ángulo característicos.
3. La tensión en fin de línea.
4. La caída de tensión y las pérdidas de potencia.
3º.-Una línea trifásica de cobre con 70 mm2 de sección y 45 m de longitud, alimenta un
cuadro cuyo consumo global es de 95 A con factor de potencia 0,9 inductivo. La
resistividad es de 0,0175 Ωmm2/m.
Hallar:
la caída de tensión que se produce en la línea.
la pérdida de potencia.
A
A
Cálculo de caídas de tensión
Transporte de energía eléctrica 28/10/10
1º.-En la red trifásica, de MT de la figura, la tensión de alimentación en el nudo A, es de 20,5
kV, el tipo de conductor es LA180. La reactancia es de 0,39 ohms/km y la resistencia de
0,1962 ohmios/km.
550 m
600 m
450 m
800 m
A
400 kVA
cos(fi) =0.90
(i)
1250 kVA
cos(fi) =0.85
(i)
650 kVA
cos(fi) =0.975
(i)
1000 kVA
cos(fi) =0.95
(i)
Calcular:
las tensiones en las cargas.
las caídas de tensión en cada tramo.
las pérdidas de potencia y el rendimiento de la distribución.
verificar que, la suma de las pérdidas de cada tramo es igual a las pérdidas totales.
2º.-Una línea trifásica de 250 km tiene sus conductores dispuestos según se indica en la
figura. La tensión en fin de línea es 400 kV y la carga es 250 MVA con factor de potencia
0.95 inductivo. Aplicar una base de 300 MVA y 400 kV.
0,3 m
A
8m
30,42 mm
C
4m
B
3m
9m
Cálculo de caídas de tensión
Transporte de energía eléctrica 28/10/10
Los conductores son cables de Aluminio-Acero con las siguientes características
- Composición
54 Al + 7 Acero
- Diámetro exterior
30.42 mm
- Resistencia en c.a
0.062 / km
B
Determinar:
1. Los parámetros de la línea: inductancia, resistencia y susceptancia capacitiva.
2. La impedancia y el ángulo característicos.
3. La tensión en origen de línea.
4. La caída de tensión y la pérdida de potencia en la línea.
5. La tensión en origen, aplicando la suma de las tensiones incidente y reflejada.
3º.-Una línea trifásica de cobre con 50 mm2 de sección y 45 m de longitud, alimenta un
cuadro cuyo consumo global es de 60 A con factor de potencia 0,95 inductivo. La
resistividad es de 0,0175 Ωmm2/m.
Hallar:
la caída de tensión que se produce en la línea.
la pérdida de potencia.
B