pequeñas diferencias

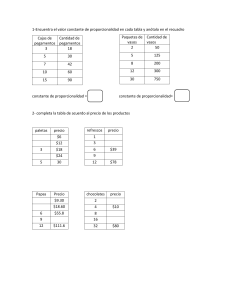
PEQUEÑAS DIFERENCIAS,
GRANDES DESPROPORCIONES
la situación
Aquí tienes dos cuerdas de 80 y 40 cm. Como ves, la primera es doble de la segunda. Corta
en cada cuerda un trozo de 20 cm. A simple vista, sin tomar ninguna medida, ¿crees que
sus longitudes de ahora son proporcionales a las de antes, o sea, siguen siendo doble una
de la otra?
80 cm
40 cm
Aquí tienes cuatro rectángulos. A simple vista, sin tomar ninguna medida, ¿crees que los
rectángulos son semejantes?
Grupo Azarquiel
el problema
☞Sumar (o restar) una misma cantidad a dos longitudes distintas altera la proporción que
existía entre ellas.
☞Si añadimos (o quitamos) la misma cantidad a cada uno de los lados de un rectángulo, el
rectángulo que se obtiene no es semejante al primero.
☞En cambio, si multiplicamos o dividimos por un mismo número dos longitudes o los
lados de un rectángulo, sí se mantienen las mismas proporciones que en las figuras
primitivas. Esto lleva a generalizar incorrectamente la propiedad a los casos anteriores
de suma y resta.
☞Los ejemplos que se utilizan para presentar estos conceptos suelen mantener siempre la
proporcionalidad lo que impide ver que hay otras muchas situaciones en las que la
proporcionalidad no es cierta.
sugerencias didácticas
☞Abordar el concepto de proporcionalidad desde distintas perspectivas (numérica,
geométrica, medida…) que conduzcan a ella.
☞Llegar a este concepto después de conocer las propiedades geométricas de las figuras y
de tener cierta destreza con los diferentes tipos de números.
☞Utilizar muchas y variadas actividades relacionadas con la vida cotidiana, en las que se
presente la proporcionalidad.
☞No reducir el estudio de la proporcionalidad numérica a situaciones mecanizadas de
“regla de tres”.
☞No reducir el estudio de la proporcionalidad geométrica al estudio del Teorema de
Tales.
☞Presentar siempre relaciones no proporcionales frente a relaciones proporcionales.
Grupo Azarquiel