El objetivo que debemos buscar para resolver ecuaciones de primer grado con una sola incógnita es ir haciendo
operaciones para dejar la incógnita en un lado de la igualdad y todos los demás términos en el otro lado. De esta
forma, al final obtendremos el valor de la incógnita.
Cuando pasamos un término de un lado a otro de la igualdad debemos pasarlo haciendo la operación opuesta a la que
esté realizando. Si está sumando, pasa restando, si está multiplicando pasa dividiendo, etc.
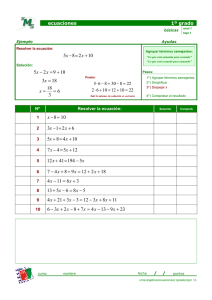
+ 1 = 3(5 − 2 ) en primer lugar hacemos las operaciones
+ 1 = 15 − 6 Ahora pasamos -6x y +1, al otro lado. Como +1 está sumando pasa restando y -6x está restando,
pasa sumando
+ 6 = 15 − 1
7 = 14 Ahora, el 7 lo pasamos al otro lado, como está multiplicando, pasa dividiendo.
=
= 2 Ya está resuelta. Ya hemos calculado el valor de x. Si queremos comprobarlo, sólo tenemos que coger la
ecuación y donde pone x poner 2 y ver si la igualdad se cumple
+ 1 = 3(5 − 2 )
2 + 1 = 3(5 − 2 ∗ 2)
3 = 3 ∗ (5 − 4)
3 =3∗1
3=3
Como podemos comprobar, la igualdad se cumple.
Ahora el resto de ecuaciones, las hago paso a paso, pero sin escribir las explicaciones.
3 − 5 + 2 + 3 = −12
3 + 2 = −12 − 3 + 5
5 = −10
=
= −2
3(2 − 5) − 2 = 10 + 9
6 − 15 − 2 = 10 + 9
6 − 2 − 9 = 10 + 15
−5 = 25
= = −5
3
3
3
+ 2 = 14
= 14 − 2
= 12
= =4
= √4 = 2
Esta es una ecuación de segundo grado completa del tipo
±√
+
+ = 0, se resuelve por medio de la ecuación
general para resolver ecuaciones de este tipo: =
(2 − 1) + 1 = 26
4 − 4 + 1 + 1 = 26
4 − 4 + 2 − 26 = 0
4 − 4 − 24 = 0 podemos simplificarla, dividiendo todo por 4. Quedaría así
− −6 =0
En esta ecuación:
“a” coeficiente de
=1
“b” coeficiente de = −1
“c” término independiente = 6
Sustiuimos los datos en la fórmula
=
(
)± (
)
∗ ∗(
∗
Tiene 2 soluciones:
=
= =3
=
=
= −2
)
=
±√
=
±√
=
±