3. Pulsos representativos

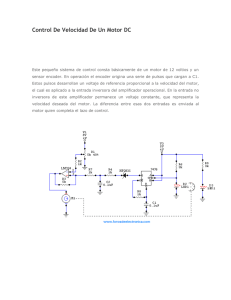
Propagación lineal de pulsos en fibra óptica
3. Pulsos representativos
3.1 Pulsos gaussianos
Como su propio nombre indica son pulsos cuya envolvente es una gaussiana. Los
pulsos gaussianos tienen solución analítica conocida. Para nuestras simulaciones dichos
pulsos irán multiplicados por una portadora por lo que realmente los pulsos que usaremos
serán de la forma
U (0, t ) = A(0, t ) × e jω 0t
Y la envolvente para el caso particular del pulso gaussiano será:
t ⎤
⎡ 1
A(0, t ) = Ao exp⎢− (1 + iC )·( )⎥
To ⎦
⎣ 2
Si lo representamos gráficamente:
Figura 12
Pulsos gaussianos chirpeados
Los pulsos gaussianos, como vimos en el apartado anterior, son pulsos cuya
envolvente es una función gaussiana, y cuando la frecuencia del pulso varía con el tiempo se
dice que tienen chirp. Las razones por la que se suele emplear esta familia de pulsos en el
estudio de la dispersión son:
- Por conveniencia matemática, puesto que la transformada de Fourier de un pulso
gaussiano es también un pulso gaussiano.
- Porque los pulsos emitidos por los láseres fabricados con semiconductores, cuando
se modulan directamente, adquieren un cierto chirp.
- Porque tanto la dispersión como algunos efectos no lineales pueden provocar que
pulsos que inicialmente no tienen chirp lo adquieran al propagarse por la fibra.
Propagación lineal de pulsos en fibra óptica
La expresión matemática del pulso gaussiano es:
t ⎤
⎡ 1
A(0, t ) = Ao exp⎢− (1 + iC )·( )⎥
To ⎦
⎣ 2
Donde A0 es la amplitud de pico del pulso, T0 determina la anchura, y C es el factor
de chirp, que determina el grado de variación de la frecuencia del pulso. Como vemos en la
ecuación anterior, variaciones cuadráticas en la fase den lugar a variaciones lineales en
frecuencia. Si C es positivo, la frecuencia del pulso aumenta linealmente con el tiempo, y si
C es negativo, disminuye linealmente con el tiempo. A continuación se puede ver la
representación gráfica de un pulso gaussiano con chirp negativo:
Figura 13: Amplitud de un pulso gaussiano con factor de chirp C=-3
Como vemos en la gráfica la frecuencia del pulso va variando linealmente por eso
decimos que el pulso esta linealmente chirpeado.
El espectro en frecuencia de un pulso chirpeado es siempre mayor que el de uno no
chirpeado de la misma longitud. Esto es fácil de demostrar si trasformamos al dominio de la
frecuencia la ecuación del apartado anterior:
⎛ 2·π ·To 2
A(0, ω ) = Ao⎜⎜
⎝ 1 + iC
1
⎡ ω 2 To 2 ⎤
⎞2
⎟⎟ exp ⎢−
⎥
⎠
⎣ 2(1 + iC ) ⎦
Como se observa, la anchura espectral viene dada por:
Δω o = 1 + C 2 / T o
En ausencia de chirp (pulso gaussiano normal) la anchura espectral satisface la
relación ΔωoTo = 1 . Es decir, la anchura espectral de un pulso gaussiano chirpeado es igual a
la de uno no chirpeado multiplicado por un factor:
1+ C 2
Propagación lineal de pulsos en fibra óptica
Si queremos calcular analíticamente como evoluciona el pulso a lo largo de la fibra,
multiplicamos en frecuencia por la ecuación de la fibra y calculamos la antitransformada:
A(ξ , t ) =
⎡ (1 + iC 1) i
⎛ ξ
+ tan −1 ⎜⎜
exp ⎢−
2
2
2
bf
⎝ 1 + Cξ
⎣ 2To bf
Ao
⎞⎤
⎟⎟⎥
⎠⎦
Donde ξ es la distancia normalizada y vale ξ = z / Ld , siendo Ld la longitud de
dispersión (longitud a la que la dispersión comienza a ser significativa) y que tiene un valor:
Ld = To 2 / β 2 . El parámetro bf (factor de anchura) y C1 (chirp instantáneo están
relacionados con ξ de la forma:
[
bf (ξ ) = (1 + sC ξ ) 2 + ξ 2
]
1
2
C 1(ξ ) = C + s (1 + C 2 )ξ
Donde s=signo de β 2 que toma un valor + o – dependiendo de si el pulso se
propagaba en la zona de dispersión normal o anómala de la fibra.
El código para representar en matlab dichas ecuaciones seria:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%
%%%
%%% NOMBRE DEL ARCHIVO: Chirp.m
NOMBRE DE LA FUNCION: Chirp %%%
%%%
%%%
%%% AUTOR: Francisco Cerezo Dominguez
FECHA:09-4-2006
%%%
%%%
%%%
%%% DESCRIPCION: La funcion calcula el ensanchamiento producido
%%%
%%%
en un pulso gaussiano chirpeado de To=50 ps cuando
%%%
%%%
se propaga en tercera ventana por una fibra optica
%%%
%%%
en funcion de la distacia normalizada (previamente
%%%
%%%
definida). Despreciamos los efectos de atenuación
%%%
%%%
y el retardo de grupo (primera derivada).
%%%
%%%
%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function Chirp
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% DATOS %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% longitud de onda de trabajo (nm)
lambda=1550;
% c (nm/ps)
c=3*10^5;
% lambda a la que la dispersion es 0 (nm)
lambdao=1312;
% pendiente de la dispersion en lambdao en ps/nm^2*Km
So=0.090;
Propagación lineal de pulsos en fibra óptica
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Anchura del pulso gaussiano To picoseg
To=50; %ps
% Calculamos B2 (ps^2/Km)
Dispersion=(So/4)*(lambda-(lambdao^4)/(lambda^3));
B2=-(Dispersion*(lambda^2))/(2*pi*c)
% Vamos a representar los datos que obtuvimos en teoria
% Definimos el vector de distancias
z=[0:1/100:300];
% Calculamos la distancia Ld
Ld=(To^2)/abs(B2);
Dnorm=z/Ld;
s=sign(B2);
% Definimos las tres funciones a representar
% Chirp igual a 2
chirp=2;
anchura1=sqrt((1+s*chirp*Dnorm).^2+(Dnorm.^2));
C1=chirp+s*(1+chirp^2)*Dnorm;
% Chirp igual a -2
chirp=-2;
anchura2=sqrt((1+s*chirp*Dnorm).^2+(Dnorm.^2));
C2=chirp+s*(1+chirp^2)*Dnorm;
% Chirp igual a 0
chirp=0;
anchura3=sqrt((1+s*chirp*Dnorm).^2+(Dnorm.^2));
C3=chirp+s*(1+chirp^2)*Dnorm;
% Representamos las gráficas
figure(1);
plot(Dnorm, anchura1)
hold on
plot(Dnorm, anchura2,'r')
plot(Dnorm, anchura3,'g')
hold off
figure(2);
plot(Dnorm, C1)
hold on
plot(Dnorm, C2,'r')
plot(Dnorm, C3,'g')
hold off
Si representamos gráficamente los las dos expresiones anteriores obtedremos:
Propagación lineal de pulsos en fibra óptica
Figura 14
Hemos llegado a estos resultados mediante el desarrollo analítico de las ecuaciones
correspondientes, pero el objeto de nuestro proyecto es llegar a estas soluciones, mediante la
simulación de la propagación de pulsos chirpeados a través de una fibra, dejando un lado
este desarrollo matemático que simplemente se muestra aquí como anexo aclaratorio.
3.2- Pulsos supergaussianos
En los sistemas de telecomunicaciones reales las envolventes de los pulsos de luz
generados por los láseres existentes no se corresponden exactamente con los pulsos
gaussianos normales o los pulsos gaussianos chirpeados. Para caracterizar la envolvente de
los pulsos que emiten estos dispositivos haremos uso de los mencionados pulsos
supergaussianos:
La ecuación matemática que describe un pulso supergaussiano es:
⎡ 1 + jC ⎛ t ⎞ 2 m ⎤
A(0, t ) = Ao exp ⎢−
⎜ ⎟ ⎥
2 ⎝ To ⎠ ⎥⎦
⎢⎣
Y la forma genérica del pulso una vez multiplicado por la portadora sería:
Figura 15
Propagación lineal de pulsos en fibra óptica
Donde el parámetro m controla la forma del pulso. El pulso se asemejará más a un
pulso rectangular cuanto más alto sea el valor de m. Los pulsos gaussianos chirpeados se
corresponden con valores de m=1. Para valores altos de m el pulso se asemeja a un pulso
rectangular.
En el apartado de simulación estudiaremos la propagación de un pulso que tenga por
envolvente a un pulso supergaussiano para algunos valores de m.