Fuerza de Lorentz

1 de 2
Física 2º Bach. – Acción del campo magnético sobre cargas en movimiento
1.- Fuerza de Lorentz
- Es la fuerza que ejerce el campo magnético sobre partículas cargadas en movimiento relativo al campo. Si la
carga se expresa en Culombios, la velocidad se expresa en m/s y el campo en Teslas, la fuerza se obtendrá en
Newtons.
⃗ = q (⃗v ∧ ⃗
F
B)
(*) El sentido de
{
⃗
∣F∣=Q
v B sen(α) , siendo Q=∣q∣
Sentido :regla del tornillo (*)
}
( N , C , m/s , T )
⃗ se obtiene girando ⃗v hacia ⃗
⃗v ∧ B
B por el camino más corto.
(*) Si la carga q es positiva la Fuerza tendrá el mismo sentido que
⃗
⃗v ∧ B
(*) Si la carga q es negativa la Fuerza tendrá el sentido opuesto a
⃗
⃗v ∧ B
- Si la velocidad y el campo son perpendiculares, la partícula describirá una trayectoria circular con velocidad
angular constante. El radio de la trayectoria y la velocidad de la partícula se obtienen aplicando la 2ª Ley de
Newton y dependen de la importante relación carga/masa.
v2
mv
=q v B⇒ R=
R
QB
v BQ
ω= =
R
m
m
- Cuando actúan sobre la partícula, de forma conjunta, un campo magnético y uno eléctrico, la expresión de la
Fuerza total es la siguiente (suma de las fuerzas magnética y eléctrica) :
F⃗T = q(⃗
v∧⃗
B)+q ⃗
E
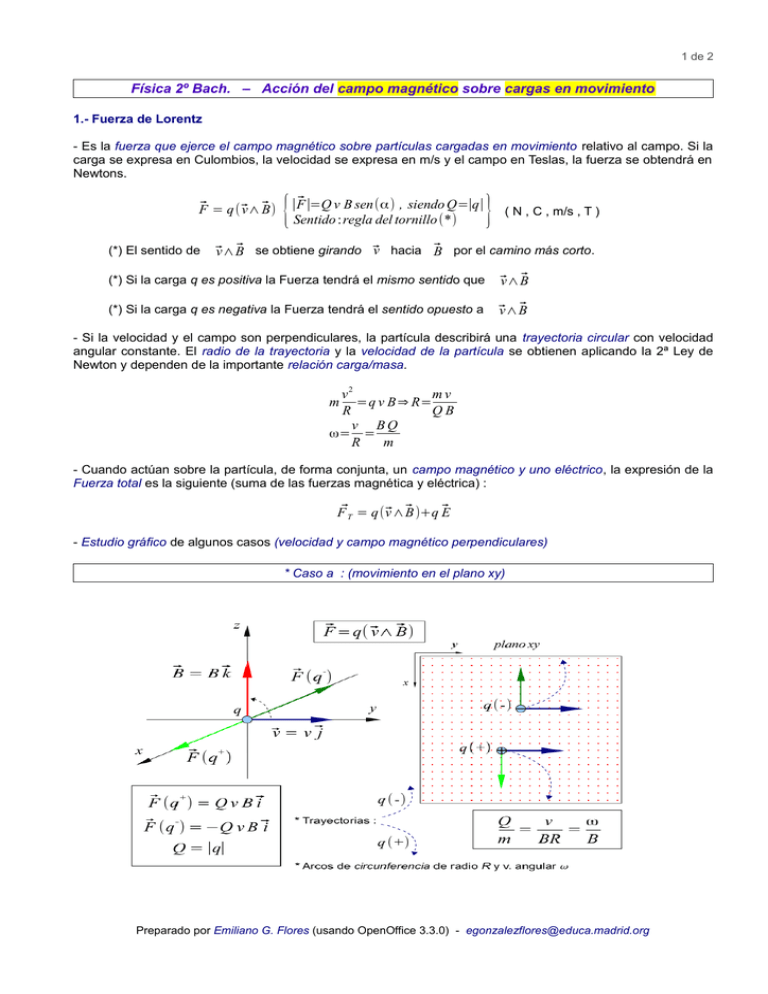
- Estudio gráfico de algunos casos (velocidad y campo magnético perpendiculares)
* Caso a : (movimiento en el plano xy)
Preparado por Emiliano G. Flores (usando OpenOffice 3.3.0) - [email protected]
2 de 2
* Caso b : (movimiento en el plano xz)
* Caso c : (movimiento en el plano yz)
Preparado por Emiliano G. Flores (usando OpenOffice 3.3.0) - [email protected]