TIPOS DE GRAFICOS Diagramas de puntos (Scatter Plot)

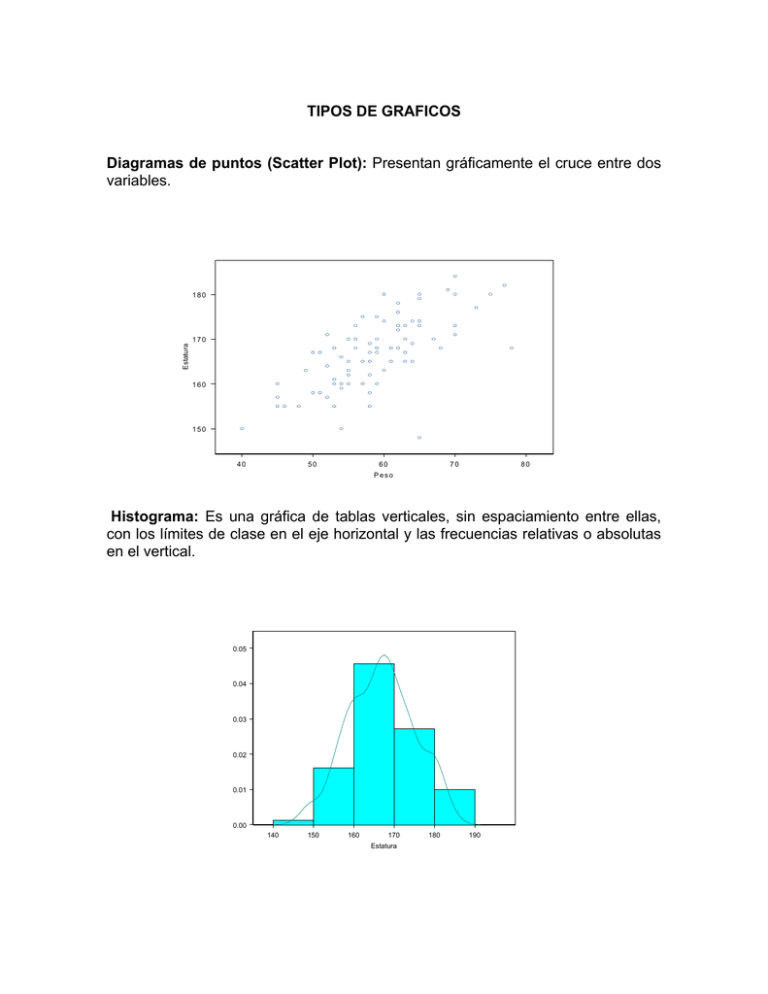
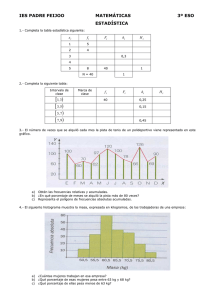
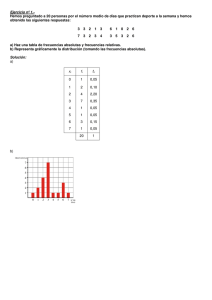
TIPOS DE GRAFICOS
Diagramas de puntos (Scatter Plot): Presentan gráficamente el cruce entre dos
variables.
180
Estatura
170
160
150
40
50
60
70
80
Peso
Histograma: Es una gráfica de tablas verticales, sin espaciamiento entre ellas,
con los límites de clase en el eje horizontal y las frecuencias relativas o absolutas
en el vertical.
0.05
0.04
0.03
0.02
0.01
0.00
140
150
160
170
Estatura
180
190
En el caso de las variables cualitativas y en algunas cuantitativas discretas, las
barras de la gráfica se encuentran espaciadas, en este caso el gráfico recibe el
nombre de diagrama de frecuencias.
80
60
40
20
0
0
1
2
3
4
5
6
7
8
Hermanos
Ojiva: Es un polígono de frecuencias acumuladas, donde el eje vertical presenta
las frecuencias acumuladas absolutas o relativas y el eje horizontal los límites
superiores de cada clase. La gráfica parte asignando frecuencia cero al límite
inferior de la primera clase.
Circular o de Torta (Pie): Es un círculo que está dividido en tantas regiones
como clases existan, y el área de dichas regiones es proporcional a la frecuencia
observada.
Tallo y Hoja (Stem-and-Leaf): Este diagrama muestra la distribución de
frecuencias, y una de las ventajas es que no perdemos información sobre los
datos en sí. El tallo está compuesto por la parte entera de las observaciones y las
hojas por la parte decimal.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
64
75
64
84
73
79
63
71
76
51
49
51
65
68
49
84
60
68
63
33
Tallo y Hoja
2
3
4
5
6
7
8
9
3
99
11
44358083
53916
44
Para los primeras
20 observaciones
de la columna A
de los pacientes
con cáncer
Cajón con Bigotes (Box Plot): Este es un diagrama de caja que muestra la
dispersión de los datos. El siguiente esquema muestra la forma de construirlo
BoxBox-plot
70
60
Mediana
1er Cuartil
40
3er Cuartil
50
80
Máximo
Mínimo
Promedio y Desviación : Muestra gráficamente el promedio de un conjunto de
datos y el error estándar. Este último mide la variabilidad esperada del promedio
muestral como estimación de la media poblacional, depende del tamaño de la
muestra y se calcula como:
SEM =
s
n
Media y Error Estándar
80
x + 2 × SEM
70
60
50
40
x
x − 2 × SEM