DERIVACION. Recta Tangente a una curva.

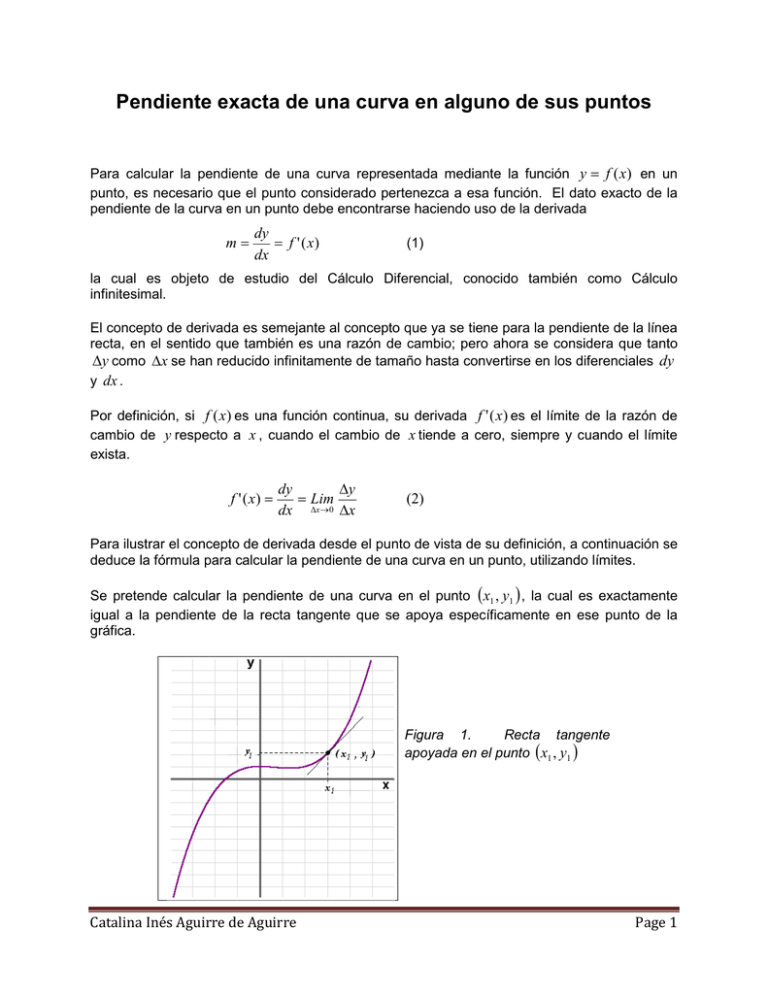
Pendiente exacta de una curva en alguno de sus puntos
Para calcular la pendiente de una curva representada mediante la función y = f (x) en un
punto, es necesario que el punto considerado pertenezca a esa función. El dato exacto de la
pendiente de la curva en un punto debe encontrarse haciendo uso de la derivada
m=
dy
= f ' ( x)
dx
(1)
la cual es objeto de estudio del Cálculo Diferencial, conocido también como Cálculo
infinitesimal.
El concepto de derivada es semejante al concepto que ya se tiene para la pendiente de la línea
recta, en el sentido que también es una razón de cambio; pero ahora se considera que tanto
∆y como ∆x se han reducido infinitamente de tamaño hasta convertirse en los diferenciales dy
y dx .
Por definición, si f (x) es una función continua, su derivada f ' ( x) es el límite de la razón de
cambio de y respecto a x , cuando el cambio de x tiende a cero, siempre y cuando el límite
exista.
f ' ( x) =
dy
∆y
= Lim
dx ∆x →0 ∆x
(2)
Para ilustrar el concepto de derivada desde el punto de vista de su definición, a continuación se
deduce la fórmula para calcular la pendiente de una curva en un punto, utilizando límites.
Se pretende calcular la pendiente de una curva en el punto ( x1 , y1 ) , la cual es exactamente
igual a la pendiente de la recta tangente que se apoya específicamente en ese punto de la
gráfica.
Figura 1.
Recta tangente
apoyada en el punto ( x1 , y1 )
Catalina Inés Aguirre de Aguirre
Page 1
Por otro lado sabemos que la pendiente de una línea recta se calcula haciendo uso de las
coordenadas de dos puntos que pertenezcan a la recta en cuestión
 y − y  ∆y
m =  2 1  =
 x 2 − x1  ∆x
en donde ( x1 , y1 ) y
considerada.
(x 2 , y 2 )
son puntos ubicados en el lugar geométrico de la línea recta
Si se toman dos puntos en una curva para calcular la pendiente de una recta secante,
realmente se está encontrando la pendiente aproximada de un segmento de la curva que nos
interesa.
Figura 2. Recta secante que pasa
por dos puntos de una curva.
Asimismo, se pueden tomar los dos puntos cada vez mas cerca uno de otro, a fin de que el
segmento considerado de la curva, sea cada vez más pequeño.
El procedimiento se inicia considerando que la pendiente de un segmento de una curva situado
entre dos puntos, es igual a la pendiente de la recta secante que pasa por esos puntos.
Se continúa, calculando la pendiente de rectas secantes que tocan puntos cada vez mas
cercanos entre sí.
El procedimiento finaliza cuando la distancia entre los dos puntos desaparece, quedando la
recta apoyada en un solo punto, por lo que la recta secante que se consideró al inicio, se ha
transformado en una recta tangente.
Los puntos a considerar son: ( x1 , y1 )
(x 2 , y 2 )
(3)
los cuales se muestran en la gráfica de la figura 2, en donde se ha utilizado la gráfica de la
función y = x 3 − x 2 + 1
Catalina Inés Aguirre de Aguirre
Page 2
La distancia en el eje x, entre las coordenadas horizontales de ambos puntos es ∆x .
Asimismo, ∆y es la distancia en el eje y entre las coordenadas verticales de los mismos
puntos.
 y 2 − y1  ∆y
 =
 x 2 − x1  ∆x
Al igual que en cualquier línea recta, la pendiente de la recta secante es: 
Figura 3(a). Vista ampliada de la
recta secante que pasa por dos
puntos de una curva.
A medida que la distancia entre los dos puntos se hace mas pequeña, se reducen las
dimensiones tanto de ∆x como de ∆y .
El proceso mediante el cual ∆y se transforma en dy , y ∆x en dx , equivale a decir que los
puntos considerados para trazar la secante, se acercan cada vez más hasta llegar a ser un solo
punto, por lo cual la recta considerada deja de ser secante para transformarse a tangente. Este
proceso es lo que está implícito cuando “se evalúa el límite cuando ∆x tiende a cero”.
f ' ( x) =
dy
∆y
= Lim
dx ∆x →0 ∆x
Cuando se dice que ∆x tiende a cero, se pretende que el punto ( x 2 , y 2 ) se acerque al punto
(x1 , y1 ) , buscándolo como meta.
Definitivamente, una función no puede derivarse en aquellos
puntos en los cuales es discontinua, por lo cual ( x1 , y1 ) debe pertenecer a la función.
La recta secante para el cálculo de la pendiente en ( x1 , y1 ) se planteó en la Figura 2 con un
∆x que debe reducirse a su mínima expresión. El resultado es la Figura 1 en donde se
muestra una recta tangente que se apoya en el punto ( x1 , y1 )
Para efectos de ilustrar de una forma numérica, el procedimiento descrito, a continuación se
toman específicamente los puntos que corresponden a x1 = 1.5 y x 2 = 2
Catalina Inés Aguirre de Aguirre
Page 3
(x1 , y1 ) = (1.5 , 2.125)
(x2 , y 2 ) = (2 , 5)
Figura 3(b) Datos numéricos
correspondientes a la gráfica
3(a)
La pendiente de la recta secante que pasa por estos dos puntos de la curva es:
 y 2 − y1  ∆y 5 − 2.125 2.875

 =
=
=
= 5.75
2 − 1.5
0.5
 x 2 − x1  ∆x
En las Figuras 3(b), 4 y 5, se muestra varios acercamientos de la misma gráfica de la Figura 2,
en la que se observa que cuando ∆x se hace más pequeño, automáticamente ∆y también se
hace más pequeño.
Para hacer el acercamiento que se presenta en la Figura 3(b), se eligió una ventana cuyas
dimensiones son:
0≤ x≤3
0 ≤ y ≤ 10
Para trazar la Figura 4, se amplió una porción de la Figura 3(b).
dimensiones
1≤ x ≤ 2
0≤ y≤4
Los puntos considerados corresponden a x1 = 1.5 y
Esta ventana tiene las
x 2 = 1.6
La pendiente de la recta secante que pasa por estos dos puntos de la curva es:
 y 2 − y1  ∆y 2.536 − 2.125 0.411

 =
=
=
= 4.11
1.6 − 1.5
0.1
 x 2 − x1  ∆x
Catalina Inés Aguirre de Aguirre
Page 4
Figura 4. Recta secante que pasa por los puntos:
(x1 , y1 ) = (1.5 , 2.125)
(x2 , y 2 ) = (1.6, 2.536)
Finalmente se tomó una ventana con dimensiones 1.45 ≤ x ≤ 1.55
la Figura 5,
1.9 ≤ y ≤ 2.4 para trazar
Figura 5. Recta secante que pasa por los
puntos:
(x1 , y1 ) = (1.5 , 2.125)
(x 2 , y 2 ) = (1.51, 2.162851)
La pendiente de la recta secante que pasa por estos dos puntos de la curva es:
 y 2 − y1  ∆y 2.162851 − 2.125 0.037851

 =
=
=
= 3.7851
1.51 − 1.5
0.01
 x 2 − x1  ∆x
Como puede verse, a medida que ∆x se hace más pequeño, la recta secante se apoya en dos
puntos cada vez más cercanos. Cuando ∆x ha disminuido suficiente para que su valor casi
sea cero, la recta secante prácticamente se está apoyando solamente en el punto ( x1 , y1 ) , por
lo que se considera que es la recta tangente mostrada en la Figura 1.
Otro aspecto a favor de que se considere una línea recta como referencia para calcular la
pendiente de una curva en un punto, es que a medida que se amplifica la ventana alrededor del
punto ( x1 , y1 ) , la curvatura de la gráfica se hace menos perceptible hasta llegar a ser una línea
recta cuando estamos llegando a valores sumamente pequeños de ∆x y de ∆y .
Catalina Inés Aguirre de Aguirre
Page 5
El concepto de “diferencial” se ubica precisamente en la situación en que ∆x se ha reducido
tanto, que su valor es casi cero. Por tanto, todo lo que se ha mencionado respecto a la
pendiente de la recta secante calculada con límites, es conceptualmente válido al referirse a
diferenciales.
De acuerdo a la definición de derivada, la fórmula para el cálculo de la pendiente de una recta
tangente que se apoya en cualquier punto de una función, ya mencionada como ecuación (2),
es:
m = f ' ( x) =
dy
∆y
= Lim
∆
x
→
0
dx
∆x
(x1 , y1 ) y (x 2 , y 2 ) les llamamos respectivamente punto (x, f ( x))
f ( x + ∆x) ) y se sustituyen en la ecuación anterior, la ecuación toma la forma
Si a los puntos
(x + ∆x,
f ' ( x) =
dy
f ( x + ∆x ) − f ( x )
= Lim
dx ∆x →0 ( x + ∆x) − x
y punto
(4)
finalmente, simplificando los términos semejantes, se llega a:
f ' ( x) =
dy
f ( x + ∆x ) − f ( x )
= Lim
∆
x
→
0
dx
∆x
(5)
la cual implica el cálculo de la pendiente de una recta secante en el límite cuando ∆x tiende a
cero.
Algunos autores utilizan h en lugar ∆x , lo cual solo es un cambio de simbología y no altera
en lo absoluto el tema tratado.
__________________________________________________________________________
Ejercicio resuelto
Usando la definición de derivada (en términos de límites),
a) Encuentre la ecuación para el cálculo de la pendiente en cualquier punto para la función
y = f ( x) = x 3 − x 2 + 1 , la cual corresponde a la gráfica de la Figura 1.
b) Calcule la pendiente exacta de la misma función en x =1.5
Resolviendo
a) Para empezar, debe establecerse f ( x + ∆x) para la función planteada. Esto es:
f ( x + ∆x) = (x + ∆x ) − ( x + ∆x ) + 1
3
Catalina Inés Aguirre de Aguirre
2
Page 6
Utilizando la ecuación (5)
f ' ( x) =
dy
f ( x + ∆x ) − f ( x )
= Lim
dx ∆x →0
∆x
sustituyendo los polinomios que corresponden a f (x) y a f ( x + ∆x)
(x + ∆x ) − ( x + ∆x) 2 + 1 − ( x 3 − x 2 + 1)
dy
= Lim
dx ∆x →0
∆x
3
f ' ( x) =
desarrollando los binomios elevados a una potencia,
f ' ( x) =
(
dy
x 3 + 3 x 2 ∆x + 3 x ( ∆x ) 2 + ( ∆x ) 3
= Lim
dx ∆x →0
)
− ( x 2 + 2 x∆x + (∆x) 2 ) + 1 − ( x 3 − x 2 + 1)
∆x
simplificando los términos semejantes y sacando un factor común, se tiene
(
∆x 3 x 2 + 3 x∆x + (∆x) 2 − 2 x + ∆x
dy
= Lim
f ' ( x) =
dx ∆x →0
∆x
)
simplificando ∆x en numerador y denominador
f ' ( x) =
dy
= Lim (3 x 2 + 3 x∆x + (∆x) 2 − 2 x + ∆x)
dx ∆x →0
evaluando el límite cuando ∆x → 0
m=
dy
= f ' ( x) = 3x 2 − 2 x
dx
Esta respuesta proporciona una fórmula para calcular la pendiente de y = f ( x) = x 3 − x 2 + 1
en cualquier punto.
b) Para x = 1.5 el valor de la pendiente se obtiene evaluando la derivada en x = 1.5
f ' ( x) = 3x 2 − 2 x
f ' (1.5) = 3(1.5) − 2(1.5) = 3.75
2
El valor 3.75 obtenido para la derivada, es el valor de la pendiente de la recta tangente que se
apoya en el punto de la curva en donde x=1.5
__________________________________________________________________________
Catalina Inés Aguirre de Aguirre
Page 7