Ejercicio 1 (26 puntos ) i) Halle una función cuadrática P(x) cuya gráfi

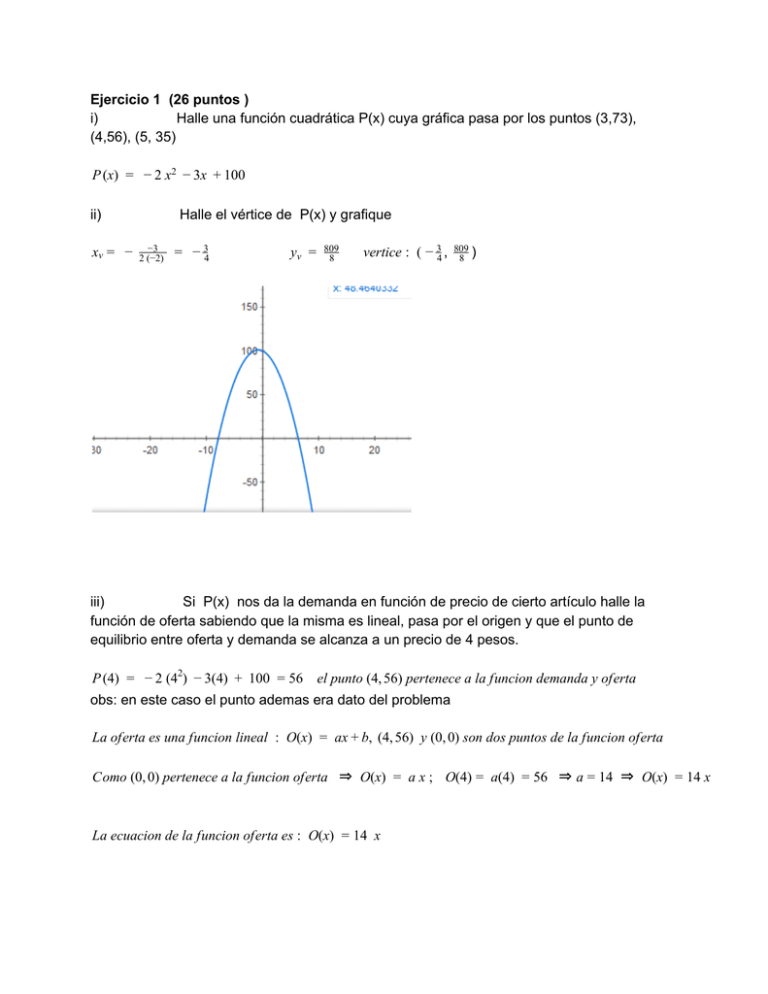
Ejercicio 1 (26 puntos ) i) Halle una función cuadrática P(x) cuya gráfica pasa por los puntos (3,73), (4,56), (5, 35) P (x) = − 2 x2 − 3x + 100 ii) Halle el vértice de P(x) y grafique −3 = − 3 y = 809 vertice : ( − 3 , 809 ) xv = − 2 (−2) v
4
8
4
8
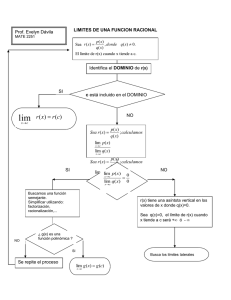
iii) Si P(x) nos da la demanda en función de precio de cierto artículo halle la función de oferta sabiendo que la misma es lineal, pasa por el origen y que el punto de equilibrio entre oferta y demanda se alcanza a un precio de 4 pesos. P (4) = − 2 (42) − 3(4) + 100 = 56 el punto (4, 56) pertenece a la funcion demanda y oferta obs: en este caso el punto ademas era dato del problema La oferta es una funcion lineal : O(x) = ax + b, (4, 56) y (0, 0) son dos puntos de la funcion oferta C omo (0, 0) pertenece a la funcion oferta ⇒ O(x) = a x ; O(4) = a(4) = 56 ⇒ a = 14 ⇒ O(x) = 14 x
La ecuacion de la funcion oferta es : O(x) = 14 x iv) Grafique oferta y demanda indicando el punto de equilibrio Ejercicio 2 (30 puntos) Sea f : R → R i) Grafique f ii) Analice si f es inyectiva y/o sobreyectiva. Justifique el resultado f (0) = f(2) =− 1 por lo que f no es inyectiva C od (f) = R = Rec (f) por lo que f es sobreyectiva iii) ¿Es f invertible? Justifique y de ser necesario restrinja el dominio y/o el codominio (manteniéndolos lo más grande posible) para que lo sea. Al no ser f inyectiva, f no es biyectiva y por lo tanto no es invertible. f es sobreyectiva y no es inyectiva por lo que hay que reducir dominio para que sea inyectiva. Algunos de los posibles dominios (hay infinitas posibles soluciones) A = { x ∈ R/ x < − 1} ⋃{ x ∈ R/ x ≥ 1} B = { x ∈ R/ x < 0} ⋃{ x ∈ R/ x ≥ 2} iv) Halle la función inversa de f con el dominio y codominio de iii) f : A → R f −1(y) = − √y + 1 si y > 0 f −1(y) = 1 + √ − y si y ≤ 0 f : B → R f −1(y) = − √y + 1 si y > − 1 f −1(y) = 1 + √ − y si y ≤− 1 v) f −1 : R → A Ejercicio 3 ( 24 puntos) Calcule los siguientes límites justificando los resultados: i) ii) pues ln u ~ u­1 cuando u tiende a 1 y tiende a 1 cuando x tiende a + infinito porque en + infinito los polinomios son equivalentes al termino de mayor grado iii) numerador y denominador tienden a +infinito pero, como iv) , el limite es 0 ​
pues Ejercicio 4 ( 20 puntos) Investigue si las siguientes funciones son continuas en el punto que se indica: −x2 +1
i) lim − f (x) = lim − e x+1 −1 usando el equivalente eu − 1 ~ u si u tiende a 0 x→ −1
lim −
x→ −1 x→ −1 −x2+1 x +1 = lim −
x→ −1 (−x+1) (x+1)
x +1 = lim − − x + 1 = 2 x→ −1 x+1
lim + f(x) = lim + (x + 3) e x→ −1
x→ −1 = 2 entonces lim f (x) = lim − f (x) = lim + f(x) = 2 x→ −1
x→ −1
x→ −1
f (− 1) = (− 1 + 3) e −1+1 = 2 lim f (x) = 2 = f (− 1) x→ −1
f es continua en x=­1 ii) 2
lim− f(x) = lim− 4x −12 x + 8 = lim−
x2−4
x→ 2
x→ 2 x→ 2 4 (x −2) (x−1)
(x − 2) (x + 2) = lim−
x→ 2 4 (x − 1)
x +2 = 1 lim f(x) = lim+ 2 + L (x − 1) = 2 o f(2) = 2 + L(2 − 1) = 2 x→ 2+
x→ 2 lim f (x) =/ lim+ f(x) entonces no existe lim f (x) x→ 2−
x→ 2
f no es continua en x=2 x→ 2