Solución Caso Técnico

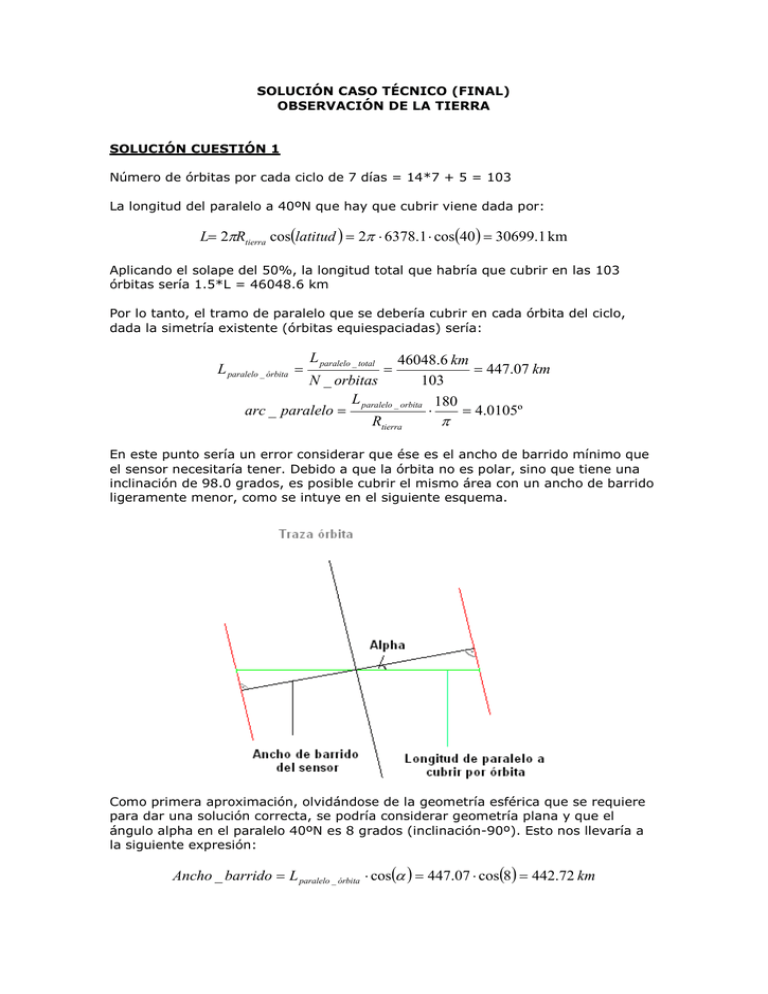
SOLUCIÓN CASO TÉCNICO (FINAL)
OBSERVACIÓN DE LA TIERRA
SOLUCIÓN CUESTIÓN 1
Número de órbitas por cada ciclo de 7 días = 14*7 + 5 = 103
La longitud del paralelo a 40ºN que hay que cubrir viene dada por:
L= 2πRtierra cos(latitud ) = 2π ⋅ 6378.1 ⋅ cos(40 ) = 30699.1 km
Aplicando el solape del 50%, la longitud total que habría que cubrir en las 103
órbitas sería 1.5*L = 46048.6 km
Por lo tanto, el tramo de paralelo que se debería cubrir en cada órbita del ciclo,
dada la simetría existente (órbitas equiespaciadas) sería:
L paralelo _ órbita =
L paralelo _ total
=
46048.6 km
= 447.07 km
103
N _ orbitas
L paralelo _ orbita 180
arc _ paralelo =
⋅
= 4.0105º
Rtierra
π
En este punto sería un error considerar que ése es el ancho de barrido mínimo que
el sensor necesitaría tener. Debido a que la órbita no es polar, sino que tiene una
inclinación de 98.0 grados, es posible cubrir el mismo área con un ancho de barrido
ligeramente menor, como se intuye en el siguiente esquema.
Como primera aproximación, olvidándose de la geometría esférica que se requiere
para dar una solución correcta, se podría considerar geometría plana y que el
ángulo alpha en el paralelo 40ºN es 8 grados (inclinación-90º). Esto nos llevaría a
la siguiente expresión:
Ancho _ barrido = L paralelo _ órbita ⋅ cos(α ) = 447.07 ⋅ cos(8) = 442.72 km
arc _ swath =
ancho _ barrido 180
⋅
= 3.977º
RTierra
π
Pero realmente, el problema a solucionar es de geometría esférica, como se indica
en la siguiente figura.
Hay que resolver dos triángulos esféricos rectángulos. El triángulo 2 no sería
realmente esférico, ya que el arco del paralelo que se ha de cubrir con el ancho de
barrido no pertenece a un círculo máximo de la esfera. Pero se podría considerar
que es prácticamente idéntico al arco del círculo máximo que pasa por los dos
extremos del arco.
De TR1 se obtiene:
cos(180 − inclinación) = cos(latitud ) ⋅ sen(C )
 cos(180 − inclinación ) 
 cos(82 ) 
 = arcsen
 = 10.467 º
C = arcsen
cos(latitud )


 cos(40 ) 
Y con este resultado ya se puede abordar el segundo triángulo esférico (TR2):
tan (arc _ swath ) = tan (arc _ paralelo ) ⋅ cos(C )
arc _ swath = arctan(tan (arc _ paralelo ) ⋅ cos(C )) = arctan(tan (4.0105) ⋅ cos(10.467 )) = 3.9440º
Ancho _ barrido = arc _ swath ⋅ RTierra ⋅
π
180
= 439.04 km
Ahora ya se está en condiciones de dar el último paso, que es calcular el FOV,
resolviendo el triángulo de la figura.
 arc _ swath 
 FOV 
sen
⋅
 = sen
2


 2 
R
 arc _ swath 
2
R 2 + (R + h ) − 2 R(R + h ) cos

2


Aplicando esta fórmula:
FOV = 37.077º, si se ha realizado el cálculo correctamente con triángulos esféricos
FOV = 37.363º, si se ha tomado la simplificación de considerar geometría plana
SOLUCIÓN CUESTIÓN 2
Con el resultado de la cuestión anterior y el resto de datos del problema se tiene
que el instrumento observa, en cada ciclo de repetición de la órbita de 7 días, 2
veces la mitad del territorio español y una vez la otra mitad. Se pueden usar los
datos estadísticos de la tabla para estimar la probabilidad de que una observación
sobre España en noviembre tenga una cobertura de nubes menor del 15%. Sería:
P<15% =
(Observaciones < 15% ) = (18 + 25 + 36) = 0.2633
Observaciones _ totales
300
Si asumimos que cada pasada es independiente de las demás, la probabilidad de
que al menos una pasada tenga una cobertura de nubes menor del 15%, cuando
se consideran n pasadas es:
P1 pasada = 1 − P0 pasadas = 1 − (1 − P<15% )
n
Dado el ciclo orbital de 7 días, en un mes se tendrán 4 pasadas en un 50% del área
y 8 pasadas en el otro 50%. Aplicando la fórmula anterior para n=4 y n=8:
P1 pasada = 1 − (1 − 0.2633) = 0.705 , o sea, 70.5% de probabilidades de tener al menos
4
una cobertura completa en un 50% del área.
P1 pasada = 1 − (1 − 0.2633) = 0.913 , o sea, 91.3% de probabilidades de tener al menos
8
una cobertura completa en el restante 50% del área.
En resumen, las zonas de España donde se tiene un solape del ancho de barrido, se
puede asegurar la cobertura mensual con una probabilidad del 91.3%, superior al
90% pedido en el requisito. En el 50% restante del área del territorio español, la
probabilidad de tener una cobertura global en un mes sería inferior a la requerida
(70.5%), no cumpliéndose el requisito.
Para reformular el requisito, habría que asegurarse de que en las zonas de 4
observaciones mensuales el requisito también se cumpliera, para lo cual habría que
aumentar el límite máximo de nubes requerido, hasta un valor que hiciera que:
P1 pasada = 1 − (1 − P ) = 0.9
4
P = 1 − 4 1 − 0.9 = 0.4377
Lo que se consigue haciendo que el porcentaje de nubes sea menor que el 25%:
P< 25% =
(Observaciones < 25%) = (18 + 25 + 36 + 29 + 24) = 0.44
Observaciones _ totales
300
El requisito reformulado sería:”la misión debe proporcionar una cobertura total
libre de nubes del territorio español al mes (límite del 25% de cobertura de
nubes, probabilidad>90%)”.
SOLUCIÓN CUESTIÓN 3
El sun glint es producido por la reflexión especular de la luz del sol incidiendo en el
instrumento. Sabiendo que la hora local del nodo ascendente son las 10:30, el
ángulo que forma la línea de nodos con la dirección del sol medio (alpha, en la
figura 2 del enunciado) sería de 22.5 grados:
α=
HLNA − 12 : 00
⋅ 360º = 22.5º
24
Si hacemos la aproximación de que este ángulo es el menor Sun Zenith Angle en la
órbita y que se daría en las proximidades del ecuador (en realidad el mínimo es
22.27º en 3.4ºS, tomando sol medio), habría que comprobar si la reflexión
especular de los rayos de sol incide en el instrumento en algún punto del swath.
Tomando como base la siguiente figura, se puede apreciar que la zona situada en el
extremo derecho del swath sería la única con opciones de sufrir sun glint.
El ángulo de incidencia en tierra del extremo derecho del swath es de 20.51 grados.
(
)
 (R + h ) ⋅ sin FOV 
2  = 20.51º
ángulo _ incidencia = arcsin

R



Este ángulo es muy cercano a los 22.5 grados de incidencia del sol, con lo que este
análisis sencillo nos indica que, si bien la reflexión puramente especular no llegaría
a incidir en el instrumento, habría que estudiar en más detalle lo que ocurre en el
extremo derecho del swath. En la realidad, la reflexión sobre el agua depende de
ciertos factores, como la velocidad del viento en superficie (formación de olas), que
hacen que la reflexión no sea puramente especular. Dada la cercanía de los 2
ángulos de incidencia, se puede esperar que altos niveles de radiancia procedentes
de reflexiones casi-especulares afecten al extremo derecho del swath. Si por un
momento no consideramos sol medio, sino el sol real, los puntos y épocas a
analizar serían las cercanías del ecuador durante los equinoccios y las cercanías del
trópico correspondiente durante los solsticios.
Con respecto a la radiancia de sun glint, para un ancho de banda cualquiera
tendríamos:
Radiancia = coeff _ reflex ⋅
Irradiancia _ solar
Ángulo _ sólido ⋅ Ancho _ banda
Para componer la banda deseada (de 450 a 520 nm), hay que usar los valores de
irradiancia de la tabla, excepto el primero y el último. Sumando esos valores
tendríamos la irradiancia solar total en la banda de 70 nm.
Irradiancia _ banda 70nm = ∑ Irradiancias (455nm − 515nm ) ⋅ 10 4
cm 2
W
W
⋅ 10 −6
= 136.01 2
2
µW
m
m
Con respecto al ángulo sólido, se sabe que el ángulo sólido sostenido por un cono
de apertura γ es:
Ángulo _ sólido _ cono = 2π ⋅ (1 − cos γ )
La reflexión puramente especular de la luz solar se realizaría sobre el ángulo sólido
correspondiente a un cono de apertura 16 minutos de arco:
Ángulo _ sólido = 2π ⋅ (1 − cos(0.26667 º )) = 6.805 ⋅ 10 −5 sr
Con lo que ya se estaría en condiciones de obtener la radiancia debida al sun glint
en esa banda del instrumento:
Radiancia _ sun _ gl int = 0.04 ⋅
136.01W
W
m2
= 1.142 ⋅ 10 6 2
−5
6.805 ⋅ 10 sr ⋅ 0.07 µm
m ⋅ sr ⋅ µm