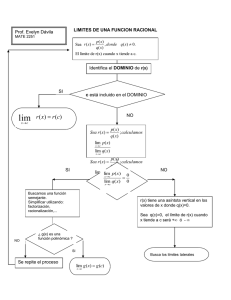
Límite de una función

9
1
Límite de una función
SOLUCIONARIO
Límite de una función
LITERATURA Y MATEMÁTICAS
El ocho
Sharrif iba sacando los libros [de mi bolsa] y ordenándolos en una
pila sobre el escritorio mientras leía cuidadosamente los títulos.
–Juegos matemáticos de ajedrez... ¡ah! ¡Los números de Fibonacci! –exclamó, con esa sonrisa que me hacía sentir que tenía algo contra mí.
Señalaba el aburrido libro de Nim–. ¿De modo que te interesan las
matemáticas? –preguntó, mirándome con intención.
–No mucho –dije, poniéndome en pie y tratando de volver a guardar
mis pertenencias en la bolsa. [...]
–¿Qué sabe exactamente sobre los números de Fibonacci? [...]
–Se usan para proyecciones de mercado –murmuré–. [...]
–¿Entonces no conoce al autor? [...] Me refiero a Leonardo Fibonacci.
Un italiano nacido en Pisa en el siglo XII, pero educado aquí, en Argel.
Era un brillante conocedor de las matemáticas de aquel moro famoso,
Al-Kwarizmi, que ha dado su nombre a la palabra «algoritmo». Fibonacci introdujo en Europa la numeración arábiga, que reemplazó a los
viejos números romanos...
Maldición. Debí haber comprendido que Nim no iba a darme un libro sólo para que me entretuviera, aun cuando lo hubiera escrito él mismo. [...]
Permanecí leyéndolo casi hasta el amanecer y mi decisión había resultado productiva, aunque no sabía con certeza cómo. Al parecer, los números de Fibonacci se usan para algo más que las proyecciones del mercado
de valores. La resolución de un problema había llevado a Fibonacci a formar esta interesante sucesión de números empezando por el uno y sumando a cada número al precedente: 1, 1, 2, 3, 5, 8, 13, 21... [...] Descubrió que los cocientes entre cada término y el anterior se aproximan al
número 1 + 5 y que este número describía también la estructura
2
de todas las cosas naturales que formaban una espiral.
KATHERINE NEVILLE
Los números de Fibonacci aparecen con frecuencia en la naturaleza. Por ejemplo, el número
de espirales de los girasoles o de las piñas es siempre uno de estos números.
Además, como se dice en esta novela, al dividir cada término de la sucesión de Fibonacci
entre el anterior, se obtiene una nueva sucesión de números que se aproximan
1+ 5
cada vez más al número de oro:
. Aunque no la descubrió Fibonacci, esta propiedad
2
es verdadera. Compruébala tú mismo.
La sucesión que se obtiene al dividir cada término de la sucesión de Fibonacci entre el anterior es:
a1 = 1
a3 =
a2 = 2
a4 =
3
2
5
3
Estos valores se aproximan a:
380
= 1, 5
a5 =
= 1,6º
a6 =
1+ 5
= 1, 618…
2
8
5
13
8
= 1, 6
= 1, 625
a7 =
a8 =
21
13
34
21
= 1, 615…
= 1, 619…
SOLUCIONARIO
9
ANTES DE COMENZAR… RECUERDA
001
Escribe los términos 14, 123 y 2.345 de estas sucesiones.
n+4
a) an = n2 − 3 n + 2
b) an =
2n +1
a) a14 = 156
b) a14 =
002
18
29
a123 = 14.762
a123 =
a2.345 = 5.491.992
127
247
a2.345 =
2.349
4.691
Factoriza este polinomio: P(x) = 7x 5 + 14x 4 −35x 3 − 42x 2
P(x) = 7x2 (x − 2)(x + 1)(x + 3)
003
Simplifica estas fracciones algebraicas.
a)
x 2 + 2x + 1
x ( x + 1)
2
b)
x( x − 2)
2
( x − 9 )( y 2 − 16 )
2
x ( x − 4)
d)
x( x − 2)
xy ( 2x − 6 )( y + 4 )2
a)
x 2 + 2x + 1
x +1
( x + 1)2
=
=
x ( x + 1)
x ( x + 1)
x
b)
x2 ( x2 − 4 )
x 2 ( x + 2 )( x − 2 )
=
= x( x + 2)
x( x − 2)
x( x − 2)
c)
d)
004
y 2 ( x 2 − 4x + 4 )
c)
y2 ( x2 − 4 x + 4 )
x( x − 2)
=
( x 2 − 9 )( y 2 − 16 )
2
xy ( 2 x − 6 )( y + 4 )
y 2 ( x − 2 )2
x( x − 2)
=
=
y2 ( x − 2)
x
( x + 3 )( x − 3 )( y + 4 )( y − 4 )
2
2 xy ( x − 3 )( y + 4 )
=
( x + 3 )( y − 4 )
2 xy ( y + 4 )
Resuelve estas operaciones y simplifica el resultado.
a) ( x + 1) −
x 2 − 3x + 1
x −1
b) ( 2x − 2 ) −
x −1
3x
x 2 − 3x + 1
x 2 − 1− x 2 + 3 x − 1
3x − 2
=
=
x −1
x −1
x −1
2
2
x −1
6x − 6x − x + 1
6 x − 7x + 1
b) ( 2 x − 2 ) −
=
=
3x
3x
3x
a) ( x + 1) −
ACTIVIDADES
001
Obtén el término general de estas sucesiones.
a)
3 7 11
,
,
, …
5 15 45
a) an =
4n − 1
5 ⋅ 3n−1
b)
3 1 −1 −3
,…
, ,
,
1 4 9 16
b) an =
−2 n + 5
n2
381
Límite de una función
002
Con tu calculadora, halla los cinco primeros términos de la sucesión recurrente
a +3
an = n−1
, siendo a1 = 1, y determina el número al que se aproxima.
an−1 + 1
a1 = 1
a2 = 2
a3 =
5
= 1,6º
3
a4 =
b) an = n2
a) lim an = 1
n→ `
n →`
b) an = 4 − n
n→ `
n→ `
c) an = n2 + 3
d) an = ( −1)n+1
Calcula estos límites de sucesiones.
lim n3
a) n→
lim n
b) n→`
`
a) lim n3 = + `
n →`
lim 3 n 4
c) n→`
b) lim n = + `
n →`
0 , 5n
d) nlim
→`
c) lim 3 n4 = + `
n →`
d) lim 0 , 5n = 0
n →`
Halla los límites de las sucesiones cuyos términos generales son los siguientes.
8n
( n − 1)10
a)
b)
2 n2 + 3 n − 1
( n + 2 )10
a) lim
n →`
8n
=0
2
2 n + 3n − 1
( n − 1)10
=1
n →` ( n + 2 )10
b) lim
Halla los siguientes límites.
 3 n 2 −1
4 n 4 
a) lim 

⋅
n→` 
 n3
2 n 4 + 3 
b) lim ln
n→`
n2 + 7
2n
 3 n2 − 1
4 n4 
a) lim 
 = 0
⋅
n →` 
 n3
2 n4 + 3 
b) lim ln
382
d) lim an = 0
n →`
Escribe sucesiones de números reales que cumplan que su límite, cuando n
tiende a infinito, es:
a) lim an = 3
b) lim an = −`
c) lim an = + `
d) lim an no existe
Respuesta abierta.
3n
a) an =
n+1
007
d) an = 0 , 2 n
c) lim an = − `
n →`
n→ `
006
c) an = n2 − n3
b) lim an = + `
n →`
005
19
»
= 1,72
11
Con ayuda de tu calculadora, halla el límite de las siguientes sucesiones.
a) an = ( −1)2n+ 4
004
a5 =
3 = 1, 732…
Los términos de la sucesión se aproximan a:
003
7
= 1, 75
4
n2 + 7
= +`
2n
c) lim
n→`
3 n2 + 1
n2 + n + 2
 n+1
n −1 

−
d) lim 
n→`  n −1
n + 1 
c) lim
n →`
3 n2 + 1
=
n2 + n + 2
3
 n + 1 n − 1 

= 0
−
d) nlim
→` 
 n − 1 n + 1 
SOLUCIONARIO
008
Calcula estos límites.
 n4 + 1

−n3

lim  4
+
a) n→`
3
 2 n + 1
3 n + n + 1 
lim ln
b) n→`
n2 + 1
c) lim 9
2
d) lim 0 ,1 n
n →`
n2 +1
 n4 + 1

− n3
1
a) lim 
 =
+
4
3

n →`  2 n + 1
3 n + n + 1  6
n→`
009
2n2
n →`
n +1
2 n3 + 1
2 n3 + n
b) lim ln
9
c) lim 9
2n2
n→`
=3
n+1
2 n3 + 1
=0
2 n3 + n
d) lim 0 ,1 n2 = 1
n →`
Explica por qué no son indeterminaciones.
0
`
a) ` ⋅ `
b)
c)
0
`
d) `1
a) El producto de valores muy grandes resulta un valor aún más grande.
b) Al dividir cero entre cualquier número distinto de él, el resultado es cero.
c) El cociente de un valor muy grande entre un número muy próximo a cero
es un valor aún más grande.
d) Cualquier número elevado a uno es el mismo número.
010
Pon ejemplos de límites que produzcan indeterminaciones de los tipos.
b) 1`
a) 0 ⋅ `
c) `0
d) 00
Respuesta abierta.
n
1
 1
a) lim   ln n
n →` 
 4 
c) lim ( n − 4 ) n
n →`
2n
 1
d) lim  2
n →`  n
 n + 1 
b) lim 

n →` 
 n − 1 
011
1
 n


Calcula los siguientes límites, resolviendo las indeterminaciones que puedan presentar.
a) lim
n→`
n +3n
n
a) lim
n→ `
lim
n →`
b) lim
n→ `
lim
n →`
b) lim
n→`
n+ n+1
2n
n +3n
`
→
n
`
n +3n
=0
n
n+ n+1
`
→
2n
`
1
n+ n+1
=
2n
2
383
Límite de una función
012
¿Presentan indeterminaciones del tipo
`
estas sucesiones?
`
En caso afirmativo, halla el límite.
3
5 − n2
n
a) lim
n→`
b) lim
n→`
5 − n2
n
a) No es una indeterminación, porque la raíz cuadrada no está definida
para valores grandes de n.
3
5 − n2
`
b) Es una indeterminación del tipo : lim
=0
` n→`
n
013
Calcula los siguientes límites.
 n4
−n3 + 2 
b) lim 

+

n→` 
 n2 + 1
n
 n3 + 2 n + 1
n2 
a) lim 

−
n→` 
 2 n 2 −1
n −1 
 n3 + 2 n + 1
n2 
 → ` − `
−
a) lim 
n→ ` 
2 n2 − 1
n − 1 
 n3 + 2 n + 1
− n4 − n3 + 3 n2 − n − 1
n2 
 = lim
= −`
lim 
−
n→ ` 
n − 1  n→ ` 2 n3 − 2 n2 − n + 1
2 n2 − 1
 n4
− n3 + 2 
 → ` − `
+
b) lim  2

n→ ` 
 n +1
n
 n4
− n3 + 2 n2 + 2
− n3 + 2 
 = lim
+
= −1
lim  2
 n→ `
n→ `  n + 1
n3 + n
n
014
Halla estos límites.
a) lim
n→`
( n2 − 4 − n2 − 3 n )
b) lim (2 n − n2 + 5 )
n→`
c) lim
n→`
(
n2 + 7 + 3 n2 + n )
a) lim ( n2 − 4 − n2 − 3 n ) → ` − `
n→ `
lim ( n2 − 4 − n2 − 3 n ) = lim
n→ `
n→ `
3n − 4
2
2
n − 4 + n − 3n
b) lim (2 n − n2 + 5 ) → ` − `
n→ `
lim (2 n − n2 + 5 ) = lim
n→ `
n→ `
3 n2 − 5
2
4n + n + 5
c) lim ( n2 + 7 + 3 n2 + n ) = + `
n →`
384
2
=
3
4
=
3
2
9
SOLUCIONARIO
015
Calcula los siguientes límites.
n
2n


1 + 1  5
a) nlim


→` 
n 


1− 1  3
b) nlim


→` 
n 
n
2n
2n
−n


13
1  
 
lim 1−  = lim 1 +
n→ ` 
n→ ` 

n 
− n  


13
b) lim 1−  → 1`
n→ ` 

n 
016
1
n
n
1


1 5
1  5
lim 1 +  = lim 1 +   = e 5

n→ ` 
n → ` 
n 
n  


1 5
a) lim 1 +  → 1`

n→ ` 
n 
−
2
3
=e
−
2
3
Halla estos límites.
3n−2
n

5
a) lim 1 + 
n →` 
n 

3 

b) lim 1 +
n →` 
2 n 
5
n 



 5 

5
1
  = e 5
lim 1 +  = lim 1 +
n→ ` 
n → ` 
 

n
n 


 

5  
n
n

5
a) lim 1 +  → 1`
n→ ` 

n 
3n−2
3 n−2

3 
b) lim 1 +

n→ ` 

2 n 
017

3 

lim 1 +
n→ ` 

2 n 
→ 1`
3 ( 3n−2 )
2n
9
= e2
Halla los siguientes límites.
3
 2 x 

a) lim 
x →+ `  x −1 

b)
3
a)
018
2n 


 3 
1
 
= lim 1 +
n→ ` 
 
2
n


 

3  
 2 x 
 = 23 = 8
lim 
x →+ ` 
 x − 1 
Calcula estos límites.
x
 x + 1 



a) x lim
→+ ` 
 3x + 3 
lim
x →+ `
( 3 x + 1) x 4
( x 2 − 6 )( 2 x −1)3
( 3 x + 1) x 4
3
=
2
3
x → +` ( x − 6 )( 2 x − 1)
8
b) lim
 x 2 + 2 x 

b) lim  2
x →+ `  x + 1 

x
x
a)
 x + 1 
 =0
lim 
x → +` 
 3 x + 3 
x
 x 2 + 2 x 
 → 1`
b) lim  2
x → +` 
 x + 1 

lim 
x → +` 
x 2 +1 

x
x
2






1  2x −1 
x + 2x 
2 x − 1
1 +
 = lim 1 +


=
lim

2

x → +` 
x → +` 


1
x 2 + 1 
x
x 2 + 1 
+







2 x − 1 


x ( 2 x −1 )
x 2 +1
= e2
385
Límite de una función
019
Calcula los límites laterales en el punto x = 3 de:
 x − 3 si x < 3
f (x) =  2
 x + 1 si x ≥ 3
lim f ( x ) = lim+ ( x 2 + 1) = 10
lim f ( x ) = lim− ( x − 3) = 0
x → 3−
020
x →3
x −1
x2
b) f ( x ) =
a) lim− f ( x ) = − `
1
b) f ( x ) = 
−1
lim f ( x ) = −1
lim f ( x ) =
x →3
lim f ( x ) = −1
x →0−
lim f ( x ) = 1
x →0+
x2 −1
en x = 2 y en x = 5.
x −5
lim f ( x ) = − ` 
 → No exisste lim f ( x ).
x →5
lim f ( x ) = + `

x → 5+
24
lim f ( x ) →
x →5
0
x → 5−
37
6
lim f ( x ) = − ` 
 → No exisste lim f ( x ).
x →2
lim+ f ( x ) = + `

x →2
x → 2−
lim f ( x ) =
x→4
53
14
Halla los siguientes límites.
a) lim
x →1
x3 − 2x2 + x
x 2 − 3x + 2
a) lim
x →1
x →−2
lim
b)
x 3 − 2x 2 + x
0
→
2
x − 3x + 2
0
b) lim
x →−2
386
si x > 0
si x < 0
x −2
x +3
+
Razona si existe o no el límite de la función f ( x ) =
x +3
x −2
en x = 2, en x = 3 y en x = 4.
5
lim f ( x ) →
x →2
0
023
x →0+
Calcula el límite de la función f ( x ) =
x →2
x
x
lim f ( x ) = + `
x →0
022
x →3
Halla los límites laterales en x = 0 de las funciones.
a) f ( x ) =
021
x → 3+
lim
x → −2
x 4 − 16
x3 + 8
lim
x →1
x 3 − 2x 2 + x
x ( x − 1)2
=0
lim
=
x →1 ( x − 1)( x − 2 )
x2 − 3x + 2
x 4 − 16
0
→
3
x +8
0
8
x 4 − 16
( x 2 + 4 )( x + 2 )( x − 2 )
=−
lim
=
2
3
x
→
−
2
3
x +8
( x + 2 )( x − 2 x + 4 )
SOLUCIONARIO
024
xm −1
si m = 2 y m = 3.
x →1 x − 1
¿Puedes determinar el límite para un valor m cualquiera?
Calcula lim
0
x2 −1
→
x →1 x − 1
0
lim
x2 −1
= lim ( x + 1) = 2
x →1
x −1
lim
x3 −1
0
→
x −1
0
lim
x3 −1
= lim ( x 2 + x + 1) = 3
x →1
x −1
lim
xm −1
= lim (x m−1 + x m−2 + … + x + 1) = m
x →1
x −1
lim
x →1
x →1
025
x →1
x →1
Pon un ejemplo de una función que tenga como asíntotas verticales las rectas
cuyas ecuaciones son:
x=1
x=2
x=3
Respuesta abierta. Por ejemplo: f ( x ) =
026
9
1
( x − 1)( x − 2 )( x − 3 )
Halla las asíntotas verticales de las funciones.
a) f ( x ) =
1
x
b) f ( x ) =
1
x −1
2
c) f ( x ) =
1
x − 4x
3
a) Dom f = R − {0}
lim f ( x ) = − ` 
 → f (x) tiene una asíntota vertical en x = 0.
lim f ( x ) = + `

x → 0+
x → 0−
b) Dom f = R − {−1, 1}
lim f ( x ) = + `
 → f (x) tiene una asíntota vertical en x = −1.
lim + f ( x ) = − ` 

x →−1
lim f ( x ) = − ` 
x →1−
 → f (x) tiene una asíntota vertical en x = 1.
lim+ f ( x ) = + `

x →1
x →−1−
c) Dom f = R − {−2, 0, 2}
lim f ( x ) = − ` 
 → f (x) tiene una asíntota vertical en x = −2.
lim f ( x ) = + `

x →−2+
lim f ( x ) = − ` 
x → 2−
 → f (x) tiene una asíntota vertical en x = 2.
lim+ f ( x ) = + `

x →2
lim f ( x ) = + `
x → 0−
 → f (x) tiene una asíntota vertical en x = 0.
lim+ f ( x ) = − ` 

x →0
x →−2 −
387
Límite de una función
027
¿Puede ocurrir que una función tenga una asíntota horizontal y otra oblicua
cuando x → +`? Razona la respuesta.
No puede ocurrir, ya que si tiene una asíntota horizontal se verifica que: lim f ( x ) = k
x →+ `
f ( x)
Y si lim
= 0 , la función no tiene asíntota oblicua.
x →+ `
x
028
Calcula sus asíntotas y representa las funciones.
a) f ( x ) =
a)
x
b) f ( x ) =
x2 + 1
lim
x →+ `
x2
c) f ( x ) =
x2 + 1
x3
x2 + 1
x
= 0 → f (x) tiene una asíntota horizontal: y = 0.
x +1
2
Y
1
1
b)
lim
x →+ `
X
x2
= 1 → f (x) tiene una asíntota horizontal: y = 1.
x2 + 1
Y
1
1
X

f ( x)
x3
= lim 3
= 1

x → +` x
x → +` x + x
 →
f (x) tiene una asíntota oblicua: y = x.


−x
x3
= 0
− x  = lim 2
 x → + ` x + 1
x2 + 1

lim
c)

lim 
x → + `

Y
1
1
388
X
SOLUCIONARIO
029
9
Estudia la continuidad de estas funciones.
a) f ( x ) = x −2
b) f ( x ) =
x−4
c)
f ( x ) = ln ( 1− x 2 )
a) Dom f = R − {0} → f (x) es continua en R − {0}.
b) Dom f = [4, +`) → f (x) es continua en [4, +`).
c) Dom f = (−1, 1) → f (x) es continua en (−1, 1).
030
Halla m y n para que la función f ( x) sea continua en R.
2
si x ≤ 1

f ( x ) =  mx + n si 1 < x < 3

si x ≥ 3
 4
f (x) es continua en x = 1 si se verifica que: f ( 1) = lim f ( x )
x →1


x →1

lim f ( x ) = m + n → m + n = 2
x →1+


f ( 1) = 2
lim− f ( x ) = 2
f (x) es continua en x = 3 si se verifica que: f (3) = lim f ( x )
x →3
lim f ( x ) = 3 m + n
x → 3−

 → 3 m + n = 4
lim+ f ( x ) = 4

x →3

f (3) = 4

m=1
m + n = 2 
→
3 m + n = 4
n=1
031
Estudia la continuidad de la función que asigna a cada número su parte entera.
y = [x]
Especifica los tipos de discontinuidades que presenta esta función.
La función no es continua para todos los valores enteros. Todos los números
enteros son puntos de discontinuidad inevitable de salto finito.
032
Estudia la continuidad de estas funciones.
 1

x +1
x
a) f ( x ) =
b) f ( x ) = 
x

x −2
5

si x ≤ 1
si 1 < x < 4
si x ≥ 4
a) Dom f = R − {2}
lim f ( x ) = − ` 
 → No existe lim f ( x ) y f(x) no es continua en x = 2.
x →2
lim f ( x ) = + `

x → 2+
x → 2−
La discontinuidad es inevitable de salto infinito. La función tiene una asíntota
vertical en x = 2.
389
Límite de una función
b) Dom f = R − {0}
lim f ( x ) = − ` 
 → No existe lim f ( x ) y f(x) no es continua en x = 0.
x →0
lim+ f ( x ) = + `

x →0
La discontinuidad es inevitable de salto infinito. La función tiene una asíntota
vertical en x = 0.
x → 0−
lim f ( x ) = 1
 → ∃ lim f ( x ) = 1
x →1
lim+ f ( x ) = 1

x →1
Como ∃ f ( 1) = lim f ( x ), la función es continua en x = 1.
x →1−
x →1
lim f ( x ) = 4
 → No existe lim f ( x ) y f(x) no es continua en x = 4.
x→4
lim f ( x ) = 5 

x → 4+
La discontinuidad es inevitable de salto finito.
x → 4−
033
Halla el término general de las sucesiones cuyos primeros términos son:
a) 1, −1, 1, −1, …
b) 1, 2, 4, 8, …
a) an = (−1)n−1
b) an = 2n−1
034
Con ayuda de la calculadora, halla el límite de esta sucesión definida de forma
recurrente.
3an−1 + 2
an =
a1 = 1
4 an−1 + 3
a1 = 1
a2 =
5
= 0 , 71428…
7
a3 =
29
= 0 , 70731…
41
a4 =
169
= 0 , 70711…
239
a5 =
985
= 0 , 707106…
1.393
Los términos de la sucesión se aproximan a:
035
Calcula el límite de la siguiente sucesión con ayuda de la tabla.
n2 − 1
an =
2n +1
n
5
50
500
5.000
50.000
an
2,18
24,74
249,74
2.499,74
24.999,74
lim an = + `
n →`
390
1
= 0 , 7071…
2
SOLUCIONARIO
036
037
9
Comprueba la igualdad con ayuda de la tabla.
4 − 6n
= −3
lim
n→` 2 n + 1
n
5
50
500
5.000
50.000
an
−2,36
−2,93
−2,993
−2,9993
−2,9999
Halla los siguientes límites de sucesiones.
2
2


 2

a) lim  5 n + n − n + 2 
c) lim 2 n − 4 n − 2 n + 7 

n→` 
n→` 
 n−3

n − 1 
2n +1
2

 2
d) lim  6 n + 1 − 9 n − 5 
n→` 
 2n + 4
3 n + 6 
2

 2
b) lim  n − 3 n + 2 − n 
n→` 

n + 3 
3n
 5 n2 + n
n2 + 2 
a) lim 
 → ` − `
−
n→ ` 
 n−3
n − 1 
 5 n2 + n
n2 + 2 
4 n3 − n2 − 3n + 6
 = lim
= +`
lim 
−
n→ `  n − 3
n2 − 4 n + 3
n − 1  n→ `
 n2 − 3 n + 2
n2 
b) lim 
 → ` − `
−
n→ ` 

n + 3 
3n
 n2 − 3 n + 2
n2 
−2 n3 − 7 n + 6
 = lim
= −`
−
lim 
n→ ` 
3n
n + 3  n→ ` 3 n2 + 9 n

4 n2 − 2 n + 7 
c) lim 2 n −
 → ` − `

n→ ` 

2n + 1

4 n2 − 2 n + 7 
4n−7
 = lim
=2
lim 2 n −

→
n→ ` 
n
`

2n + 1
2n + 1
 6 n2 + 1
d) lim 
−
n→ ` 
 2n + 4
 6 n2 + 1
lim 
−
n→ `  2 n + 4
038
9 n2 − 5 
 → ` − `
3 n + 6 
9 n2 − 5 
13
 = lim
=0
3 n + 6  n→ ` 6 ( n + 2 )
Obtén los resultados de:
a) lim
n→`
4 n2 + n − 3
3n + 1
a) lim
n→ `
b) lim
n→ `
c) lim
n →`
b) lim
n→`
4 n2 + n − 3
`
→
3n + 1
`
8 n2 + 3 n + 2
n3 + 2 n4
→
`
`
8n2 + 3 n + 2
n3 + 2 n 4
lim
n →`
lim
n →`
c) lim
n→`
5 − 2 n + 6 n3
n2 − n − 6
4 n2 + n − 3
2
=
3n + 1
3
8 n2 + 3 n + 2
n3 + 2 n4
=
8
2
=4 2
5 − 2 n + 6 n3
=0
n2 − n − 6
391
Límite de una función
039
Determina los límites.
a) lim (n − n2 + 4 n − 1 )
n→`
b) lim ( 4 n2 + n + 31 − 3 n)
n→`
c) lim ( 4 n − 16 n2 + 2 )
n→`
a) lim (n − n2 + 4 n − 1 ) → ` − `
n→ `
lim (n − n2 + 4 n − 1 ) = lim
n→ `
n→ `
−4 n + 1
n + n2 + 4 n − 1
= −2
b) lim ( 4 n2 + n + 31 − 3 n) → ` − `
n→ `
−5 n2 + n + 31
lim ( 4 n2 + n + 31 − 3 n) = lim
n→ `
n→ `
4 n2 + n + 31 + 3n
= −`
c) lim ( 4 n − 16 n2 + 2 ) → ` − `
n→ `
lim ( 4 n − 16 n2 + 2 ) = lim
n→ `
040
4 n + 16 n2 + 2
=0
Halla los siguientes límites.
a)
lim x 3 + 2 x 2 − 3
x →+ `
b) lim
x →−`
a)
1
lnx
c)
lim
x →−`
4
x + 2x + 1
2
d) lim xe x
x →+`
lim ( x 3 + 2 x 2 − 3 ) = + `
x → +`
b) lim
x →− `
041
n→ `
−2
1
=0
lnx
c)
lim
x →− `
d)
4
=0
x + 2x + 1
2
lim xe x = + `
x → +`
Representa las funciones.
f (x) = 2 x − 3
g( x ) = x 2 + 2 x −1
A partir de la gráfica,
calcula los siguientes límites.
a)
lim f ( x )
x →−`
b) lim g( x )
x →−`
Y
c)
lim f ( x )
x →+ `
d) lim g( x )
x →+ `
g(x)
f(x)
1
2
a) lim f ( x ) = − `
c) lim f ( x ) = + `
b) lim g( x ) = + `
d) lim g( x ) = + `
x →−`
x →−`
392
x →+ `
x →+ `
X
SOLUCIONARIO
042
Calcula.
a)
lim (x 3 − 3 x 2 )
x →+ `
b) lim ( x 4 + 2x 3 + x 2 −17x )
x →+ `
a)
b)
c)
d)
043
lim ( −2 x 4 + 8x 3 − 3 x 2 + 27x − 42 )
x →+ `
d) lim ( 1− 3 x 3 + 5 x 2 − 6x )
x →+ `
lim ( x 3 − 3x 2 ) = + `
x → +`
lim ( x 4 + 2 x 3 + x 2 − 17x ) = + `
x → +`
lim (−2 x 4 + 8 x 3 − 3 x 2 + 27x − 42 ) = − `
x → +`
lim ( 1− 3x 3 + 5 x 2 − 6 x ) = − `
x → +`
lim ( 6x 3 + x 2 )
x →−`
b) lim ( x 4 + 4 x 3 + 7x 2 −12 x + 1)
x →−`
a)
b)
c)
d)
c)
lim ( 5 x 3 − 3 x 2 −16x + 3 )
x →−`
d) lim ( 7 − 12 x + 3 x 2 + 9x 3 )
x →−`
lim ( 6 x 3 + x 2 ) = − `
x → −`
lim ( x 4 + 4 x 3 + 7x 2 − 12 x + 1) = + `
x → −`
lim (5x 3 − 3x 2 − 16 x + 3 ) = − `
x → −`
lim (7 − 12 x + 3 x 2 + 9 x 3 ) = − `
x → −`
Halla los límites.
a) lim −2 t 2 + 5
t →+ `
a)
045
c)
Determina los límites.
a)
044
9
lim −2 t 2 + 5= + `
t → +`
b) lim t 3 + 6 t + 3
t →−`
b) lim t 3 + 6 t + 3= + `
t → −`
Calcula los límites, y comprueba el resultado con tu calculadora.
2 x 2 − 6x + 3
4 x 2 + x −12
a) lim
d)
lim
x →+ ` x 2 − 3x + 5
x →+ ` x 2 − x 3 + 2
2 x 2 − 6x 3 − x + 1
1+ x − 6x 4 + x 3
b) lim
e)
lim
x →+ `
x →+ `
4 x 2 + 5x − 2
3x + 2 x 2 − 3
c)
lim
x →+ `
a)
b)
c)
5 x 3 + 3x −1
6x 2 −3x 3 + x
lim
2x 2 − 6 x + 3
=2
x 2 − 3x + 5
d)
lim
2x2 − 6x3 − x + 1
= −`
4 x 2 + 5x − 2
e)
lim
5x 3 + 3x − 1
5
=−
2
3
6 x − 3x + x
3
x → +`
x → +`
x → +`
lim
x → +`
4 x 2 + x − 12
=0
x2 − x3 + 2
1+ x − 6 x 4 + x 3
= −`
x → +`
3x + 2 x 2 − 3
lim
393
Límite de una función
046
Halla estos límites con ayuda de la calculadora, y comprueba el resultado obtenido.
a)
lim
x →−`
b) lim
x →−`
a)
b)
047
x 2 + 5x + 7
c)
2x2 + x + 1
4 + x −2x3
x →−`
lim
x 2 + 5x + 7
1
=
2
2x + x + 1
2
lim
4 + x − 2 x3
= +`
2 x 2 − 3 x + 11
x → −`
lim
x →−`
d) lim
2 x 2 − 3x + 11
x → −`
x 3 − 2 x 2 −10x
−x 2 + 2 x 3 − x + 3
−x 2 + 3 x + 21
5x 2 − 4 x 3 + 2 x
x 3 − 2 x 2 − 10 x
1
=
x → −` − x 2 + 2 x 3 − x + 3
2
2
− x + 3x + 21
=0
d) lim
x →− ` 5 x 2 − 4 x 3 + 2 x
c)
lim
Escribe, en cada caso, un polinomio, P(x), para obtener los resultados indicados
cuando calculamos el límite.
8 x 2 + 6 x −1
lim
x →+`
P(x)
a) 4
b) 5
d) + `
c) 0
e) −`
f) 1
Respuesta abierta.
a) P(x) = 2x 2 + x + 1
8
b) P(x) = x2 + x + 1
5
048
lim
x →+ `
a)
(
4 x 2 + 2 x − 4 x 2 −3 )
d) P(x) = x + 1
f ) P(x) = 8x 2
b)
b) lim
x →+ `
(
x 2 −2x + 1 − x 2 −2x + 4 )
lim
(
4 x 2 + 2x −
4x2 − 3 ) → ` − `
lim
(
4 x 2 + 2x −
4 x 2 − 3 ) = lim
lim
(
x 2 − 2x + 1 −
x 2 − 2x + 4 ) → ` − `
lim
(
x 2 − 2x + 1 −
x 2 − 2x + 4 ) =
−3
x → +`
x → +`
x → +`
x → +`
= lim
x → +`
2x + 3
x → +`
x2 − 2x + 1 +
4 x 2 + 2x +
x 2 − 2x + 4
4x2 − 3
=0
Halla los límites.
a)
 5x 2 + 1
3 − x2
lim 
+
x →−` 
x
x+2
a)
394
e) P(x) = −1
Encuentra el valor de:
a)
049
c) P(x) = 2x 3 + x



 5x 2 + 1 3 − x 2
lim 
+
x → −` 
x
x+2
 5x 2 + 1 3 − x 2
lim 
+
x → −` 

x
x+2

2 x 2 + 1 
x3

b) lim 
−
x →−` 
2 x − 4 
 x2 −2 x

 → ` − `


4 x 3 + 10 x 2 + 4 x + 2
 = lim
= −`
 x → −`
x 2 + 2x
=
1
2
9
SOLUCIONARIO
 x3
2 x 2 + 1 
 → ` − `
lim  2
−
x → −`  x − 2 x
2 x − 4 
b)
 x3
2 x 2 + 1 
−x
 = lim
−
=0
lim  2
2
x → −`  x − 2 x
2 x − 4  x → −` 2 x − 4 x
050
Obtén los resultados de:
a)
lim
x →−`
a)
051
−3x + 6 x 2
x2 + 2
x → −`
2 x 4 + 5x 3 − 2 x 2
x →−`
−3 x + 6 x 2
=0
x2 + 2
lim
3 x −1
b)
lim
x → −`
2x 4 + 5x 3 − 2x 2
= −`
3x − 1
Determina.
a) lim 2 − x + 4
x →0
x
a) lim
lim
x →2
lim
x →2
x →2
x − 2
x −2
x+4
0
→
x
0
2−
−x
x+4
−1
1
= lim
= lim
=−
→
0
→
0
x
x
x
4
2+ x + 4
x (2 + x + 4 )
x →0
b) lim
b) lim
2−
x →0
052
b) lim
x − 2
0
→
x −2
0
x − 2
x −2
= lim
= lim
x
x →2
→
2
x −2
( x − 2 )( x + 2 )
1
x + 2
=
1
2 2
=
2
4
Determina los límites, calculando previamente sus límites laterales.
a) lim
x →2
x 2 − 3x + 2
2x − 5
b) lim ( 1 + 2 x) x
x →3
c) lim
x2 − 2x + 3
x →0
x +1
d) lim
x →−1
f ) lim
x →−3
x →3
x →0
5
4+x
d) lim 4 − 2 x = 2
x →−1 x 2 − 2 x
 x + 1 
= 0
e) lim ln 
x →2
 3 
b) lim ( 1 + 2 x ) x = 343
x 2 − 2x + 3
=
x +1
x 2 − 2x
 x + 1

e) lim ln 
 3 
x →2
2
a) lim x − 3x + 2 = 0
x →2
2x − 5
c) lim
4 − 2x
3
f)
lim
x →−3
5
4+x
=5
395
Límite de una función
053
054
Con ayuda de la calculadora, completa la tabla y comprueba que
x2
si f ( x ) =
, entonces lim f ( x ) = −0 , 5.
x →1
x −3
x
0
0,9
0,99
0,999
1,001
1,01
1,1
f (x)
0
−0,38
−0,48
−0,49
−0,501
−0,51
−0,63
Calcula los límites indicados en la función.
2 x + 4
g( x ) =  2
 x − 2 x + 1
si x ≥ 4
a) lim g ( x )
c) lim− g( x )
e) lim+ g ( x )
b) lim− g ( x )
d) lim g ( x )
f ) lim+ g ( x )
x →−3
x →6
x→4
x →6
x→4
x →3
a) lim g ( x ) = lim ( 2 x + 4 ) = −2
d) lim g ( x ) = lim ( 2 x + 4 ) = 10
b) lim g ( x ) = lim ( x 2 − 2 x + 1) = 25
−
−
e) lim g ( x ) = lim ( x 2 − 2 x + 1) = 25
+
+
c)
f ) lim g ( x ) = lim ( x 2 − 2 x + 1) = 9
+
+
x →−3
x →6
055
si x < 4
x →−3
x →3
x →6
x →6
lim g ( x ) = lim− ( 2 x + 4 ) = 12
x → 4−
x→4
x→4
x →3
x →6
x→4
Observa las gráficas de las funciones f(x) y g(x), y halla los siguientes límites.
a) lim− f ( x )
Y
x →1
lim f ( x )
x →1+
1
f (x)
X
1
Y
b) lim− g ( x )
x →1
lim g ( x )
x →1+
1
g(x)
1
a) lim f ( x ) = + `
−
x →1
lim f ( x ) = + `
x →1+
396
b) lim g ( x ) = − `
−
x →1
lim g ( x ) = + `
x →1+
X
SOLUCIONARIO
056
Determina los límites, y si es preciso, calcula los límites laterales.
a) lim
x2 + 6
x −2
c) lim
b) lim
3
9 − x2
d) lim
x →2
x →3
x →2
4 − 2x
2
x − 2x + 1
lim−
x2 + 6
= −`
x −2
lim−
3
= +`
9 − x2
lim−
x 2 + 2x
= +`
8 − 2x
lim−
4 − 2x
= +`
x − 2x + 1
x →2
3
3
→
x →3 9 − x 2
0
x →3
c) lim
x 2 + 2x
24
→
8 − 2x
0
d) lim
4 − 2x
2
→
x − 2x + 1
0
x→4
2
x →1
8 − 2x
x →1
b) lim
x→4
x2 + 2x
x→4
x2 + 6
10
→
x −2
0
a) lim
057
9
x →1
2
lim+
x2 + 6
= +`
x −2
lim+
3
= −`
9 − x2
lim+
x 2 + 2x
= −`
8 − 2x
lim+
4 − 2x
= +`
x − 2x + 1
x →2
x →3
x→4
x →1
2
Halla los límites.
a) lim cos x
b) lim tg x
x →π
x→
c)
π
d) lim
lim sen x
x→
x →π
3π
2
cos x
sen x
2
a) lim cos x = −1
x →π
b) lim tg x →
x→
c)
π
2
lim− tg x = + `
x→
π
2
lim+ tg x = − `
x→
π
2
lim sen x = −1
x→
3π
2
d) lim
x →π
058
1
0
cos x
sen x
→−
1
0
lim−
x →π
cos x
sen x
= −`
lim+
x →π
cos x
sen x
= +`
Dada la función f(x) definida a trozos, encuentra los límites.
 2 x + 1

 9
f (x) = 
 x − 1
 2
 x + 6x − 32
a) lim f ( x )
c)
b) lim f ( x )
d)
x →−`
x →+`
a)
b)
c)
lim f ( x )
x →−2−
si x < −2
si −2 ≤ x < 3
si x ≥ 3
e) lim f ( x )
g) lim f ( x )
+
f ) lim f ( x )
−
h) lim f ( x )
x →−2
lim f ( x )
x →−2+
d)
lim f ( x ) = + `
e) lim f ( x ) = −3
lim f ( x ) = −3
9
f ) lim f ( x ) =
−
x →3
2
x →+`
x →−2−
x →3
x →3
lim f ( x ) = − `
x →−`
x →3
lim f ( x ) = −3
x →−2+
x →−2
g) lim f ( x ) = −5
+
x →3
h) lim f ( x ) no existe .
x →3
397
Límite de una función
059
Calcula los límites laterales y el siguiente límite.
x2 − x − 6
lim 2
x →3 x − 6x + 9
lim
x2 − x − 6
0
→
2
x − 6x + 9
0
lim
x2 − x − 6
x+2
5
( x − 3 )( x + 2 )
→
= lim
= lim
2
2
x
x
→
→
3
3
x − 6x + 9
x −3
0
( x − 3)
x →3
x →3

x2 − x − 6
= + ` 
2

x2 − x − 6
x →3 x − 6 x + 9
→
lim
= +`

x →3 x 2 − 6 x + 9

x2 − x − 6
lim 2
= + `
x → 3+ x − 6 x + 9

lim−
060
Resuelve los límites.
a) lim
x →−3
b) lim
x →2
c) lim
x →−4
( 2 x − 3 )( x + 3 )
x 3 − 9x 2 + 15x + 25
d) lim
x →5
( x + 1)( x + 3 )
2 x 2 − 9x + 10
x 3 − 5x 2 + 2x − 10
2 x 2 − 11x + 14
4x 2 − 16x + 16
e) lim
3 x 2 − 7x + 2
x →2
3 x 3 + 12 x 2 − x − 4
x 3 + 7x 2 + 14x + 8
f ) lim
x →−1
x3 + x2 − x −1
x3 + 2x2 + x
a) lim ( 2 x − 3 )( x + 3 ) → 0
x →−3 ( x + 1)( x + 3 )
0
9
( 2 x − 3 )( x + 3 )
2x − 3
=
= lim
x →−3 ( x + 1)( x + 3 )
x →−3 x + 1
2
lim
b) lim
x →2
lim
x →2
2 x 2 − 9 x + 10
0
→
2
3x − 7 x + 2
0
( x − 2 )( 2 x − 5 )
2 x 2 − 9 x + 10
2x − 5
1
= lim
=−
= lim
2
x → 2 ( x − 2 )( 3 x − 1)
x → 2 3x − 1
3 x − 7x + 2
5
c) lim
x →−4
lim
3 x 3 + 12 x 2 − x − 4
0
→
3
2
x + 7 x + 14 x + 8
0
3 x 3 + 12 x 2 − x − 4
x →−4
x 3 + 7 x 2 + 14 x + 8
= lim
x →−4
= lim
x →−4
d) lim
x →5
lim
x →5
398
( x + 4 )( 3 x 2 − 1)
( x + 4 )( x 2 + 3 x + 2 )
=
3x 2 − 1
47
=
2
x + 3x + 2
6
x 3 − 9 x 2 + 15x + 25
0
→
3
2
x − 5x + 2 x − 10
0
x 3 − 9 x 2 + 15 x + 25
x 3 − 5x 2 + 2 x − 10
= lim
x →5
( x − 5 )(( x 2 − 4 x − 5 )
( x − 5 )( x 2 + 2 )
= lim
x →5
x2 − 4x − 5
x2 + 2
=0
SOLUCIONARIO
e) lim
x →2
lim
x →2
9
2 x 2 − 11 x + 14
0
→
2
4 x − 16 x + 16
0
2x − 7
3
2 x 2 − 11 x + 14
( x − 2 )( 2 x − 7 )
= lim
→−
= lim
2
→
2
x
x
→
2
4x − 8
0
( x − 2 )( 4 x − 8 )
4 x − 16 x + 16
lim−
x →2
2 x 2 − 11 x + 14
= +`
4 x 2 − 16 x + 16
lim+
x →2
2 x 2 − 11x + 14
= −`
4 x 2 − 16 x + 16
x3 + x2 − x −1
0
→
3
2
x →−1 x + 2 x + x
0
f ) lim
x −1
x3 + x2 − x −1
( x + 1)2 ( x − 1)
= lim
=2
lim
=
2
3
2
x →−1
x →−1 x + 2 x + x
x →−1
x ( x + 1)
x
lim
061
Dada la función:
f (x) =
2 x 2 + 3x − 2
x2 − 4
determina los siguientes límites.
a) lim f ( x )
b) lim f ( x )
x →+ `
a)
c)
x →1
lim f ( x )
x →−`
d) lim f ( x )
x →−2
lim f ( x ) = 2
x →+ `
b) lim f ( x ) = −1
x →1
c)
lim f ( x ) = 2
x → −`
0
0
2
2x − 1
5
2 x + 3x − 2
( x + 2 )( 2 x − 1)
=
= lim
lim
= lim
2
x →−2 x − 2
x →−2
x →−2 ( x + 2 )(( x − 2 )
4
x −4
d) lim f ( x ) →
x →−2
062
Encuentra el límite de la función cuando x tiende a 0 y cuando x tiende a 3.
x4
x 3 − 3x 2
Especifica el valor de los límites laterales, si es necesario.
f (x) =
lim
0
x4
→
3
2
x − 3x
0
lim
81
x4
→
3
2
x − 3x
0
x →0
x →3
lim
x →0
x4
x2
=
=0
lim
x →0 x − 3
x 3 − 3x 2
x4

= − ` 
3
2

x →3 x − 3x
x4
.
→ No existe lim 3

x →3 x − 3 x 2

x4
lim 3
= + `
2
x → 3+ x − 3 x

lim−
399
Límite de una función
063
Determina el límite, y comprueba el resultado con la calculadora.
 3x 2 − 4 x

lim 
− 3 x 

x →+` 
x+2
 3x 2 − 4 x

lim 
− 3 x  → ` − `

x→ +` 
x+2

 3x 2 − 4 x
−10 x
= −10
− 3x  = lim
lim 
 x → + ` x + 2
x→ +` 
x+2
064
Observa las tablas de valores de la función.
4 x 2 − 5x
f (x) =
2x2 + 7
x
1
10
100
1.000
10.000
f (x)
−0,11
1,69
1,974
1,9975
1,99975
x
−1
1
−10
2,17
−100
2,024
−1.000
2,0025
−10.000
2,00025
f (x)
¿Es cierto que y = 2 es una asíntota? Cuando x tiende a + `, ¿está la función por
encima o por debajo de la asíntota? ¿Qué sucede cuando x tiende a −`?
Sí, es cierto que y = 2 es una asíntota horizontal.
Cuando x tiende a +`, la función está por debajo de la asíntota.
Cuando x tiende a −`, la función está por encima de la asíntota.
065
Decide si la función y =
respecto de esa asíntota.
lim
x → +`
3 − 2x
tiene alguna asíntota horizontal, y sitúa la función
x +1
3 − 2x
= −2 → La función tiene una asíntota horizontal: y = −2.
x +1
Si x = 1.000, f (x) > −2, y cuando x tiende a +` la función está por encima
de la asíntota.
Si x = −1.000, f (x) < −2, y cuando x tiende a −` la función está por debajo
de la asíntota.
066
Observa las tablas de valores de la función.
f (x) =
400
3x + 1
x −3
x
2
2,5
2,9
2,99
2,999
2,9999
f (x)
−7
−17
−97
−997
−9.997
−99.997
x
3,0001
3,001
3,01
3,1
3,5
f (x)
100.003
10.003
1.003
103
23
SOLUCIONARIO
9
¿Es cierto que x = 3 es una asíntota vertical? Cuando x tiende a 3 por la izquierda,
¿la rama infinita de la función tiende a + ` o −`? ¿Qué sucede cuando x tiende
a 3 por la derecha?
Sí, es cierto que x = 3 es una asíntota vertical.
Cuando x tiende a 3 por la izquierda, la rama infinita de la función tiende a −`.
Cuando x tiende a 3 por la derecha, la rama infinita de la función tiende a +`.
067
1
tiene alguna asíntota vertical,
x − 3x − 4
y estudia sus ramas infinitas próximas a esas asíntotas.
Decide si la función y =
2
Dom f = R − {−1, 4}
1
1
lim 2
→
x →−1 x − 3 x − 4
0

1
= + `
x →−1 x − 3 x − 4

 → La función tiene una asíntota vertical en x = −1.

1
lim+ 2
= −`


x →−1 x − 3 x − 4


Por la izquierda la rama infinita de la función tiende a +`, y por la derecha, a −`.
lim −
lim
x→4
2
1
1
→
x − 3x − 4
0
2
1

= − ` 
x → 4 x − 3x − 4

 → La función tiene una asíntota vertical en x = 4.

1

= + `
lim 2

x → 4+ x − 3 x − 4


Por la izquierda la rama infinita de la función tiende a −`, y por la derecha, a +`.
lim−
068
2
Observa la tabla de valores de la función.
f (x) =
4x 2 + 6x
2x − 3
x
10
100
1.000
10.000
f (x)
27,06
206,09
2.006,009
20.006,0009
Esta es la tabla de valores de la recta y = 2x + 6.
x
10
100
1.000
10.000
y = 2x + 3
26
206
2.006
20.006
¿Es cierto que la recta es una asíntota de la otra función?
¿Qué posición tienen cuando x tiende a + `? Investiga la posición relativa
de ambas cuando x tiende a −`.
Sí, es cierto que y = 2x + 3 es una asíntota oblicua.
Cuando x tiende a +`, la función está por encima de la asíntota.
Si x = −1.000, f (x) − 2x − 3 > 0, y cuando x tiende a −` la función está
por encima de la asíntota.
401
Límite de una función
069
Comprueba si la recta y = x + 3 es una asíntota oblicua de la función y =
En caso afirmativo, decide la posición que ocupa una respecto de la otra.
x 2 + 5x
.
x +2
f ( x)
x 2 + 5x

= lim 2
=1

x → +` x
x → +` x + 2 x
 → La función tiene una asíntota

 x 2 + 5xx


3x


oblicua: y = x + 3.

lim 
= 3
− x  = lim
 x → + ` x + 2
x → + ` x + 2

lim
Si x = 1.000, f (x) − x − 3 < 0, y cuando x tiende a +` la función está
por debajo de la asíntota.
Si x = −1.000, f (x) − x − 3 > 0, y cuando x tiende a −` la función está
por encima de la asíntota.
070
Calcula las asíntotas oblicuas de las funciones y su posición relativa respecto de ellas.
2x2 + 4
2x2 + 4
a) f ( x ) =
b) f ( x ) =
2+ x
x −1

f ( x)
2x 2 + 4

= lim
=
2
x → +` x
x → +` x 2 − x

a)
 → La función tiene una asíntota

 2x 2 + 4

4 + 2x

oblicua: y = 2x + 2.
− 2 x  = lim
= 2
lim 
 x → + ` x − 1
x → + `
 x −1

lim
Si x = 1.000, f (x) − 2x − 2 > 0, y cuando x tiende a +` la función está
por encima de la asíntota.
Si x = −1.000, f (x) − 2x − 2 < 0, y cuando x tiende a −` la función
está por debajo de la asíntota.

f ( x)
2x 2 + 4

= lim
=
2
x → +` x
x → +` 2x + x 2

b)
 → La función tiene una asíntota

 2x 2 + 4

4 − 4x

oblicua: y = 2x − 4.
= −4
lim 
− 2 x  = lim
 x → + ` x − 1
x → + `
 2+ x

lim
Si x = 1.000, f (x) − 2x + 4 > 0, y cuando x tiende a +` la función está
por encima de la asíntota.
Si x = −1.000, f (x) − 2x + 4 < 0, y cuando x tiende a −` la función
está por debajo de la asíntota.
071
Determina todas las asíntotas de las funciones, y sitúa sus ramas infinitas.
a) f ( x ) =
2 − 6x
x +3
d) f ( x ) =
3
x −1
b) f ( x ) =
3x 2 + 2 x
x +1
e) f ( x ) =
x3
x 2 − 5x + 6
f ) f (x) =
x
x + x +1
c) f ( x ) =
402
4x 3
x −5
2
SOLUCIONARIO
9
2 − 6x
20
→
x →−3 x + 3
0
a) lim

2 − 6x
= − ` 

x →−3
x+3
 → La función tiene una asíntota vertical en x = −3.

2 − 6x
lim
= + `

x →−3+ x + 3
Por la izquierda la rama infinita de la función tiende a −`, y por la derecha, a +`.
lim −
lim
x→ +`
2 − 6x
= −6 → La función tiene una asíntota horizontal: y = −6.
x+3
Si x = 1.000, f (x) > −6, y cuando x tiende a +` la función está
por encima de la asíntota.
Si x = −1.000 → f (x) < −6, y cuando x tiende a −` la función
está por debajo de la asíntota.
Al tener una asíntota horizontal, la función no tiene asíntota oblicua.
3x 2 + 2 x
1
→
x →−1
x +1
0
b) lim

3x 2 + 2 x
= − ` 

x →−1
x +1
 → La función tiene una asíntota vertical en x = −1.
2

3x + 2 x
lim +
= + `

x →−1
x +1
Por la izquierda la rama infinita de la función tiende a −`, y por la derecha, a +`.
3x 2 + 2 x
lim
= + ` → La función no tiene asíntota horizontal.
x → +`
x +1
3x 2 + 2 x
f(x)

= lim
=3
lim

2
`
→
+
x → +`
x
x +x
x

 → La función tiene una asíntota

 3x 2 + 2 x

−
x
oblicua: y = 3x −1.
= −1
− 3 x  = lim
lim 

x → + `
 x → + ` x + 1
x +1

Si x = 1.000, f (x) − 3x + 1 > 0, y cuando x tiende a +` la función está
por encima de la asíntota.
Si x = −1.000, f (x) − 3x + 1 < 0, y cuando x tiende a −` la función
está por debajo de la asíntota.
lim −
4x3
500
→
x →5 x − 5
0
3

4x
= − ` 
lim−

x →5 x − 5
 → La función tiene una asíntota vertical en x = 5.

4x3
lim+
= + `
x →5 x − 5

Por la izquierda la rama infinita de la función tiende a −`, y por la derecha, a +`.
c) lim
lim
4x3
= + ` → La función no tiene asíntota horizontal.
x −5
lim
4x3
= + ` → La función no tiene asíntota oblicua.
x 2 − 5x
x → +`
x → +`
403
Límite de una función
d) lim
x →1
3
3
→
x −1
0

3
= − ` 

x →1 x − 1
 → La función tiene una asíntota vertical en x = 1.

3
= + `
lim+
x →1 x − 1

lim−
Por la izquierda la rama infinita de la función tiende a −`, y por la derecha, a +`.
lim
x → +`
3
= 0 → La función tiene una asíntota horizontal: y = 0.
x −1
Si x = 1.000, f (x) > 0, y cuando x tiende a +` la función está
por encima de la asíntota.
Si x = −1.000, f (x) < 0, y cuando x tiende a −` la función
está por debajo de la asíntota.
Al tener una asíntota horizontal, la función no tiene asíntota oblicua.
e) lim
x →2
8
x3
→
2
x − 5x + 6
0

x3
= + `

x → 2 x − 5x + 6
 → La función tiene una asíntota vertical en x = 2.
3

x
= − ` 
lim 2
x → 2+ x − 5 x + 6

lim−
2
Por la izquierda la rama infinita de la función tiende a +`, y por la derecha, a −`.
lim
x →3
27
x3
→
2
x − 5x + 6
0

x3
= − ` 
2

x → 3 x − 5x + 6
 → La función tiene una asíntota vertical en x = 3.
3

x
= + `
lim+ 2
x → 3 x − 5x + 6

lim−
Por la izquierda la rama infinita de la función tiende a −`, y por la derecha, a +`.
lim
x → +`
x3
= + ` → La función no tiene asíntota horizontal.
x 2 − 5x + 6

x3
=1

3
2
x → +` x
x → + ` x − 5x + 6x
 → La función tiene una

3
2



x
5
6
−
x
x
lim  2
− x  = lim 2
= 5 asíntota oblicua:
 y = x + 5.
 x → + ` x − 5x + 6
x → + ` x − 5 x + 6

lim
f ( x)
= lim
Si x = 1.000, f (x) − x − 5 > 0, y cuando x tiende a +` la función está
por encima de la asíntota.
Si x = −1.000, f (x) − x − 5 < 0, y cuando x tiende a −` la función
está por debajo de la asíntota.
404
SOLUCIONARIO
9
f ) Dom f = R → La función no tiene asíntota vertical.
lim
x → +`
x
= 0 → La función tiene una asíntota horizontal: y = 0.
x + x +1
2
Si x = 1.000, f (x) > 0, y cuando x tiende a +` la función está
por encima de la asíntota.
Si x = −1.000, f (x) < 0, y cuando x tiende a −` la función
está por debajo de la asíntota.
Al tener una asíntota horizontal, la función no tiene asíntota oblicua.
072
Obtén todas las ramas infinitas y las asíntotas de las funciones, y decide la posición
que tienen entre sí.
a) f ( x ) =
b) f ( x ) =
c) f ( x ) =
d) f ( x ) =
x 3 − 7x + 1
2 x 2 − 5x 3
x 3 − 7x + 1
2x2 − 8
x 3 − 7x + 1
2x2 + 8
x 3 − 7x + 1
2x + 8
 2 
a) Dom f = R − 0 , 
 5 
lim
x →0
x 3 − 7x + 1
1
→
2
3
2 x − 5x
0

x 3 − 7x + 1

=
+
`

x →0
2x 2 − 5x 3
 → La función tiene una asíntota vertical en x = 0.

x 3 − 7x + 1
lim+
=
+

`
x →0
2 x 2 − 5x 3

lim−
Las dos ramas infinitas de la función tienden a +`.
lim
x→
2
5
x 3 − 7x + 1
−1, 736
→
2
3
2 x − 5x
0

x 3 − 7x + 1

=
−
`
2
3

2
−
2
x
5
x
x→

2
5
 → La función tiene una asíntota vertical en x = .

x 3 − 7x + 1
5
= + `
lim+
3
2

2
x
2
−
x
5

x→
5

lim−
Por la izquierda la rama infinita de la función tiende a −`,
y por la derecha tiende a +`.
405
Límite de una función
lim
x → +`
x 3 − 7x + 1
1
1
= − → La función tiene una asíntota horizontal: y = − .
2
3
2 x − 5x
5
5
1
Si x = 1.000, f ( x ) < − , y cuando x tiende a +` la función está
5
por debajo de la asíntota.
1
Si x = −1.000, f ( x ) > − , y cuando x tiende a −` la función
5
está por encima de la asíntota.
Al tener una asíntota horizontal, la función no tiene asíntota oblicua.
b) Dom f = R − {−2, 2}
lim
x →−2
x 3 − 7x + 1
7
→
2
2x − 8
0

x 3 − 7x + 1

=
+
`

x →−2
2x2 − 8
 → La función tiene una asíntota vertical en x = −2.
3

x − 7x + 1
lim +
= − ` 
2
x →−2
2x − 8

lim −
Por la izquierda la rama infinita de la función tiende a +`,
y por la derecha tiende a −`.
lim
x →2
x 3 − 7x + 1
−5
→
2
2x − 8
0

x 3 − 7x + 1

=
+
`

x →2
2x 2 − 8
 → La función tiene una asíntota vertical en x = 2.

x 3 − 7x + 1
=
−
lim+

`
x →2
2x 2 − 8

lim−
Por la izquierda la rama infinita de la función tiende a +`,
y por la derecha tiende a −`.
lim
x → +`
x 3 − 7x + 1
= + ` → La función no tiene asíntota horizontal.
2x 2 − 8
 La función tiene
f ( x)
x 3 − 7x + 1
1
lim
= lim
=

x → +` x
x → + ` 2x 3 − 8 x
2
 → una asíntota oblicua:

 x 3 − 7 x + 1 1 

1
−3 x + 1

y = x.
lim 
=
0
−
x
lim
=


2
2

x → + `
2x − 8
2  x → + ` 2 x − 8
2

1
Si x = 1.000, f ( x ) − x < 0 , y cuando x tiende a +` la función está
2
por debajo de la asíntota.
1
x > 0 , y cuando x tiende a −` la función
2
está por encima de la asíntota.
Si x = −1.000, f ( x ) −
406
SOLUCIONARIO
9
c) Dom f = R → La función no tiene asíntota vertical.
x 3 − 7x + 1
= + ` → La función no tiene asíntota horizontal.
x → +`
2x2 + 8

f ( x)
x 3 − 7x + 1
1
La función tiene
= lim
=
lim

3
x → +` x
x → +` 2 x + 8 x
2
 → una asíntota oblicua:

 x 3 − 7x + 1 1 

1
−11x + 1

y = x.
lim 
=
0
lim
=
x
−


2
2

x → + `
x
→
+
`
2x + 8
2x + 8
2 
2

lim
1
x < 0 , y cuando x tiende a +` la función está
2
por debajo de la asíntota.
Si x = 1.000, f ( x ) −
1
x > 0 , y cuando x tiende a −` la función
2
está por encima de la asíntota.
Si x = −1.000, f ( x ) −
d) Dom f = R − {−4}
x 3 − 7x + 1
−35
lim
→
x →−4
2x + 8
0

x 3 − 7x + 1
= + `
lim −

x →−4
2x + 8
 → La función tiene una asíntota vertical en x = −4.

x 3 − 7x + 1
= − ` 
lim +

x →−4
2x + 8
Por la izquierda la rama infinita de la función tiende a +`, y por la derecha
tiende a −`.
lim
x → +`
lim
x → +`
073
x 3 − 7x + 1
= + ` → La función no tiene asíntota horizontal.
2x + 8
f ( x)
x
= lim
x → +`
x 3 − 7x + 1
= + ` → La función no tiene asíntota oblicua.
2x2 + 8 x
Halla las asíntotas de estas funciones, y la posición de las ramas infinitas.
a) f ( x ) =
x 3 − 6x 2 + 12 x − 8
x +3
d) f ( x ) =
x 3 − 6 x 2 + 12 x − 8
x2 − 4
b) f ( x ) =
x 3 − 6x 2 + 12 − 8
x2 + x −6
e) f ( x ) =
x 3 − 6x 2 + 12 x − 8
( x − 2 )2
c) f ( x ) =
x 3 − 6x 2 + 12 x − 8
x −2
f ) f (x) =
x 3 − 6x 2 + 12 x − 8
x2 + 4
a) Dom f = R − {−3}
x 3 − 6 x 2 + 12 x − 8
−125
lim
→
x →−3
x+3
0

x 3 − 6 x 2 + 12 x − 8
= + `

x →−3
x+3
→

x 3 − 6 x 2 + 12 x − 8
= − ` 
lim +
x →−3
x+3

lim −
La función tiene una asíntota vertical
en x = −3. Por la izquierda la rama
infinita de la función tiende a +`,
y por la derecha tiende a −`.
407
Límite de una función
lim
x → +`
x 3 − 6 x 2 + 12 x − 8
= + ` → La función no tiene asíntota horizontal.
x+3
f ( x)
lim
x → +`
x
oblicua.
= lim
x → +`
x 3 − 6 x 2 + 12 x − 8
= + ` → La función no tiene asíntota
x 2 + 3x
b) Dom f = R − {−3, 2}
x 3 − 6 x 2 + 12 x − 8
−125
→
2
x + x −6
0
lim
x →−3

x 3 − 6 x 2 + 12 x − 8
= − ` 
2

x →−3
x + x −6
 → La función tiene una asíntota vertical
3
2

x − 6 x + 12 x − 8
= + `
lim +
2
x →−3
x + x −6

en x = −3. Por la izquierda la rama infinita de la función tiende a −`,
y por la derecha tiende a +`.
lim −
lim
x →2
x 3 − 6 x 2 + 12 x − 8
0
→
2
x + x −6
0
x 3 − 6 x 2 + 12 x − 8
( x − 2 )( x 2 − 4 x + 4 )
=0
lim
=
x →2
x →2
( x − 2 )( x + 3 )
x2 + x − 6
→ La función no tiene asíntota vertical en x = 2.
lim
x 3 − 6 x 2 + 12 x − 8
= + ` → La función no tiene asíntota horizontal.
x → +`
x2 + x − 6

f ( x)
x 3 − 6 x 2 + 12 x − 8
=1
= lim
lim

3
2
x → +` x
x → +`
x + x − 6x


2
 x 3 − 6 x 2 + 12 x − 8


7
18
8
x
x
−
+
−

lim 
= −7
− x  = lim
2
2

x → + `
x + x −6
x + x −6
 x → + `

→ La función tiene una asíntota oblicua: y = x − 7.
lim
Si x = 1.000, f (x) − x + 7 > 0, y cuando x tiende a +` la función está
por encima de la asíntota.
Si x = −1.000, f (x) − x + 7 < 0, y cuando x tiende a −` la función
está por debajo de la asíntota.
c) Dom f = R − {2}
lim
x →2
0
x 3 − 6 x 2 + 12 x − 8
→
0
x −2
x 3 − 6 x 2 + 12 x − 8
( x − 2 )( x 2 − 4 x + 4 )
= 0 → La función
= lim
x →2
x →2
x −2
x −2
no tiene asíntota vertical en x = 2.
lim
lim
x → +`
lim
x → +`
x 3 − 6 x 2 + 12 x − 8
= + ` → La función no tiene asíntota horizontal.
x −2
f ( x)
x
oblicua.
408
= lim
x → +`
x 3 − 6 x 2 + 12 x − 8
= + ` → La función no tiene asíntota
x2 − 2x
SOLUCIONARIO
9
d) Dom f = R − {−2, 2}
x 3 − 6 x 2 + 12 x − 8
−64
→
2
x →−2
x −4
0

x 3 − 6 x 2 + 12 x − 8

=
−
lim −
`

x →−2
x2 − 4
 → La función tiene una asíntota vertical
3
2

x − 6 x + 12 x − 8
lim +
= + `
2
x →−2
x −4

lim
en x = −2. Por la izquierda la rama infinita de la función tiende a −`,
y por la derecha tiende a +`.
lim
x →2
x 3 − 6 x 2 + 12 x − 8
0
→
2
x −4
0
x 3 − 6 x 2 + 12 x − 8
( x − 2 )( x 2 − 4 x + 4 )
= 0 → La función
lim
=
x →2
x →2
( x − 2 ) ( x + 2)
x2 − 4
no tiene asíntota vertical en x = 2.
lim
lim
x → +`
x 3 − 6 x 2 + 12 x − 8
= + ` → La función no tiene asíntota horizontal.
x2 − 4

f ( x)
x 3 − 6 x 2 + 12 x − 8

1
= lim
=
x → +` x
x → +`

x 3 − 4x

2
 x 3 − 6 x 2 + 12 x − 8


−6x + 16x − 8

lim 
= −6
− x  = lim
2
2

 x → + `
x → + `
x −4
x −4

lim
→ La función tiene una asíntota oblicua: y = x − 6.
Si x = 1.000, f (x) − x + 6 > 0, y cuando x tiende a +` la función está
por encima de la asíntota.
Si x = −1.000, f (x) − x + 6 < 0, y cuando x tiende a −` la función
está por debajo de la asíntota.
e) Dom f = R − {2}
x 3 − 6 x 2 + 12 x − 8
0
lim
→
2
x →2
( x − 2)
0
( x − 2)3
x 3 − 6 x 2 + 12 x − 8
= 0 → La función no tiene asíntota
=
lim
x →2
x →2 ( x − 2 ) 2
( x − 2)2
vertical en x = 2.
lim
lim
x → +`
x 3 − 6 x 2 + 12 x − 8
= + ` → La función no tiene asíntota horizontal.
( x − 2)2

f ( x)
x 3 − 6 x 2 + 12 x − 8

=1
= lim
x → +` x
x → +`

x 3 − 4x 2 + 4x
 → La función
2

 x 3 − 6 x 2 + 12 x − 8

−2x + 8x − 8

 = lim
2
lim 
x
−
=
−

 x → + ` x 2 − 4x + 4
x → + `
x 2 − 4x + 4

lim
tiene una asíntota oblicua: y = x − 2.
f (x) − x + 2 = 0 → La expresión de la función coincide con la ecuación
de la asíntota salvo en x = 2.
409
Límite de una función
f ) Dom f = R → La función no tiene asíntota vertical.
x 3 − 6 x 2 + 12 x − 8
= + ` → La función no tiene asíntota horizontal.
x → +`
x2 + 4
f ( x)

x 3 − 6 x 2 + 12 x − 8
lim
= lim
=1

3
x → +` x
x → +`
x + 4x


2

 x 3 − 6 x 2 + 12 x − 8

+
−
6
x
8
x
8
−

lim 
− x  = lim
= −6
2
2
 x → + `
x → + `
x +4
x +4

→ La función tiene una asíntota oblicua: y = x − 6.
Si x = 1.000, f (x) − x + 6 > 0, y cuando x tiende a +` la función está
por encima de la asíntota.
Si x = −1.000, f (x) − x + 6 < 0, y cuando x tiende a −` la función
está por debajo de la asíntota.
lim
074
Calcula las ramas infinitas y asíntotas de las funciones.
a) y = x 2 + 5x − 1
b) y = 2 x − 1
c) y = log x
d) y = tg x
a) Dom f = R → La función no tiene asíntota vertical.
lim ( x 2 + 5x − 1) = + ` → La función no tiene asíntota horizontal.
x → +`
lim
x → +`
f ( x)
x
= lim
x → +`
x 2 + 5x − 1
= + ` → La función no tiene asíntota oblicua.
x
b) Dom f = R → La función no tiene asíntota vertical.
lim ( 2 x − 1) = + ` → La función no tiene asíntota horizontal.
x → +`
lim
x → +`
2x − 1
f ( x)
= lim
= + ` → La función no tiene asíntota oblicua.
x → +`
x
x
c) Dom f = (0, +`)
lim+ log x = − ` → La función tiene una asíntota vertical en x = 0.
x →0
La rama infinita de la función tiende a −`.
lim log x = + ` → La función no tiene asíntota horizontal.
x → +`
lim
x → +`
log x
f ( x)
= lim
= 0 → La función no tiene asíntota oblicua.
x → +`
x
x
 π

d) Dom f = R − + k π , k ∈ 
 2

1
lim tg x →
π
0
x→
2
lim− tg x = + `
π

2
 → La función tiene una asíntota vertical en x = π .
lim+ tg x = − ` 
2
π

x→
2

Por la izquierda la rama infinita de la función tiende a +`, y por la derecha, a −`.
Al ser una función periódica, de período π, todos los puntos
que no pertenecen al dominio son asíntotas del mismo tipo.
Por tanto, la función no tiene asíntotas horizontales ni oblicuas.
x→
410
9
SOLUCIONARIO
075
Encuentra las asíntotas de las funciones.
2 x − 3
a) y = 
x
 2 x − 3

 x
a) f ( x ) = 
 −2 x + 3

x

b) y =
2x
4 − x2
3
2
3
si x <
2
si x ≥
Dom f = R − {0}
−2 x + 3
3
lim
→
x →0
x
0

−2 x + 3
= − ` 
x →0

x
 → La función tiene una asíntota vertical en x = 0.

−2 x + 3
lim+
= + `
x →0
x

Por la izquierda la rama infinita de la función tiende a −`, y por la derecha, a +`.
lim−
2x − 3
= 2 → La función tiene una asíntota horizontal: y = 2.
x → +`
x
Si x = 1.000, f (x) < 2, y cuando x tiende a +` la función está por debajo
de la asíntota.
lim
−2x + 3
= −2 → La función tiene una asíntota horizontal: y = −2.
x → +`
x
Si x = −1.000, f (x) < −2, y cuando x tiende a −` la función está
por debajo de la asíntota.
Al tener asíntotas horizontales, la función no tiene asíntotas oblicuas.
lim
b) Dom f = (−2, 2)
2x
= −` → La función tiene una asíntota vertical en x = −2.
lim
+
x →−2
4 − x2
La rama infinita de la función tiende a −`.
2x
= + ` → La función tiene una asíntota vertical en x = 2.
lim
−
x →2
4 − x2
La rama infinita de la función tiende a +`.
Dado el dominio de la función, no tienen sentido los límites en el infinito,
y la función no tiene asíntotas horizontales ni oblicuas.
076
Observa la gráfica de la función
y determina estos límites.
lim− f ( x )
x →0
lim f ( x )
x →2−
lim+ f ( x )
x →0
lim f ( x )
x →3
Y
f (x)
lim f ( x )
x →0
lim f ( x )
1
x →2
1
X
Estudia la continuidad
de la función f (x).
411
Límite de una función
lim f ( x ) = 2
lim f ( x ) = 2
lim f ( x ) = 2
x →0+
x →0−
lim f ( x ) = 3
x →0
lim f ( x ) = 3,5
x →2−
lim f ( x ) = 3
x →3
x →2
La función es continua salvo en x = 2, ya que no existe f(2).
077
Completa la tabla para la función.
f (x) =
x2 − 2x − 3
x −3
Comprueba que su límite, cuando x tiende a 3, es: lim f ( x ) = 4
x →3
¿Cuánto vale f (3)? Haz una representación de la función.
¿Qué diferencia hay entre las gráficas de f (x) y de y = x + 1?
x
2,5
2,9
2,999
3,001
3,01
3,1
3,5
f(x)
3,5
3,9
3,999
4,001
4,01
4,1
4,5
No existe f(3).
Y
4
3
X
La gráfica de f(x) coincide con la gráfica de la recta y = x + 1,
salvo en el punto x = 3.
078
Dibuja una función que sea continua, salvo en x = −1, que tenga un salto infinito
y que tenga en x = 3 un salto finito.
Respuesta abierta.
Y
2
3
412
X
SOLUCIONARIO
079
9
Dibuja una función cuyo domino sea [0, + `), y que presente un punto
de discontinuidad evitable en x = 4.
Respuesta abierta.
Y
1
1
080
4
X
Determina los puntos de discontinuidad de las siguientes funciones.
x +2
x − 7x + 12
a) y =
1
x +3
e) y =
b) y =
x +2
x − x + 12
f) y =
x −5
2
2
c) y =
4+x
g) y =
x2 − 2x − 8
d) y =
4 − 3x − x 2
h) y =
x2 − 2x + 8
a) Dom f = R − {−3}
1
x
lim
→
x → −3 x + 3
0

1
= − ` 

x →−3 x + 3
 → No existe lim f ( x ) , y x = −3 es un punto

x →−3
1
lim +
= + `
de
discontinuidad
inevitable de salto infinito.

x →−3 x + 3

lim −
b) Dom f = R → No hay puntos de discontinuidad.
c) Dom f = [−4, +`) → No hay puntos de discontinuidad.
d) Dom f = [−4, 1] → No hay puntos de discontinuidad.
e) Dom f = R − {3, 4}
x+2
5
lim 2
→
x → 3 x − 7 x + 12
0

x +2
= + `

x → 3 x − 7 x + 12
 → No existe lim f ( x ), y x = 3 es un punto

x →3
x +2
lim+ 2
= − ` 
de
discontinuidad
inevitable de salto infinito.

x → 3 x − 7 x + 12

lim−
2
413
Límite de una función
lim
x→4
x+2
6
→
x − 7 x + 12
0
2

x+2
= − ` 

x → 4 x − 7 x + 12
 → No existe lim f ( x ) , y x = 4 es un punto

x→4
x+2
lim+ 2
= + `
de
discontinuidad
inevitable de salto infinito.

x → 4 x − 7 x + 12

lim−
2
f ) Dom f = [5, +`) → No hay puntos de discontinuidad.
g) Dom f = (−`, −2] ∪ [4, +`) → No hay puntos de discontinuidad.
h) Dom f = R → No hay puntos de discontinuidad.
081
Estudia la continuidad de las funciones en x = 3, y si presentan discontinuidad,
decide de qué tipo de discontinuidad se trata.
 x + 3

a) f ( x ) = 6
 2
 x − 2 x + 3
 12

x −1
b) f ( x ) = 
6
 x − 2

si x < 3
si x = 3
si x > 3
 12

(
)
=
f
x
d)
 x −3

 x − 15
si x < 3
 x + 1

e) f ( x ) =  x − 1

−2
si x = 3
si x > 3
 ln ( x − 2 )

c) f ( x ) =−2

 sen ( x − 3 )
si x < 3
si x ≥ 3
si x ≠ 3
si x = 3
si x < 3
si x = 3
si x > 3
a) f (3) = 6


 → lim f ( x ) = 6
2
x →3
lim+ f ( x ) = lim+ ( x − 2x + 3 ) = 6 
x →3
x →3

lim f ( x ) = lim− ( x + 3 ) = 6
x → 3−
x →3
Como f (3) = lim f ( x ), la función es continua en x = 3.
x →3
b) f (3) = 6

12
= 6 
x →3
x →3 x − 1
 → No existe lim f ( x ), y la función no es continua
lim+ f ( x ) = lim+ ( x − 2 ) = 1 en x = 3. x →3
x →3
x →3

Se trata de un punto de discontinuidad inevitable de salto finito.
lim− f ( x ) = lim−
c) f (3) = −2
lim f ( x ) = lim− (ln ( x − 2) ) = 0
x →3
 → lim f ( x ) = 0
x →3
lim+ f ( x ) = lim+ sen ( x − 3 ) = 0
x →3
x →3

x → 3−
Como f (3)
lim f ( x ), la función no es continua en x = 3.
x →3
Se trata de un punto de discontinuidad evitable.
414
SOLUCIONARIO
9
d) f (3) = −12
12

= − ` 
x →3
x →3 x − 3
 → No existe lim f ( x ), y la función no es
x →3
lim+ f ( x ) = lim+ ( x − 15) = −12
x →3
x →3
 continua en x = 3.
lim− f ( x ) = lim−
Se trata de un punto de discontinuidad inevitable de salto infinito.
e) f (3) = −2
lim f ( x ) = lim
x →3
x →3
Como f (3)
x +1
=2
x −1
lim f ( x ), la función no es continua en x = 3.
x →3
Se trata de un punto de discontinuidad evitable.
082
¿Qué valor debe tomar a para que las funciones sean continuas?
 3

a) f ( x ) =  x + 1
a

−2 x − 7
2 x −1
b) f ( x ) = 
ax − 2
 tg − π
c) f ( x ) = 
2x

log ( ax + 7 )
si x < −2
si x = −2
si x > −2
si x ≤ −2
si x > −2
si x ≤ −2
si x > −2
a) f (−2) = a

3

= −3
 → ∃ lim f ( x ) = −3
x →−2
x →−2 x + 1
x →−2

lim f ( x ) = lim + ( −2 x − 7 ) = −3 
x →−2
x →−2+

lim − f ( x ) = lim −
La función es continua si f (−2) = lim f ( x ) → a = −3.
x →−2
b) f ( −2) = 2−3 =
1
8

1

x →−2
x →−2
8

lim + f ( x ) = lim + ( ax − 2 ) = −2 a − 2 
x →−2
x →−2

lim − f ( x ) = lim − 2 x −1 =
→ ∃ lim f ( x ) si
x →−2
17
1
= −2 a − 2 → a = −
8
16
c) f (−2) = 1

−π

=1

x →−2
x →−2
2x
lim f ( x ) = lim + log ( ax + 7 ) = log ( −2a + 7 ) 
x →−2+
x →−2

lim − f ( x ) = lim − tg
→ ∃ lim f ( x ) si 1 = log ( −2a + 7 ) → a = −
x →−2
3
2
415
Límite de una función
083
Razona si la siguiente función es continua en x = 3 y en x = 0.
2 x − 1
y =  12

+3
 x
si x ≥ 3
si x < 3
f (3) = 7

12
+ 3 = 7 
 → ∃ lim f ( x )
x →3
x →3
x
x →3

x
lim f ( x ) = lim+ ( 2 − 1) = 7
x → 3+
x →3

lim− f ( x ) = lim−
Como f ( 3 ) = lim f ( x ), la función es continua en x = 3.
x →3
No existe f(0).

 12

lim− f ( x ) = lim− 
+ 3 = − ` 


x →0
x →0 
 x
 → No existe lim f ( x ), y la función no es continua

 12

x →0
lim+ f ( x ) = lim+ 
+ 3 = + `
en
x
=
0.

x →0
x →0 
 x

Se trata de un punto de discontinuidad inevitable de salto infinito.
084
Estudia la continuidad en todo el dominio de las funciones.
Determina los puntos de discontinuidad que presenta cada una de ellas.
a) y = sen (x + π)
b) y = ln (x + e)

π
c) y = tg  x − 

2
d) y = 2x−3
a) Dom f = R → No hay puntos de discontinuidad.
b) Dom f = (−e, +`) → No hay puntos de discontinuidad.
c) Dom f = R − {π + kπ, k ∈ }

lim− tg  x −

x →π

lim+ tg  x −

x →π

π 
 = + `

2
 → No existe lim f ( x ), la función no es continua
x →π

π 
 = − `  en x = π.
2

Se trata de un punto de discontinuidad inevitable de salto infinito.
Al ser una función periódica, de período π, todos los puntos en los que falla
el dominio son puntos de discontinuidad inevitable de salto infinito.
d) Dom f = R → No hay puntos de discontinuidad.
416
SOLUCIONARIO
085
9
Investiga si las funciones son continuas.
 log ( x + 7 )

a) f ( x ) =  1
 5

 x + 2
si x < 3
si x = 3
si x > 3
 3 x + 5

2
b) f ( x ) = 
 0

 x + 1
si x < −1
si x = −1
si x > −1
 5

2− x
c) f ( x ) = 
 5
 x +1
2 + 1
si x < 1
si x = 1
si x > 1
a) Si x < 3: f (x) = log (x + 7) → Dom f = (−7, 3) → No hay puntos
de discontinuidad.
Si x = 3: f (3) = 1
lim f ( x ) = lim− (log ( x + 7 )) = 1
x →3

 → ∃ lim f ( x ) = 1
5
x →3

lim+ f ( x ) = lim+
=1

x →3
x →3 x + 2
x → 3−
Como f ( 3 ) = lim f ( x ), la función es continua en x = 3.
x →3
5
→ Dom f = (3, +`) → No hay puntos
x+2
de discontinuidad.
Si x > 3: f ( x ) =
La función es continua en (−7, +`).
b) Si x < −1: f ( x ) =

 5
3x + 5
→ Dom f = − , − 1 → No hay puntos

 3
2
de discontinuidad.
Si x = −1: f (−1) = 1
 No existe lim f ( x ) , y la función no es
3x + 5
= 1
x →−1
x →−1
x →−1
2
 → continua en x = −1. Se trata de un punto

lim+ f ( x ) = lim+ ( x + 1) = 0  de discontinuidad inevitable de salto finito.

x →−1
x →−1
lim− f ( x ) = lim−
Si x > −1: f (x) = x + 1 → Dom f = (−1, +`) → No hay puntos
de discontinuidad.

 5
La función es continua en − , − 1 ∪ (−1, +`).

 3
417
Límite de una función
5
→ Dom f = (−`, 1) → No hay puntos de discontinuidad.
2− x
Si x = 1: f (1) = 5
5

lim− f ( x ) = lim−
= 5 
 → ∃ lim f ( x ) = 5
x →1
x →1 2 − x
x →1

lim+ f ( x ) = lim+ ( 2 x +1 + 1) = 5
x →1
x →1

c) Si x < 1: f ( x ) =
Como f ( 1) = lim f ( x ), la función es continua en x = 1.
x →1
Si x > 1: f (x) = 2 x + 1 + 1 → Dom f = (1, +`) → No hay puntos de discontinuidad.
La función es continua en R.
086
Estudia la continuidad de la siguiente función.
log ( t + 7 )


g(t ) =  2
 4

 7 − t
si t < 3
si t = 3
si t > 3
Si presenta puntos de discontinuidad, estudia el límite cuando t tiende a ellos
y decide qué tipos de discontinuidades son.
Si t < 3: g(x) = log (t + 7) → Dom f = (−7, 3) → No hay puntos de discontinuidad.
Si t = 3: g(3) = 2
lim g ( t ) = lim− log ( t + 7 ) = 1 
t →3

 → lim g ( t ) = 1
4
t →3

lim+ g ( t ) = lim+
=1

t →3
t →3 7 − t
t → 3−
Como g (3 ) = lim g( t ), la función es continua en t = 3.
t →3
Si t > 3: g ( t ) =
4
→ Dom f = (3, +`) − {7}
7−t

4
= + ` 

t →7
t →7 7 − t
 → No existe lim g( t ) y la función no es

t →7
4
lim+ g ( t ) = lim+
= − ` 
continua en t = 7.

t →7
t →7 7 − t
lim− g ( t ) = lim−
Se trata de un punto de discontinuidad inevitable de salto infinito.
La función es continua en (−7, 7) ∪ (7, +`).
087
Estudia la continuidad de las funciones.
a) y = [x]
b) y =
418
x
x
(Parte entera de x)
2
c) y = x − 1
d) y =
1
x − 1
2
SOLUCIONARIO
9
a) La función es continua salvo en los números enteros.
lim f ( x ) = a − 1

f ( x) .
Si a ∈ →
 → No existe xlim
→a
lim+ f ( x ) = a 
x →a

Todos los números enteros son puntos de discontinuidad inevitable de salto finito.
x → a−
−1 si x < 0
b) f ( x ) = 
1
si x > 0
No existe f (0).
lim f ( x ) = −1
x → 0−
 → No existe lim f ( x ), y la función no es continua en x = 0.
x →0
lim f ( x ) = 1 
x → 0+

Se trata de un punto de discontinuidad inevitable de salto finito.
La función es continua en R − {0}.
 x 2 − 1
si x < −1 o si x > 1
c) f ( x ) =  2
− x + 1 si −1 ≤ x ≤ 1
Si x = −1: f (−1) = 0
lim f ( x ) = lim− ( x 2 − 1) = 0 

x →−1
 → lim f ( x ) = 0
2
x →−1
lim+ f ( x ) = lim+ (− x + 1) = 0 
x →−1
x →−1

Como f (−1) = lim f ( x ) , la función es continua en x = −1.
x →−1−
x →−1
Si x = 1: f (1) = 0
lim f ( x ) = lim− ( −x 2 + 1) = 0 

x →1
 → lim f ( x ) = 0
2
x →1
lim+ f ( x ) = lim+ ( x − 1) = 0 

x →1
x →1
Como f (1) = lim f ( x ) , la función es continua en x = 1.
x →1−
x →1
La función es continua en R.
 1
 x 2 − 1
d) f ( x ) = 

1
 2
 −x − 1
No existe f (−1).
si x < −1 o si x > 1
si − 1 < x < 1

1
= + ` 
x →−1
x →−1 x − 1

 → La función no es continua en x = −1.

1
lim+ f ( x ) = lim+
= + `
2

x →−1
x →−1 − x + 1
Es un punto de discontinuidad inevitable de salto infinito.
No existe f (1).
1

lim− f ( x ) = lim−
= + `
2
x →1
x →1 − x + 1
 → La función no es continua en x = −1.


1
lim+ f ( x ) = lim+ 2
= + ` 

x →1 x − 1
x →1
Es un punto de discontinuidad inevitable de salto infinito.
La función es continua en R − {−1, 1}.
lim− f ( x ) = lim−
2
419
Límite de una función
088
Y
Observa la gráfica de la función
y determina los límites que se indican.
a) lim f ( x )
x →−`
1
b) lim f ( x )
f (x)
1
x →+`
c) lim f ( x )
x →−2
d) lim f ( x )
x →−1
a)
b)
089
lim f ( x ) = + `
c) lim f ( x ) no existe.
lim f ( x ) = 0
d) lim f ( x ) no existe.
x → −`
x →−2
x → +`
x →−1
Calcula los límites indicados en la función definida a trozos.
 x 2 + 5x + 1
h( x ) = 
3x 2 − 5x + 6
a) lim h( x )
x →−`
b)
lim h( x )
x →−1−
si x ≥ −1
lim h( x )
x →−1+
d) lim h( x )
x →+`
lim h ( x ) = lim ( x 2 + 5 x + 1) = + `
a)
x → −`
x → −`
lim f ( x ) = lim− ( x 2 + 5x + 1) = −3
b)
x →−1−
x →−1
lim h ( x ) = lim+ ( 3 x 2 − 5x + 6 ) = 14
c)
x →−1+
x →−1
lim h ( x ) = lim ( 3 x 2 − 5x + 6 ) = + `
d)
090
c)
si x < −1
x → +`
Calcula lim ( f
x →3
x → +`
g ), siendo las funciones:
g(x ) = x + 2
f (x) =
x2 −1
2 x 2 − 10x
x2 + 4x + 3
( x + 2 )2 − 1
=
2 x 2 − 2 x − 12
2 ( x + 2 )2 − 10 ( x + 2 )
x2 + 4x + 3
24
g ( x )) = lim 2
→
x → 3 2 x − 2 x − 12
0
g ( x ) = f ( g ( x )) = f ( x + 2 ) =
f
lim (f
x →3

x2 + 4x + 3

=
−
`
2

x → 3 2 x − 2 x − 12
 → No existe el límite.

x2 + 4x + 3
lim+
=
+

`
x → 3 2 x 2 − 2 x − 12

lim−
420
X
SOLUCIONARIO
091
9
Haz la gráfica aproximada de una función que cumpla las siguientes condiciones.
• lim f ( x ) = 0
x →−`
•
lim f ( x ) = + `
x →−2−
• lim f ( x ) = + `
x →+`
•
lim f ( x ) = − `
x →−2+
Respuesta abierta.
Y
1
1
092
X
Realiza la gráfica aproximada de una función que cumpla las siguientes condiciones.
• lim g ( x ) = −`
x →−`
• lim− g ( x ) = 3
x →2
• lim+ g ( x ) = −2
x →2
• lim g ( x ) = 0
x →+`
Respuesta abierta.
Y
2
2
X
421
Límite de una función
093
Construye la gráfica aproximada de una función que cumpla estas condiciones.
• lim h( x ) = 1
x →−`
• lim− h( x ) = − `
x →0
• lim+ h( x ) = + `
x →0
• lim h( x ) = 1
x →+`
Respuesta abierta.
Y
1
1
094
X
Representa tres funciones que cumplan que lim f ( x ) = 5 y cada una de estas
x →3
condiciones.
a) f(3) = 5
b) f(3) no existe.
c) f(3) = 2
Respuesta abierta.
a)
Y
5
3
422
X
SOLUCIONARIO
b)
9
Y
5
c)
3
X
3
X
Y
5
095
Dibuja una función continua que cumpla que f(x) es negativa si x > 3 y es positiva
si x < 3.
a) ¿Cuánto vale lim f ( x )? ¿Y f(3)?
x →3
b) ¿Hay un posible resultado? Razona la respuesta.
Respuesta abierta.
Y
1
3
X
a) lim f ( x ) = 0
x →3
f (3) = 0
b) Sí, porque si la función es continua tiene que verificarse que: lim f ( x ) = f (3)
x →3
423
Límite de una función
096
Halla las asíntotas de estas funciones.
f (x) =
x2 − 4x + 4
x 2 − x −2
g(x ) =
x 2 − 4x + 4
x 2 + x −2
Razona las diferencias entre ambas funciones.
Dom f = R − {−1, 2}
x2 − 4x + 4
9
→
x →−1 x 2 − x − 2
0
lim

x2 − 4x + 4

=
+
`

x →−1
x2 − x − 2
 → La función tiene una asíntota vertical en x = −1.
2

x − 4x + 4
lim+ 2
= − ` 
x →−1
x − x −2

lim−
lim
x →2
x2 − 4x + 4
0
→
2
x − x −2
0
x2 − 4x + 4
( x − 2 )2
lim
=
= 0 → La función no tiene una asíntota
x →2 x 2 − x − 2
x → 2 ( x − 1)( x − 2 )
vertical en x = 2.
lim
lim
x → +`
x2 − 4x + 4
= 1 → La función tiene una asíntota horizontal: y = 1.
x2 − x − 2
Al tener asíntotas horizontales, la función no tiene asíntotas oblicuas.
Dom g = R − {−2, 1}
lim
x →−2
x2 − 4x + 4
16
→
2
x + x −2
0

x2 − 4x + 4
= + `
2

x →−2
x + x −2
 → La función tiene una asíntota vertical en x = −2.
2

x −4x +4
lim + 2
= − ` 
x →−2
x + x −2

lim −
lim
x →1
x 2 − 4x + 4
1
→
2
x + x −2
0

x2 − 4x + 4

=
−
`

x →1
x2 + x − 2
 → La función tiene una asíntota vertical en x = 1.
2

x − 4x + 4
= + `
lim+ 2
x →1
x + x −2

lim−
lim
x → +`
x2 − 4x + 4
= 1 → La función tiene una asíntota horizontal: y = 1.
x2 + x − 2
Al tener asíntotas horizontales, la función no tiene asíntotas oblicuas.
Las funciones f(x) y g(x) tienen distintas asíntotas verticales, porque los valores
que anulan el denominador en cada una de ellas son diferentes.
424
SOLUCIONARIO
097
9
Escribe una función racional para cada caso.
a) Que tenga x = 2 y x = −3 como únicas asíntotas.
b) Sus únicas asíntotas son x = −2 e y = 3.
c) Sus asíntotas son x = 4 e y = 2x −1.
Respuesta abierta.
098
a) f ( x ) =
x4
( x − 2 )( x + 3 )
b) f ( x ) =
3x
x+2
c) f ( x ) =
2 x 2 − 9x
x−4
Calcula el valor de a para que el límite tenga valor finito: lim
x →+`
Con ese valor de a, halla b para que se verifique que:
lim
x →+ `
2x2 + 3
− ax .
x −1
2x2 + 3
− ax − b = 0
x −1
¿Qué relación existe entre la función y =
2x2 + 3
y la recta y = ax + b?
x −1

 2x 2 + 3
2 x 2 + 3 − ax 2 + ax
− ax  = lim
lim 
 x → + `
x → +` 
x −1
x −1
El límite tiene valor finito si el grado del numerador es menor o igual
que el denominador, por lo que a = 2.

 2x 2 + 3
3 + 2 x − bx + 1
= 2−b = 0 → b = 2
lim 
− 2 x − b = lim
 x → + `
x → +` 
x −1
x −1
La recta y = 2x + 2 es la asíntota oblicua de la función y =
099
2x 2 + 3
.
x −1
Se ha estimado que la población de zorros en una finca se rige
6t 2 + 3
por la fórmula z = 100
, donde z representa el número de zorros
2 + t2
y t es el tiempo transcurrido, en meses.
El veterinario de la finca ha observado que, en los primeros seis meses, la población
ha aumentado. Investiga si el crecimiento será indefinido, si tenderá a estabilizarse
la población o si tenderá a disminuir.

6 t 2 + 3 
 = 600
lim 100 ⋅
t → + `
2 + t 2 
La población de zorros tenderá a estabilizarse.
425
Límite de una función
100
mc
La famosa fórmula M =
se debe a Einstein, y expresa la masa M de un
c2 − v2
cuerpo en función de su velocidad v, siendo c la velocidad de la luz (300.000 km/s).
Calcula el límite de la masa M cuando v tiende a c. A la vista de ese resultado,
¿crees que un cuerpo puede alcanzar esa velocidad?
lim
v →c
mc
c2 − v 2
= +`
Para que la velocidad llegara a ser la de la luz el cuerpo debería tener
una masa infinita.
101
Representa mediante una función definida a trozos la tarifa de un aparcamiento.
APARCAMIENTO
Horario: de 10:00 a 22:00 horas
Tarifas:
• Cada hora o fracción: 2 €
• Más de 5 horas: 10 €
• Estancia máxima: 12 horas
a) Estudia su continuidad.
b) Clasifica los puntos de discontinuidad, si los tuviera.
Y
10
8
6
4
2
2
4
6
8
X
a) La función no es continua en:
x = 10
x = 11
x = 12
x = 13
x = 14
b) Los puntos son de discontinuidad inevitable de salto finito.
426
SOLUCIONARIO
9
PARA FINALIZAR…
102
Calcula el valor de k para que el siguiente límite sea un número real: lim
x →2
x 2 + kx + 2
x2 − 4
Para el valor de k obtenido, ¿cuánto vale el límite?
lim
x →2
x 2 + kx + 2
2k + 6
→
2
x −4
0
Si k = −3, entonces la indeterminación es:
Así, el límite vale: lim
x →2
103
0
0
( x − 2 )( x − 1)
x 2 − 3x + 2
1
=
= lim
2
x → 2 ( x − 2 )( x + 2 )
x −4
4
Calcula los límites.
a) lim x ⋅ sen
x →0
1
x
b) lim
x →`
1
⋅ cos x
x
Aunque no sepamos el valor que toman el seno y el coseno de un ángulo cuando
el ángulo tiende a infinito, sí sabemos que es una cantidad acotada,
pues tanto el seno como el coseno de un ángulo tienen un valor comprendido
en [−1, 1], y al multiplicar por cero una cantidad acotada, el resultado es cero.
a) lim x ⋅ sen
x →0
104
1
=0
x
b)
lim
x→ +`
1
⋅ cos x = 0
x
¿Qué ocurrirá con las raíces de la ecuación ax 2 + bx + c = 0 si el coeficiente a tiende
a cero y los coeficientes b y c son constantes, siendo b 0?
Las soluciones de la ecuación son de la forma: x =
lim
a→0
lim
−b + b 2 − 4 ac
0
→
2a
0
− b + b 2 − 4 ac
a→0
= lim
lim
a→0
−b ± b 2 − 4 ac
2a
−b − b 2 − 4 ac
−2 b
→
→`
2a
0
b 2 − ( b 2 − 4 ac )
=
2a(− b − b 2 − 4 ac )
c
2c
= lim
=−
a→0
b
− b − b 2 − 4 ac
a→0
2a
1
105
Comprueba que lim e x no existe.
x →0
1

1

 → No exiiste lim e x .
x →0

= + `

lim− e x = 0
x →0
1
lim+ e x
x →0
427
Límite de una función
106
Estudia la continuidad de cada una de las siguientes funciones.
2 x
a) y =  1
5 x

si x ≤ 0
 x1
b) y = 5
2 x

si x > 0
si x < 0
si x ≥ 0
 x 2 ⋅ sen 1 si x 0
c) y = 
x

si x = 0
0
a) f (0) = 1



1
x
lim 5 = + `
x → 0+

lim 2 x = 1
x → 0−
No existe lim f ( x ), y la función no es continua en x = 0.
x →0
Se trata de un punto de discontinuidad inevitable de salto infinito.
La función es continua en R − {0}.
b) f (0) = 1
1

lim− 5 x = 0
x →0

lim+ 2 x = 1 
x →0

No existe lim f ( x ), y la función no es continua en x = 0.
x →0
Se trata de un punto de discontinuidad inevitable de salto finito.
La función es continua en R − {0}.
c) f (0) = 0

1
lim  x 2 ⋅ sen  = 0

x →0 
x 
Al ser f (0 ) = lim f ( x ) , la función es continua en x = 0.
x →0
Así, la función es continua en R.
107
Demuestra que la recta de ecuación y =
de la hipérbola
y2
x2
−
= 1.
a2
b2
b
x es una asíntota
a
y2
b2 x 2 − a2 b2
x2
2 2
2 2
2 2
2
−
=
1
→
−
=
→
=
b
x
a
y
a
b
y
a2
a2
b2
→ y =±
428
b
lim 
x → +` 
a
x 2 − a2 −
b
a
b
lim 
x →+ ` 
a
x 2 − a2 −
b
b 
x  = lim  ⋅
a  x →+ `  a
b2 x 2 − a2 b2
b
=±
2
a
a

x  → ` − `


 = 0

x 2 − a 2 + x 
− a2
x 2 − a2
9
SOLUCIONARIO
108
Si medimos el ángulo x en radianes, demuestra que lim
sen x
x →0
x
Si el ángulo x se mide en grados sexagesimales, entonces lim
= 1.
sen x
x →0
Como la medida de la longitud del arco está comprendida
entre la longitud de los segmentos AC y AB, entonces
el área del sector circular está comprendida entre el área
de los triángulos.
Área de OAC < Área de sector < Área OAB
R ⋅ R sen x
2
R 2 sen x
2
< πR2 ⋅
< R2 ⋅
x
=
π
.
180
C
x
O
B
A
R ⋅ R tg x
x
<
2π
2
R 2 tg x
x
<
2
2
Simplificamos dividiendo entre
Dividimos entre sen x:
sen x
sen x
→
<
sen x
sen x
R2
: sen x < x < tg x
2
tg x
x
<
sen x
sen x
>
sen x
x
>
sen x
→ 1>
sen x
> 1 → lim
sen x
tg x
x
> cos x
Hacemos límites con x → 0:
lim 1 > lim
x →0
x →0
sen x
> lim cos x → 1 > lim
x →0
sen x
x →0
x
que queríamos demostrar.
x
x →0
x
= 1, que es lo
Si x viene medido en grados:
R ⋅ R sen x
2
< πR 2 ⋅
R ⋅ R tg x
R 2 sen x
R 2 tg x
x
πR 2
<
<
⋅x<
→
360
2
2
360
2
Simplificamos dividiendo entre
R2
π
⋅ x < tg x
: sen x <
2
180
Dividimos entre sen x:
sen x
tg x
π
π
1
x
x
<
⋅
<
→ 1<
⋅
<
180 sen x
180 sen x
sen x
sen x
cos x
180 sen x
→ 1>
⋅
> cos x
x
π
Hacemos límites con x → 0:
lim 1 > lim
x →0
x →0
sen x
180 sen x
180
>1
⋅
> lim cos x → 1 >
⋅ lim
x →0
x
π
π x →0 x
sen x
180
→
⋅ lim
=1
π x →0 x
Y despejando, resulta que: lim
x →0
sen x
x
=
π
180
429