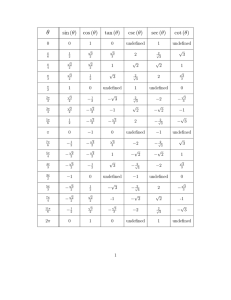
3. r2 = 9 sin 2θ, r ≥ 0,0 ≤ θ ≤ π

3. r2 = 9 sin 2θ, r ≥ 0, 0 ≤ θ ≤ π/2
∫ π
2 1
· 9 sin 2θdθ
Area =
0 2
π
2
9
= − cos 2θ
4
0
9
=
2
4. r = tan θ, π/6 ≤ θ ≤ π/3
∫ π
3 1
Area =
tan2 θdθ
π
2
6∫ π
1 3
=
sec2 θ − 1dθ
2 π6
1 √
1
π π
=
( 3− √ − + )
2
6
3 3
1√
1
3− π
=
3
12
11. r = 3 + 2 cos θ
∫
1 π
Area = 2 ·
(3 + 2 cos θ)2 dθ
2
0
∫ π
=
9 + 12 cos θ + 4 cos2 θdθ
0
= 11π
23.
∫
π
3
Area =
∫
− π3
π
3
=
1
[(2 cos θ)2 − 1]dθ
2
4 cos2 θ − 1dθ
0
√
π
3 2
=
+ π−
2
3
3
√
3 1
=
+ π
2
3
27.
∫
π
3
Area =
∫
− π3
π
3
=
1
[(3 cos θ)2 − (1 + cos θ)2 ]dθ
2
8 cos2 θ − 2 cos θ − 1dθ
0
= π
1
31.
∫
π
8
1
Area = 16
(sin 2θ)2 dθ
2
0
∫ π
8
4 sin2 θ cos2 θdθ
= 8
∫0 π
8
= 32
cos2 θ − cos4 θdθ
∫0 π
8 1
1
= 32
− cos2 2θdθ
4 4
π 0
=
−1
2
33.
∫
π
8
1
sin 2θdθ
0 2 π
= − cos 2θ|08
√
2
= 1−
2
Area = 4
38.
1 − cos θ = 1 + sin θ
⇒
tan θ = −1
3 7
⇒
θ = π, π
4 4
Figure 1: Ex. 38
2
46. r = 5θ , 0 ≤ θ ≤ 2π
∫ 2π √
dr
L =
r2 + ( )2 dθ
dθ
∫0 2π √
52θ + (5θ ln 5)2 dθ
=
0
∫ 2π √
=
5θ 1 + (ln 5)2 dθ
0
θ 2π
√
5
=
1 + (ln 5)2 ·
ln
5
0
√
1 + (ln 5)2 2π
=
[5 − 1]
ln 5
47. r = θ2 , 0 ≤ θ ≤ 2π
∫ 2π √
L =
θ4 + 4θ2 dθ
0
∫ 2π √
=
θ 4 + θ2 dθ
0
1
3 2π
=
(4 + θ2 ) 2 3
0
8
3
((1 + π 2 ) 2 − 1)
=
3
48. r = 2(1 + cos θ)
∫
L = 2
π
√
4(1 + cos θ)2 + 4 sin2 θdθ
∫0 π √
= 4
2(1 + cos θ)dθ
0
π
θ = 16 sin 2 0
= 16
55.
(a) Let x = r cos θ, y = r sin θ
√
∫ β
dx
dy
(10.2.6)
S =
2πy ( )2 + ( )2 dt
dt
dt
√
∫αb
d
d
=
2πr sin θ ( r cos θ)2 + ( r sin θ)2 dθ
dθ
√ dθ
∫a b
dr
=
2πr sin θ r2 + ( )2 dθ
dθ
a
3
(b) r2 = cos 2θ
∫
√
π
4
sin2 2θ
2
2πr sin θ cos 2θ +
dθ
cos 2θ
0
√
∫ π√
4
1
4π
cos 2θ sin θ
cos 2θ
0
∫ π
4
4π
sin θdθ
0
√
2π(2 − 2)
S =
=
=
=
56.
(a)
∫
S=
√
b
2πr cos θ
dr 2
) dθ
dθ
r2 + (
a
(b)
∫
√
π
4
S = 2
2πr cos θ
0
sin2 2θ
cos 2θ +
dθ
cos 2θ
π
sin θ|04
= 4π
√
= 2 2π
4