La segunda ley de Newton: F=ma. Colisiones elásticas. (carril de

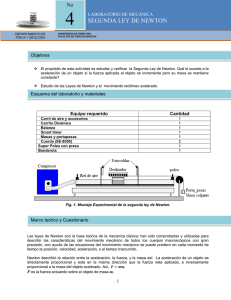
Guía del experimento
Física Básica Experimental
La segunda ley de Newton: F=ma.
Colisiones elásticas.
(carril de aire)
Departamento de Física Aplicada.
Universidad de Cantabria
Resumen
Se utiliza un dispositivo mediante el cual se ha reducido apreciablemente
el rozamiento. En la primera parte, se pone de manifiesto la
proporcionalidad entre la fuerza aplicada a un objeto y la aceleración que
éste adquiere. Se aplican fuerzas constantes que provocan movimientos
uniformemente acelerados. En la segunda parte, se estudian las leyes de
conservación en una colisión elástica producida en una dimensión.
Introducción teórica I: La segunda ley de Newton.
¿Qué mecanismo hace que se produzca una variación en el movimiento de los
objetos? ¿Por qué unos objetos se aceleran más que otros? Los conceptos de fuerza y
masa permiten contestar estas preguntas. Aparecen en las leyes fundamentales del
movimiento formuladas por Sir Isaac Newton hace ya tres siglos. Estas leyes se basan en
la observación experimental. Con ayuda de la bibliografía, enuncie las tres leyes de
Newton del movimiento.
La segunda ley de Newton F1 = m a representa la ecuación diferencial del
movimiento de una partícula de masa m y tiene carácter vectorial. A partir de esta
ecuación, con las condiciones iniciales r(t=0)=r0 y v(t=0)=v0 y considerando a
=constante, obtenga la velocidad y la posición de la partícula en cualquier tiempo t.
Particularice el resultado a un movimiento unidimensional, según el eje x, por ejemplo.
Haga una representación gráfica de la solución obtenida para la velocidad y la posición
de la partícula en función del tiempo.
Reflexiones previas a la realización del experimento.
Antes de llevar a cabo las experiencias considere las siguientes cuestiones:
1.- ¿Es fácil observar la primera ley de Newton? ¿por qué? ¿cuál es la utilidad de un
carril de aire?
2.- ¿Es posible que exista movimiento en ausencia de fuerza? ¿y fuerza en ausencia de
movimiento? Si una sola fuerza actúa sobre un objeto ¿se acelerará el objeto?
3.- ¿Si un objeto está acelerado, ¿está actuando una fuerza soble él? Si un objeto no está
acelerado, ¿ es porque no actúa ninguna fuerza sobre él?
4.- ¿Si un objeto experimenta una fuerza neta en la dirección x, ¿se mueve en la
dirección x?
5.- Un tren esta formado por una locomotora que arrastra un conjunto de vagones,
unidos, cada uno al siguiente, por un enganche. El tren acelera en el sentido de la
marcha. Al ir desde la locomotora hacia el vagón de cola, la fuerza ejercida por los
enganches ¿aumenta , disminuye o se mantiene? ¿y si el tren decelera?
1
Se expresan en negrita las magnitudes con carácter vectorial.
1
Guía del experimento
Física Básica Experimental
Descripción del material
Para llevar a cabo este experimento se utiliza el siguiente material:
Carril de aire
Dispositivo de arranque
Deslizador y accesorios
Polea de precisión
Pesas
Hilo
Tope
Contador de tiempos 4x4
Cuatro barreras de luz
Cuatro soportes (base+barra)
Cuatro nueces dobles
Cables de conexión (amarillo,rojo,azul)
Modo operativo
Figura 1.- Montaje experimental para estudiar la proporcionalidad entre la fuerza que se
aplica a un objeto y la aceleración que dicho objeto experimenta.
Con ayuda del profesor debe montar el dispositivo de la figura 1. El profesor le
explicará como utilizar el dispositivo de arranque y cómo utilizar el contador de tiempos
(CT).
Se trata de medir cuatro pares de valores (xi , ti) de la trayectoria que describe el
deslizador para reconstruir la posición como función del tiempo y obtener las funciones
velocidad y aceleración. La masa del deslizador, md, es susceptible de ser modificada
colocando pesas en los laterales del mismo, asegurándose de hacerlo de forma simétrica
para que el rozamiento sea mínimo. Observe el dispositivo experimental que permite
aplicar al deslizador una fuerza constante. Dicha fuerza constante también puede ser
modificada cambiando la masa mF (el número de pesas) que se colocan al final del hilo
de seda.
Fije la fuerza que va a aplicar al deslizador. Fije la masa del deslizador.
Coloque las barreas de luz a intervalos ∆x iguales para facilitar los cálculos
posteriores. Coloque el tope elástico, que se observa en la figura 1, de tal manera que las
pesas de aceleración no lleguen a tocar el suelo.
Determine los valores ti con el CT en modo “s(t)” (consulte al profesor). Repita las
medidas el número adecuado de veces. Tabule los resultados. Determine la aceleración a
del deslizador. ¿Cómo lo hará? Represente gráficamente los resultados.
Determine a continuación las velocidades vi utilizando el CT en modo “v(t)”
(consultar al profesor). ¿Qué velocidad es la que calcula exactamente con este montaje
experimental? ¿Hace alguna aproximación? ¿Podría evaluarla? Tabule los resultados.
2
Guía del experimento
Física Básica Experimental
Determine la aceleración a del deslizador. ¿Cómo lo hará? Represente gráficamente los
resultados.
Escriba la segunda ley de Newton aplicada al “sistema” que le permite obtener la
aceleración de md. Obtenga a y compare el resultado con los que ha obtenido
previamente.
Modifique la masa del deslizador md (auméntela 20g cada vez) y repita las medidas
anteriores.
Represente gráficamente la fuerza aplicada en función de la aceleración producida.
Extraiga sus conclusiones. En todo caso, calcule errores de medida.
Introducción teórica II: Colisiones elásticas.
Reflexiones previas a la realización del experimento
1.- Encuentre en bibliografía las definiciones de impulso de una fuerza y cantidad de
movimiento de una partícula.
2.- ¿Cómo se define una colisión? ¿Qué modelo se utiliza para estudiar las colisiones?
¿Qué aproximaciones se hacen?
3.- ¿Qué magnitudes físicas se conservan en una colisión elástica entre dos objetos?
Escriba las correspondientes ecuaciones en una dimensión.
Modo operativo
Con ayuda del profesor debe montar el dispositivo de la figura 2. El profesor le
explicará como utilizar el dispositivo de arranque y cómo utilizar el contador de tiempos
(CT).
Figura 2.- Montaje experimental para estudiar las colisiones elásticas.
Se provoca una colisión entre dos deslizadores, en las siguientes condiciones: Un
deslizador de masa m1, cuya velocidad antes del choque es v1, colisiona con otro
deslizador de masa m2, que se mantiene en reposo. Utilizando el CT en modo “v(t)”, se
miden v1 y las velocidades después del choque, v1’ y v2’. ¿Qué es lo que mide
exactamente con este montaje experimental? ¿Ocurre lo mismo que en el experimento
anterior? Repita las medidas un número adecuado de veces y tabule los resultados. El
3
Guía del experimento
Física Básica Experimental
dispositivo de arranque le permite comunicar, muy aproximadamente, el mismo impulso
inicial a m1. Represente en la misma gráfica el momento lineal de los sistemas m1, m2 y
m1 + m2 antes y después de la colisión. Haga lo mismo con la energía cinética. Extraiga
sus conclusiones. Modifique la masa m2 y repita el experimento. En todo caso, calcule
errores de medida.
Otros posibles experimentos:
1.- Colisión de un deslizador con una cinta elástica.
2.- Colisión inelástica de dos deslizadores
Preguntas adicionales relacionadas con la experiencia
Este experimento ha sido realizado en el sistema laboratorio. Defina el sistema centro
de masas (CM) y haga lo siguiente:
A) Calcule la velocidad del CM de los dos deslizadores antes del choque. Considere un
sistema de referencia con origen en el CM y que se mueve con él. B) ¿Es inercial este
marco de referencia? C) ¿Qué velocidades iniciales u1 y u2 tienen los dos deslizadores
en este sistema CM? D) ¿cuánto vale la cantidad de movimiento total en el sistema CM?
E) Utilice la conservación de la cantidad de movimiento y de la energía, aplicadas en el
sistema CM, para relacionar la cantidad de movimiento final de cada deslizador con la
inicial (y la velocidad final de cada deslizador con la inicial). El resultado debe mostrar
que un choque elástico unidimensional tiene una descripción sencilla en el sistema CM,
¿por qué? ¿qué es lo que ocurre? Calcule las velocidades u1 y u2, aplique el resultado de
la parte E) y obtenga las velocidades finales u1’ y u2’ en el sistema CM y luego
transfórmelas para obtener las velocidades finales, v1’ y v2’, en el sistema laboratorio.
Referencias
[1] P. A. Tipler. Física. Ed. Reverté. 4ª edición (1999).
[2] Sears, Zemansky, Young, Freeman, Física Universitaria. Addison-Wesley.11ª
edición (2004).
[3] R. A. Serway y J. W. Jewett Física. Mc. 3ª ed. Ed. Thomson (2003).
4