Tema 1. Iteraciones. Ceros de una función como puntos fijos

Tema 1. Iteraciones.
Ceros de una función como puntos fijos atractores de otra.
El método de Newton y alternativas a él.
Referencia: [San98], Cap. 9.1
1. Ejemplo 1. Hallar raı́ces cuadradas:
x2 = a2 + b
√
Si por ejemplo queremos x = 19 , podemos escribir
x = a + b/(x + a)
⇒
x2 = 42 + 3 , luego x = 4 + 3/(x + 4)
De la aproximación x ≈ 4 sale otra mejor: x ≈ 4 + 3/8 = 35/8 , y de esa otra mejor . . .
La idea aparece ya en la antigua Babilonia. En lenguaje moderno se puede explicar ası́:
√
La función g(x) = a + b/(x + a) fija el punto c = a2 + b > 0 , y las imágenes iteradas
xk = g(xk−1 ) de cualquier x0 > 0 convergen a c .
Decimos entonces que c es un punto fijo atractor de g .
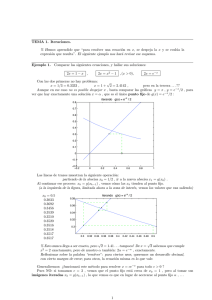
El gráfico de la izquierda corresponde al caso c2 = 2 = 12 + 1 , x0 = 1 , y muestra cómo se producen
las iteradas xk = 3/2, 7/5, . . . con g(x) = x = 1 + 1/(x + 1) .
! 1.1
2
2
1.8
1.8
1.6
1.6
1.4
1.4
1.2
1.2
1
1
0.8
0.8
0.6
0.6
0.4
0.4
0.2
0
0
0.2
0.5
1
1.5
2
0
0
0.5
Pero el mismo c cumple c2 = 2 = 22 − 2 , luego c = 2 − 2/(c + 2) .
¿Funciona también esta g? ¿Cuál es mejor? . . .
1
1.5
2
Ver gráfico de la derecha.
2. PROPOSICION : Si |g " | < 1 cerca de c = g(c) , c es un punto fijo atractor de g ; si g aplica
en sı́ mismo un intervalo cerrado J en el que |g " | < 1 , hay en J un único punto fijo, y es atractor.
Prueba:
Si c está en algún intervalo J en el que |g " | < α < 1 , el TVM , junto con c = g(c) , implica que
c − g(x) = (c − x)g " (ξ) para algún ξ entre ambos, luego |c − g(x)| < α|c − x| , y los c − xk → 0
más rápido que αk . Si g aplica J = [a, b] en sı́ mismo, la función continua g(x) − x cambia de
signo en J , luego se anula en algún c ∈ [a, b] , y no pueden ser en dos de ellos, porque serı́a
c1 − c2 = g(c1 ) − g(c2 ) = g " (ξ)(c1 − c2 ) , contradicción.
. . . en el Ejemplo 1:
Para g(x) = a + b/(x + a) es g " (c) = −b/(c + a)2 = (a − c)/(a + c) , que tiene | | < 1 si ac > 0 ,
luego c es atractor para g . Si b > 0 , es g " (c) < 0 , con lo que c está entre cada dos xk sucesivos.
! 1.2
1 Otra
lectura recomendada: Hubbard/ West. Differential Equations, Chap.5.
1
Ejemplo 2. Posibles iteradores g(x) para aproximar la solución de x3 − x = 1 :
!
g1 (x) = x3 − 1 , g2 (x) = 1 + 1/x , g3 (x) = x − k(x3 − x − 1) , para alguna k adecuada.
El punto c buscado, donde se anula F (x) = x3 − x − 1 , no es atractor de g1 , pero sı́ de g2 . Es fácil
ver que F " (c) ∈ (2, 6), lo que sugiere k = 1/4 , es decir g3 (x) = x − (x3 − x − 1)/4 ; tras aproximar
c , podemos ver que g3" (c) = 0.066 , lo que dio una convergencia bastante rápida, hubo suerte.
Además los iterados xk = g3 (xk−1 ) van hacia c = 1.3247 , no importa el x0 . Por el contrario, . . .
Ejemplo 3. Sea c el cero de F (x) = x3 − 3 . Como F " (c) = 3c2 ≈ 6 , podemos tomar
g(x) = x − F (x)/6 .
La convergencia es muy buena, si no empezamos demasiado lejos !!
! 1.3
DEFINICION: La cuenca de un atractor c es el {x0 tales que las xk = g(xk−1 ) → c}.
3. La idea que generaliza los Ejemplos anteriores:
Si F (c) = 0 , cada
g(x) = x − k(x)F (x)
fija c , y c es atractor si |1 − k(c)F " (c)| < 1 .
Lo ideal es g " (c) = 0 , como intenta conseguir el método de Newton:
g(x) = x − F (x)/F " (x)
g(x) = la abscisa donde corta al eje x la recta tangente en (x, F (x)) a la gráfica de F .


 (x + a/x)/2
 x2 − a
2
2
Ejemplos de Newton : g(x) = 2x/3 + 1/x
si F (x) = x3 − 3 (el Ejemplo 3)


x(2 − ax)
a − 1/x
Convergencia de Newton en un cero simple, y qué hacer en uno múltiple:
En un cero simple de F , Taylor nos da F (c + ξ) = aξ + O(ξ 2 ) con a '= 0 , luego
la g(x) = x − F (x)/F " (x) cumple g(c + ξ) = c + O(ξ 2 ) , convergencia cuadrática !
Pero en un cero de orden k , es F (c + ξ) = aξ k + O(ξ k+1 ) , F " (c + ξ) = kaξ k−1 + O(ξ k ), y hay que
tomar g(x) = x − k F (x)/F " (x) para lograr lo mismo.
! 1.4
4. Versión “más barata” de Newton: secantes en vez de tangentes.
Si ya tenemos dos puntos (xi , fi ) , i = 0, 1 de la gráfica de f , alinear con ellos un nuevo punto
(x2 , 0) significa que se tenga
x2 − x0
0 − f0
=
x1 − x0
f1 − f0
y si llamamos ∆x0 = x1 − x0 , ∆f0 = f1 − f0 , resulta
x2 = x0 − f0 / (∆f0 /∆x0 )
.
Nótese la similitud con el método de Newton: f " se ha reemplazado por un cociente de incrementos.
La convergencia es menos rápida: puede probarse que si F " (c) '= 0 , se tiene xn+1 −c = O(|xn −c|φ ),
con φ = 1.62 (la razón áurea); pero la diferencia entre ese exponente y 2 es casi irrelevante: sólo
multiplica por el factor 2/φ el número de pasos hasta alcanzar cierta precisión.
A cambio, el método es ventajoso cuando la derivada es complicada o “inasequible”, porque los
datos fi son producidos por un proceso y no por una fórmula que podamos derivar.
! 1.5
2 El
último es el algoritmo “multiplicar para dividir”, que aproxima 1/a sin hacer divisiones.
2
5. Ideas adicionales3 .
• Extrapolación (Aitken’s ∆2 ).
Si 1 > |g " (c)| =
' 0 , los xk = g(xk−1 ) tienden casi geométricamente a c , con razón r = g " (c) ;
pero eso permite estimar r , y la posición del lı́mite c : con la misma notación ∆ usada antes, y
escribiendo igualdades (aunque sólo son aproximadas),
r=
∆x1
∆x0
,
c − x0 = ∆x0 (1 + r + r2 + . . .) =
∆x0
(∆x0 )2
=− 2
1−r
∆ x0
donde hemos llamado ∆2 x0 = ∆x1 − ∆x0 .
Podemos por ejemplo tomar esa estimación de c como siguiente abscisa inicial:
nuevo x0 := x0 − (∆x0 )2 /∆2 x0
.
! 1.6
• A veces se puede hacer mejor: escoger k(x) para anular más derivadas de g en c .
• El nivel global: estudiar
x/2 = sen(x)
! 1.7
como ejemplo de la estructura fractal de las cuencas.
Se verá este Ejemplo en B1. Ver también Problema 9.5.2 de [San98].
• Cómo extender todo esto a dim > 1 .
Para aproximar ceros de una F : IRn → IRn , es igualmente posible buscar funciones g que los
tengan por puntos fijos, y es la matriz derivada Dg(c) quien controla la convergencia.
El método de Newton usa la A(x) = DF (x) para producir:
En el Tema 2 se usará un caso “sencillo” de esta idea.
3 Sólo
para quienes hayan entendido bien lo anterior !!
3
g(x) = x − A(x)−1 F (x)
.
! 1.8