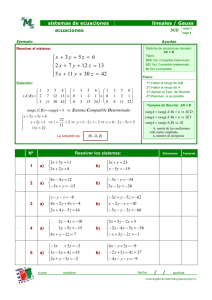
Solución única Solución única Infinitas soluciones Sin solución Sin

TEMA 3: RESOLUCIÓN DE SISTEMAS DE ECUACIONES MEDIANTE DETERMINANTES.
2º BACH(CN)
TEMA 3: RESOLUCIÓN DE SISTEMAS DE ECUACIONES MEDIANTE DETERMINANTES.
1.-INTRODUCCIÓN.
La resolución de sistemas de ecuaciones está ligada al estudio de la posición relativa de
rectas o planos.
Cuando resolvemos un sistema de ecuaciones con dos incógnitas estamos estudiando la
posición relativa de las rectas que forman el sistema de ecuaciones:
Solución única
Solución única
Infinitas soluciones
Sin solución
Sin solución
DAVID RIVIER SANZ
3-1
TEMA 3: RESOLUCIÓN DE SISTEMAS DE ECUACIONES MEDIANTE DETERMINANTES.
2º BACH(CN)
Y cuando resolvemos un sistema de ecuaciones con tres incógnitas estudiamos la
posición relativa de los planos que forman el sistema:
Solución única
Solución única
Sin solución
Infinitas soluciones
Sin solución
Dependiendo de esas posiciones relativas diremos si tienen solución o no los sistemas,
así tendremos:
Una solución
Con solución
COMPATIBLE
SISTEMA
Infinitas
Soluciones
DETERMINADO
INDETERMINADO
Sin solución
INCOMPATIBLE
DAVID RIVIER SANZ
3-2
TEMA 3: RESOLUCIÓN DE SISTEMAS DE ECUACIONES MEDIANTE DETERMINANTES.
2º BACH(CN)
2.-DISCUSIÓN DE SISTEMAS DE ECUACIONES.
Discutir un sistema de ecuaciones dependiente de uno o más parámetros consiste en
identificar el sistema es compatible, distinguiendo los casos en los que es determinado o
indeterminado, o incompatible. Si lo hacemos utilizando el Método de Gauss para resolver
sistemas que vimos el curso pasado, al finalizar el proceso podíamos llegar a uno de las
siguientes situaciones:
(I)
donde
y
e
cualquier número,
entonces el sistema es COMPATIBLE DETERMINADO.
(II)
donde
y
e
cualquier número,
entonces tenemos menos ecuaciones válidas que incógnitas, entonces el sistema es
COMPATIBLE INDETERMINADO.
(II)
donde
y
e
cualquier número, entonces la
última ecuación del sistema no se puede cumplir nunca, entonces el sistema es
INCOMPATIBLE.
3.-TEOREMA DE ROUCHÉ.
Definición.- Dado un sistema de ecuaciones de n incógnitas y n ecuaciones:
(*)
llamamos matriz de coeficientes a la matriz A dada por:
y llamamos matriz ampliada a la matriz
DAVID RIVIER SANZ
dada por:
3-3
TEMA 3: RESOLUCIÓN DE SISTEMAS DE ECUACIONES MEDIANTE DETERMINANTES.
2º BACH(CN)
Teorema de ROUCHÉ.El sistema (*) tiene solución si y sólo si rang( )=rang(
).
Ejemplos:
1)
2x 3 y z 4
x 2 y 5 tiene solución?
¿El sistema de ecuaciones
3y z 1
2 3
1 2
La matriz de coeficientes es A
0 3
1
0 y det( A )
1
2 3
Por otro lado la matriz ampliada es A
A
2
0
rang( A )
3.
1 4
1 2 0 5
y
rang( A ) 3 , ya que como
0 3 1 1
tiene tres filas su rango no puede ser mayor que 3 y la matriz A es un menor distinto de
cero de A .
Luego como rang( A )
rang( A ) entonces el sistema es compatible, es decir, tiene
solución.
2)
x 2y z 0
x y
1 ?
¿Y el sistema de ecuaciones
2x 3 y z 2
La matriz de coeficientes es A
1
2 1
1
1 0 y tenemos que el determinante se anula,
3 1
2
es decir, A
0
1
1
2
1
1 0
rang( A )
Por otro lado la matriz ampliada es A
1 1
orden 3, como por ejemplo 1 0
2 1
quiere decir que
2.
1
2 1 0
1
1 0
2
3 1 2
1 y si cogemos un menor de
0
1 , comprobamos que es distinto de cero, luego eso
2
rang( A ) 3 .
Por tanto, como
rang( A )
rang( A ) entonces el sistema es incompatible, es decir, no
tiene solución.
DAVID RIVIER SANZ
3-4
TEMA 3: RESOLUCIÓN DE SISTEMAS DE ECUACIONES MEDIANTE DETERMINANTES.
2º BACH(CN)
4.-REGLA DE CRAMER
La regla de Cramer es un teorema que nos permite obtener la solución de un sistema
de n ecuaciones y n incógnitas utilizando determinantes.
Definición: Sean A
a11
a 21
a12
a 22
... a1n
... a 2 n
...
a n1
...
an2
... ...
... a nn
y A
a11
a 21
a12
a 22
... a1n c1
... a 2 n c 2
...
a n1
...
an2
... ... ...
... a nn c n
la matriz de
coeficientes y la matriz ampliada respectivamente de un sistema de ecuaciones con n
incógnitas, x1 ,
c1
c2
a12
a 22
... a1n
... a 2 n
...
cn
...
an2
... ...
... a nn
a11
a 21
a12
a 22
... c1
... c 2
...
a n1
...
an2
... ...
... c n
Ax1
Axn
x 2 , ... , x n , definimos Ax1 como
, Ax2
a11
a 21
c1
c2
... a1n
... a 2 n
...
a n1
...
cn
... ...
... a nn
y así sucesivamente hasta
Teorema de CRAMER.Dado (*), un sistema de n ecuaciones con n incógnitas, en el que A
decir, con solución ( rang( A )
0 , es
rang( A ) ). Entonces la solución del sistema viene dada
por:
x1
Ax1
A
,
Ax2
x2
A
, …y
xn
Axn
A
2x 3 y z 4
x 2y 5 .
Ejemplo: Resuelve el sistema de ecuaciones
3y z 1
Como vimos en el ejemplo 1) del apartado anterior, el sistema es compatible, es decir,
tiene solución.
El det( A )
DAVID RIVIER SANZ
A
2
0 y además:
3-5
TEMA 3: RESOLUCIÓN DE SISTEMAS DE ECUACIONES MEDIANTE DETERMINANTES.
Ax
Luego
4 3
5 2
1
2
1 3
1
Ax
x
38 , Ay
38
2
A
2 4
1 5
1
2
0 1
1
2 3 4
1 2 5
1 y Az
17
0 3 1
Ay
19 , y
2º BACH(CN)
1
y z
2
A
Az
17
2
A
17
2
5.-DISCUSIÓN DE SISTEMAS MEDIANTE DETERMINANTES.
Caso general:
Dado un sistema de Cramer de orden n (es decir, con n ecuaciones y n incógnitas)
tenemos que:
(1) Si A
0
rang( A )
rang( A )
(2) Si A
0
rang( A )
n
n
Sistema compatible determinado (SCD).
Pueden pasar dos cosas:
(2a) Si
rang( A ) rang( A ) n
(2b) Si
rang( A )
rang( A )
Sistema compatible indeterminado (SCI).
Sistema incompatible (SI).
Caso particular y/o más frecuente, n=3:
Dado un sistema de Cramer de orden 3 (es decir, con 3 ecuaciones y 3 incógnitas)
tenemos que:
(1) Si A
0
rang( A )
(2) Si A
0
rang( A ) 3
rang( A )
3
Sistema compatible determinado (SCD).
Pueden pasar dos cosas:
(2a) Si
rang( A ) rang( A )
Sistema compatible indeterminado (SCI).
(2b) Si
rang( A )
Sistema incompatible (SI).
rang( A )
Observación: En el caso (2a) pueden ocurrir dos cosas:
(2a1)
rang( A ) rang( A ) 2
(2a2)
rang( A ) rang( A ) 1
En ambos, el sistema es compatible indeterminado
6.-SISTEMAS HOMOGÉNEOS.
Definición:
Se
llama
sistema
homogéneo
a
aquel
sistema
cuyos
términos
independientes son todos cero.
DAVID RIVIER SANZ
3-6
TEMA 3: RESOLUCIÓN DE SISTEMAS DE ECUACIONES MEDIANTE DETERMINANTES.
2º BACH(CN)
Propiedades:
1.-Un sistema homogéneo tiene, con seguridad, la solución trivial x1
x2
...
xn
0.
2.-Para que un sistema homogéneo tenga más soluciones que la trivial, es necesario y
suficiente que rang( A )
nº de incógnitas .
Ejemplo: Resolver
x
y
z
x
y 2z
0.
z 0
2x 4 y
A
1
1
1
1
1
2
2
4
1
0 , pero
0
1
1
1
1
2
0
rang( A )
2.
Entonces podemos suprimir la última ecuación (me quedo con las que son linealmente
independientes) y pasar la variable z al segundo miembro, quedándonos:
x y z
, sumando las ecuaciones nos queda 2 x
x y 2z
Si
x
3
ze y
2
1
z.
2
, tenemos infinitas soluciones, que dependerán del valor que yo asigne al
z
parámetro
x
3z
:
3
2
1
2
, y
y
.
z
7.-FORMA MATRICIAL DE UN SISTEMA DE ECUACIONES.
Dado el sistema de ecuaciones (*) lo podemos expresar matricialmente del siguiente
modo:
C donde A , X y C son las matrices siguientes
A X
A
a11
a 21
a12
a 22
... a1n
... a 2 n
...
a n1
...
an2
... ...
... a nn
,
x1
x2
...
xn
X
Además el sistema tiene como solución
x
Ejemplo:
y
z
x 3z
6
2x 5 y 3z
X
luego
A
2
0
x
y
8 8 3 6
9 5 2 2
32
64
z
5
34
x
DAVID RIVIER SANZ
2 1 0
32 , y 64 y z
y
C
X
A
1
1
1
0
2
5
c1
c2
...
cn
1
.
C.
1
3 ,C
3
6
2 y A
0
8 8 3
1
9
5 2
5
2 1
34
3-7