Tema B - Departamento de Matemáticas

Universidad de los Andes
Departamento de Matemáticas
AD
OR
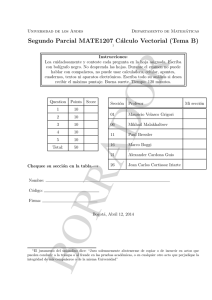
Primer Parcial MATE1207 Cálculo Vectorial (Tema B) 1
Instrucciones:
Lea cuidadosamente y conteste cada pregunta en la hoja asignada. Escriba
con bolı́grafo negro. No desprenda las hojas. Durante el examen no puede
hablar con compañeros, no puede usar calculadora, celular, apuntes,
cuadernos, textos ni aparatos electrónicos. Escriba todo su análisis si desea
recibir el máximo puntaje. Buena suerte. Tiempo: 120 minutos.
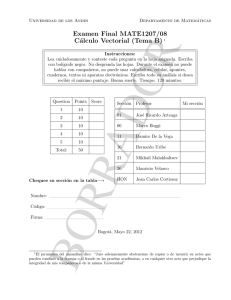
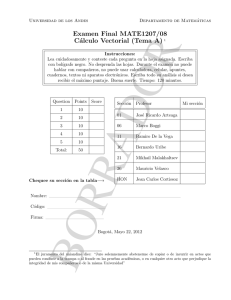
Points
1
10
2
10
3
10
4
10
5
10
Total:
50
Score
Chequee su sección en la tabla−→
Nombre:
Firma:
1
BO
Código:
Sección
Profesor
01
Mikhail Malakhaltsev
02
Jairo Andrés Angel Cardenas
03
Mauricio Velasco Grigori
04
Paul Bressler
05
Mainak Podder
06
John Richard Goodrick
RR
Question
Mi sección
Bogotá, Abril 20, 2013
El juramento del uniandino dice: “Juro solemnemente abstenerme de copiar o de incurrir en actos que
pueden conducir a la trampa o al fraude en las pruebas académicas, o en cualquier otro acto que perjudique la
integridad de mis compañeros o de la misma Universidad”
Código:
1. (10 points)
Tema B
Pág. 2 de 15
Si su respuesta y justificación son correctas obtendrá el máximo puntaje. Si su res-
puesta es incorrecta podrá obtener créditos parciales de acuerdo a su justificación.
Resp.
AD
OR
Encontrar el volumen del sólido entre el paraboloide z = 1 − x2 − y 2 y el plano z = −3.
Solution: La intersección del plano z = −3 y el paraboloide z = 1 − x2 − y 2 es la
circunferencia z = −3, x2 + y 2 = 4.
El sólido es acotada por las gráficos de las funciones z = y z = x2 + y 2 − 1 sobre la
región D = {(x, y) | x2 + y 2 ≤ 4}.
Entonces, el volumen es
ZZ
ZZ
2
2
4 − x2 − y 2 dxdy.
V =
1 − x − y − (−3) dxdy =
D
D
Pasamos a las coordenadas cilı́ndricas. La región D = {(r, θ) | 0 ≤ r ≤ 2, 0 ≤ θ ≤ 2π}.
ZZ
Z 2π Z 2
Z 2
2
2
V =
(4 − r ) r drdθ =
(4 − r ) r dr dθ = 2π
(4 − r 2 ) r dr = 8π.
0
0
0
RR
D
8π
Pautas de corrección:
Reglas generales:
Cada error en cálculo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . -2
BO
Cada error aritmético . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . -1
El “camino” sin solución correcta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0
Créditos parciales:
Evaluación de la integral con coordenadas
a) cilı́ndricos:
Planteamiento de la integral . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
que incluye: los lı́mites correctos para r (2), los lı́mites correctos para z (2), los lı́mites
correctos para θ (1), el integrando correcto (1), el orden de dz, dr y dθ correcto (1).
Cada paso de integración (bajo la condición que el planteamiento es correcto) . . . . . . 1
Problema 1 continúa en la página siguiente. . .
Prob. 1 cont.. . .
Código:
Tema B
Pág. 3 de 15
b) cartesianas:
AD
OR
Planteamiento de la integral . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
que incluye: los lı́mites correctos para x (1), los lı́mites correctos para y (1), los lı́mites
correctos para z (2), el integrando correcto (1).
Evaluación de la integral . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
BO
RR
donde evaluación de la integral de cos4 θ vale 3.
Problema 1 continúa en la página siguiente. . .
Código:
Tema B
BO
RR
AD
OR
Prob. 1 cont.. . .
Pág. 4 de 15
Código:
Pág. 5 de 15
Si su respuesta y justificación son correctas obtendrá el máximo puntaje. Si su respuesta es incorrecta podrá obtener créditos parciales de acuerdo a su justificación.
AD
OR
Suponga que la temperatura en un punto de una plaquita esta dada por la función f (x, y) =
4 + x2 + y 2 − 4y.
(a) (5 points) Encuentre el punto más caliente y el más frı́o en la circunferencia x2 + y 2 =
16 y los valores de temperatura en estos puntos.
(b) (5 points) Encontrar los puntos más calientas y más frı́os de la región
R = {(x, y) | x2 + y 2 ≤ 16}
y los valores de temperatura en estos puntos.
Resp. (a)
Resp. (b)
Solution:
Opción 1. La función f (x, y) = x2 + (y − 2)2 es el cuadrado de la distancia entre el
punto (x, y) y el punto (0, 2), entonces es obvio que el punto más caliente es (0, −4) con
la temperatura 36 y el punto más frı́o es (0, 4) con la temperatura 4.
RR
En la región el punto más frı́o es (0, 2) con la temperatura 0.
Opción 2. La parametrización de la circunferencia es x = 4 cos t, y = 4 sin t, t ∈ [0, 2π].
Entonces se puede tomar la función g(t) = f (4 cos t, 4 sin t) = 20 − 16 sin t.
Por la propiedades del coseno, la función g(t) toma el máximo en t = 3π/2 y g(3π/2) =
36. Entonces f (x, y) toma el máximo en el punto (0, −4) y el valor maximal es 36. El
mı́nimo de g(t) es t = π/2, entonces el punto más frı́o es (0, 4) y la temperatura es 4.
En la región el punto crı́tico de la función encontraremos del sistema
∂f
= 2x = 0,
∂x
BO
2.
Tema B
∂f
= 2y − 4 = 0,
∂y
entonces f (x, y) tiene solamente un punto crı́tico que es (0, 2) y f (0, 2) = 0.
Opción 3. El método de multiplicadores de Lagrange. Hacemos la función
F (x, y, λ) = 4 + x2 + y 2 − 4y + λ x2 + y 2 − 16
Sus puntos crı́ticos se puede encontrar del sistema

 ∂F
 x(1 + λ) = 0
 ∂x = 2x + 2λx = 0
∂F
y(1 + λ) − 2 = 0
⇒
=
2y
−
4
+
2λy
=
0
∂x
 2
 ∂F
2
2
x + y 2 − 16 = 0
= x + y − 16 = 0
∂λ
Problema 2 continúa en la página siguiente. . .
Prob. 2 cont.. . .
Código:
Tema B
Pág. 6 de 15
AD
OR
De la primera ecuación x = 0 o 1 + λ = 0. Si 1 + λ = 0 entonces de la segunda ecuación
obtenemos contradicción. Entonces, x = 0 y tenemos dos soluciones y = 4, λ = 1/2 y
y = −4, λ = −3/2. Evaluamos la función en los puntos A(4, 0) y B(−4, 0): f (A) = 4,
f (B) = 36.
En la región el punto crı́tico de la función encontraremos del sistema
∂f
= 2x = 0,
∂x
∂f
= 2y − 4 = 0,
∂y
entonces f (x, y) tiene solamente un punto crı́tico que es (0, 2) y f (0, 2) = 0.
Resp. (a)
Resp. (b)
máx (0, −4), fmax = 36; mı́n (0, 4), fmin = 4
máx (0, −4), fmax = 36; mı́n (0, 2), fmin = 0
Pautas de corrección:
Reglas generales:
Cada error en cálculo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . -2
Cada error aritmético . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . -1
RR
El “camino” sin solución correcta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0
Créditos parciales:
a) El sistema de ecuaciones del método de multiplicadores de Lagrange es correcto . 2
La solución del sistema es correcta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
La respuesta final es correcta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1
b) El sistema de ecuaciones para encontrar los puntos crı́ticos es correcto . . . . . . . . . . . 2
La solución del sistema es correcta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
La respuesta final es correcta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1
BO
Falta la verificación que el punto critico pertenece a la región . . . . . . . . . . . . . . . . . . . . . . -1
Problema 2 continúa en la página siguiente. . .
Código:
Tema B
BO
RR
AD
OR
Prob. 2 cont.. . .
Pág. 7 de 15
Código:
Pág. 8 de 15
Si su respuesta y justificación son correctas obtendrá el máximo puntaje. Si su respuesta es incorrecta podrá obtener créditos parciales de acuerdo a su justificación.
AD
OR
Sea R un paralelogramo en el plano xy acotado por las rectas y = −2x, x = −2y, y =
−2x − 3, x = 3 − 2y.
(a) (4 points) Dibujar el paralelogramo R y su imagen S bajo la transformación
u = 2x + y,
v = x + 2y.
(b) (6 points) Usar la transformación para evaluar la integral
ZZ
1
(2x + y) ey+ 2 x dA.
R
Resp. a)
plano xy
plano uv
y
v
3
3
2
2
1
−2
−3
−1
1
0
1
2
−1
x
3
−2
a)
0
1
plano xy
3
2
S
1
−2
−1
u
v
3
−3
3
plano uv
y
R
2
−3
RR
Solution:
−1
−2
−3
b)
−2
−3
−1
BO
3.
Tema B
0
1
2
1
2
3
x
−3
−2
−1
0
−1
−1
−2
−2
−3
−3
1
2
3
u
b) La matriz de Jacobi de la transformación u = 2x + y, v = x + 2y es
D(u, v)
2 1
=
1 2
D(x, y)
Problema 3 continúa en la página siguiente. . .
Prob. 3 cont.. . .
Código:
Tema B
Pág. 9 de 15
AD
OR
−1
D(x,y)
= det D(u,v)
= 1/3.
entonces el jacobiano es J = det D(u,v)
D(x,y)
Por lo tanto,
ZZ
ZZ
Z Z 3
1
1
3
1 0
1
v
v
y+ 21 x
dA =
ue 2 ( )dudv =
(2x + y)e
ue 2 dv du = 3[1 − e 2 ].
3
3 −3 0
S
R
Pautas de corrección:
Reglas generales:
Cada error en cálculo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . -2
Cada error aritmético . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . -1
El “camino” sin solución correcta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0
Créditos parciales:
a) Cada dibujo correcto . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
b) Todo es correcto pero falta el jacobiano en el integrando . . . . . . . . . . . . . . . . . . . . . . . . .5
BO
RR
Todo es correcto pero faltan el cálculo del jacobiano y el jacobiano en el integrando 4
Problema 3 continúa en la página siguiente. . .
Código:
Tema B
BO
RR
AD
OR
Prob. 3 cont.. . .
Pág. 10 de 15
Código:
4. (10 points)
Tema B
Pág. 11 de 15
Si su respuesta y justificación son correctas obtendrá el máximo puntaje. Si su res-
AD
OR
puesta es incorrecta podrá obtener créditos parciales de acuerdo a su justificación.
Hallar la masa del sólido dado por las disigualidades x2 + y 2 + z 2 ≤ 4, x2 + y 2 − z 2 ≤ 0,
z ≥ 0 que tiene la función de densidad δ(x, y, z) = z + 1.
Resp.
Solution: El sólido es una parte de cono acotado por la esfera:
z
RR
La seccion del sólido por el plano y = 0 nos da
BO
x
Entonces en las coordenadas esféricas el solido se describe como 0 ≤ ρ ≤ 2, 0 ≤ φ ≤ π/4,
0 ≤ θ ≤ 2π.
Luego la masa de sólido E es (usamos las coordenadas esféricas):
M=
ZZZ
d(x, y, z)dV =
E
ZZZ
(z + 1)dV =
E
=
Z
0
2π
Z
0
π/4
Z
0
2
(ρ cos φ + 1)ρ2 sin φ drdφdθ = 2π
√ !
11 − 4 2
.
3
Problema 4 continúa en la página siguiente. . .
Prob. 4 cont.. . .
Código:
Respuesta:
Pág. 12 de 15
√ 11−4 2
3
AD
OR
2π
Tema B
Pautas de corrección:
Reglas generales:
Cada error en cálculo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . -2
Cada error aritmético . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . -1
El “camino” sin solución correcta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0
Créditos parciales:
Planteamiento de la integral: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1 punto para sólo escribirlo cómo la integral triple sobre E de 1 − z ó 1 + z.
5 puntos más para convertirlo en integral triple:
En coordenadas esféricas, 1 punto para cada par de lı́mites correctos (=3 puntos, uno
para cada variable), 1 punto más para el factor de ρ2 sen(φ) o de r, y (en coordenadas
esféricas) el último punto para convertir z en ρ cos(φ).
RR
En coordenadas cilı́ndricas, 4 puntos para armar correctamente los lı́mites de integración
(1 punto para los lı́mites de z, 1 punto para los lı́mites de θ, y 2 para los lı́mites para r).
Luego 1 punto más para el factor adicional de r. (¡En cilı́ndricas, no hay que convertir
la variable z!)
Evaluación de la integral: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
BO
1 punto para integrar dθ, 1 punto para integrar dρ o dr, y 2 puntos para dφ o dz.
Problema 4 continúa en la página siguiente. . .
Código:
Tema B
BO
RR
AD
OR
Prob. 4 cont.. . .
Pág. 13 de 15
Código:
Pág. 14 de 15
No hay créditos parciales. Las cinco partes no están relacionadas.
(a) (2 points) (a)
(b) (2 points) (b)
R 1 R x2
0
0
f (x, y) dy dx =
R1RπRπ
0
0
AD
OR
Llene la casilla en blanco con F (Falso) o V (Verdadero), según sea el caso.
0
R 1 R √y
0
0
f (x, y) dx dy. . . . . . . . . . . . . . . . . . . . . . . .
ρ2 sin ϕ dθ dϕ dρ = 2π/3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
(c) (2 points) (c) En el punto (0, 0) la función f (x, y) = x2 + 2xy + 4y 2 crece en cada
dirección. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
RRR
(d) (2 points) (d)
xdV = 0 donde R = {(x, y, z) | (x − 2)2 + y 2 + z 2 = 1}. . . . . . .
R
(e) (2 points) (e) El punto (0, 1) es un punto crı́tico de la función f (x, y) = 2x + 3y.
Solution:
(a)
(b)
R 1 R x2
0
0
f (x, y) dy dx =
R1RπRπ
0
0
0
R 1 R √y
0
0
f (x, y) dx dy. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . F
ρ2 sin ϕ dθ dϕ dρ = 2π/3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . V
(d)
RRR
R
RR
(c) En el punto (0, 0) la función f (x, y) = x2 + 2xy + 4y 2 crece en cada dirección. V
xdV = 0 donde R = {(x, y, z) | (x − 2)2 + y 2 + z 2 = 1}. . . . . . . . . . . . . . . . . F
(e) El punto (0, 1) es un punto crı́tico de la función f (x, y) = 2x + 3y. . . . . . . . . . F
BO
5.
Tema B
Problema 5 continúa en la página siguiente. . .
Código:
Tema B
BO
RR
AD
OR
Prob. 5 cont.. . .
Pág. 15 de 15