2.2. Parametrización de superficies explicitas e implícitas.

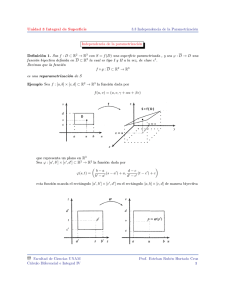
2.2. Parametrización de superficies explicitas e implícitas.
Las superficies S pueden estar dadas también de manera explicita o implicita en ℜ3 .
Cuando una superficie está dada de manera que un conjunto de puntos
( x, y , z )
satisfacen la ecuación F ( x, y, z ) = 0 , se dice que la superficie está representada en
forma implícita. Si de esta ecuación podemos despejar una de las variables en función
de las otras dos, por ejemplo, z = f ( x, y ) , entonces se dice que la superficie esta dada
en forma explicita. Para realizar la parametrización de una superficie que esté dada de
manera explicita de las formas x = f ( y, z ) , y = f ( x, z ) ó z = f ( x, y ) , se puede
utilizar como referencia la expresión genérica que se presentan en la Tabla 2.
Tabla 2. Parametrización de una Superficie dada de forma explicita.
Superficie Explicita S
z = f ( x, y )
Parametrización de la Superficie S
 u   x


g : ℜ → ℜ / g ( u , v ) =  v  =  y  ,
 f ( u, v )   z 
2
3
con a ≤ u ≤ b y c ≤ v ≤ d
Fuente: Propia.
Para las superficies dadas de manera implícita se puede recurrir a la representación de
este tipo de superficies en coordenadas cilíndricas, coordenadas esféricas, u otro tipo de
parametrización conveniente; algunas de las parametrizaciones más utilizadas se
muestran en la Tabla 3, aunque cabe señalar que no es la única parametrización que se
puede realizar de las superficies a las cuales se hace referencia.
Tabla 3. Parametrización de Superficies dadas de Forma Implícita.
Cono
z 2 = x2 + y2
 r cos (θ )   x 


g : ℜ2 → ℜ3 / g ( r ,θ ) =  rsen (θ )  =  y  , con
 r
  z 
r1 (θ ) ≤ r ≤ r2 (θ ) y 0 ≤ θ ≤ 2π
 asen (θ )   x 


g : ℜ → ℜ / g ( z ,θ ) =  a cos (θ )  =  y  , con

  z 
z
2
Cilindro
x2 + y 2 = a2
3
0 ≤ θ ≤ 2π y z1 ≤ z ≤ z2
Tabla 3. (Continuación)
 a s en (ϕ ) cos (θ )   x 


g : ℜ → ℜ / g (θ , ϕ ) =  a s en (ϕ ) sen (θ )  =  y  ,

  z 
a cos (ϕ )
2
Esfera
x2 + y 2 + z 2 = a2
3
con 0 ≤ θ ≤ 2π y 0 ≤ ϕ ≤ π
Fuente: Propia.
EJEMPLO 46. Realice la parametrización de la superficie dada por el paraboloide
z = 5 − x 2 − y 2 que se encuentra por arriba del plano xy.
Solución.
Se tiene aquí una superficie dada en forma explicita de la forma z = f ( x, y ) , por lo
tanto una parametrización conveniente para esta superficie viene dada por la función
g : ℜ2 → ℜ3 / g ( u, v ) = ( u, v,5 − u 2 − v 2 ) = ( x, y, z )
Figura 48. Paraboloide del Ejemplo 46.
EJEMPLO 47. Parametrizar la superficie definida por el cilindro x 2 + z 2 = 4 , entre
plano x + y = 1 , y el plano xz.
Solución.
La superficie que se desea parametrizar es la poción de la superficie del cilindro
x 2 + z 2 = 4 que se encuentra entre el plano x + y = 1 denotado por S2 , y el plano xy
identificada como S3 . Una parametrización para la superficie del cilindro S1 está dada
al
emplear
las
coordenadas
cilíndricas
definiendo
la
función
 2 sen (θ )   x 


g1 : ℜ → ℜ / g1 ( y,θ ) =  2 cos (θ )  =  z  , como la parametrización de esta superficie

y   y 
2
3
en donde 0 ≤ θ ≤ 2π , y 0 ≤ y ≤ 1 − 2 sen (θ ) , debido a que el cilindro está acotado por el
plano y = 1 − x y el plano xz, y = 0
Figura 49. Superficie del Ejemplo 47.
EJERCICIO PROPUESTOS 2.2.
Realice una parametrización para las superficies que se presentan a continuación:
1) El cilindro z 2 + y 2 = 9 , entre los planos x = −2 y x = 3 .
2) El paraboloide 9 − 2 z 2 − 3 x 2 = y , que se encuentra para y ≥ 0 .
3) El cono truncado x 2 + y 2 = z 2 , entre los planos x = −2 y x = 3 .
4) El hemisferio z = − 4 − x 2 − y 2 .