Estabilidad Relativa (Nyquist Reducido)

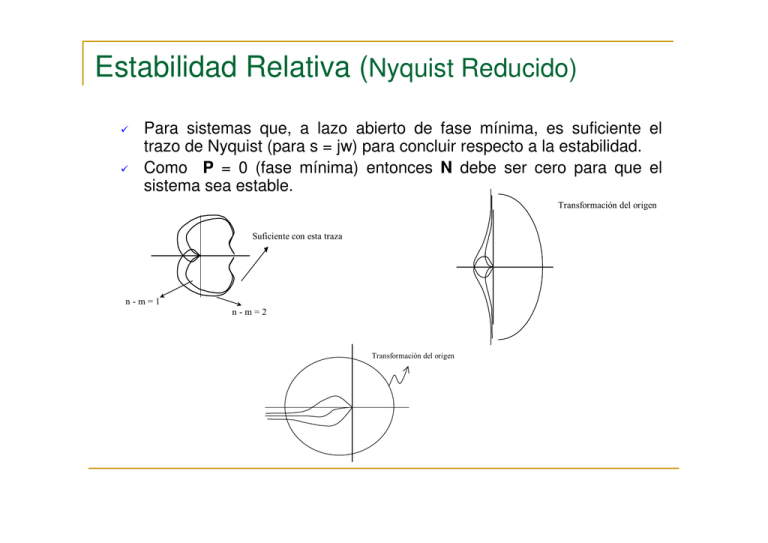
Estabilidad Relativa (Nyquist Reducido)
Para sistemas que, a lazo abierto de fase mínima, es suficiente el
trazo de Nyquist (para s = jw) para concluir respecto a la estabilidad.
Como P = 0 (fase mínima) entonces N debe ser cero para que el
sistema sea estable.
Transformación del origen
Suficiente con esta traza
n-m=1
n-m=2
Transformación del origen
Estabilidad Relativa (Nyquist Reducido)
1 Kg
Margen de
ganancia positivo
-1
γ
φ
γ Margen de fase
positivo
Margen de
fase γ
negativo
-1
1 Kg
Margen de
ganancia
negativa
Estabilidad Relativa (Nyquist Reducido)
1 Kg
Margen de
ganancia positivo
-1
γ
γ
Margen de fase
positivo
Margen de
fase γ
negativo
-1
1 Kg
φ
Margen de
ganancia
negativa
Estabilidad Relativa
Margen de Ganancia
Es el inverso de la magnitud de |G(jω)| en la frecuencia en la cual la fase vale φ = -180º
ω1 → φ(w1) = -180º
Kg (dB) = 20 lg Kg = -20 log |G(jω1)|
Margen de Fase
Es la cantidad de atraso (φ negativa) en la frecuencia de cruce ( |G(jω1)| = 1)
requerida para llevar al sistema al límite de la estabilidad.
γ = 180º + φ
Bode Diagrams
El sistema es estable, pues ambos
márgenes son positivos.
Gm = Inf, Pm=35.477 deg. (at 22.985
rad/sec)
50
Phase (deg); Magnitude (dB)
20 lg | GH | = 0 db φ ≈ -143º
→γ = 180º - 143º = 37º
φ→ -180º 20 lg |G| → - ∞ db
→MG = ∞ (+)
75
25
0
-25
-60
-80
-100
-120
-140
-160
-180
10-2
10-1
100
Frequency (rad/sec)
101
102