Notas de Integrales y Funciones Elipticas

Notas de Integrales y Funciones
Elípticas
Erika Fernández Gómora
Septiembre 2005
ii
Índice general
Introducción
V
I
1
Integrales Elípticas
1. Leyes de Kepler
5
2. Métodos numéricos para aproximar integrales elípticas
2.1. Aproximación de la longitud de la grá…ca del sen(x) en el intervalo
[0,2 ] usando Expansión de Taylor . . . . . . . . . . . . . . . . .
2.2. Aproximación de la longitud de la grá…ca del sen(x) en el intervalo
[0,2 ] usando el Método del Trapezoide . . . . . . . . . . . . . .
2.3. Promedios aritmético-geométricos. . . . . . . . . . . . . . . . . .
2.4. EJEMPLOS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
3. Integrales elípticas en problemas de la Mecánica, la Geometría
y la Dinamica de Fluidos.
3.1. Oscilaciones de un péndulo sin fricción . . . . . . . . . . . . . . .
3.2. Encontrar el área de la super…cie de la sección separada del cilindro x2 +z2 =a2 por el cilindro x2 +y2 =b2 , donde 0 < b < a y
z 0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3. Ondas viajeras para la ecuación de Korteweg - de Vries . . . . .
II
Funciones Elípticas
9
10
11
12
15
15
19
21
25
4. Mapeos del Semiplano Superior H +
27
5. Sinus Amplitudinus
37
5.1. ¿Cuál es el orden de los polos de sn(z;k)? . . . . . . . . . . . . . 39
5.2. ¿Cómo ajustar K(k) y K’(k) para tener como dominio un cuadrado, es decir, tal que K(k)=2K’(k)? . . . . . . . . . . . . . . . . . 42
5.3. Funciones meromorfas con polos y ceros dobles. . . . . . . . . . . 44
5.3.1. ¿Qué se puede decir de una función meromorfa g(z) con
polo doble en A + iA y cero doble en cero? . . . . . . . . 44
iii
iv
ÍNDICE GENERAL
5.3.2. ¿Qué otras funciones meromorfas m(z) tienen un cero
doble en 0 y un polo doble en A + iA? . . . . . . . . . . .
5.3.3. ¿Cuántas funciones elípticas con periodos 2A y 2iA
tienen un cero doble en 0 y un polo doble en A + iA? . .
44
45
6. Función P de Weierstrass
47
6.1. Ecuación Diferencial para P (z) . . . . . . . . . . . . . . . . . . . 48
6.2. Ecuación Diferencial para P . . . . . . . . . . . . . . . . . . . . . 48
7. Función Theta
51
7.1. Ecuación de Calor . . . . . . . . . . . . . . . . . . . . . . . . . . 51
7.2. Propiedades de las funciones T HET A . . . . . . . . . . . . . . . 53
8. Hacia el problema de inversión
57
8.1. Funciones Elípticas de Grado 1 . . . . . . . . . . . . . . . . . . . 58
8.2. Funciones Elípticas de Grado 2 . . . . . . . . . . . . . . . . . . . 59
8.3. Función P de Weierstrass . . . . . . . . . . . . . . . . . . . . . . 60
A. Korteweg-de Vries
65
Bibliografía
71
Introducción
Las integrales y funciones elípticas aparecen de manera natural cuando se
trata de resolver una gran cantidad de problemas geométricos y físicos, como
veremos a lo largo de estas notas.
v
vi
INTRODUCCIÓN
Parte I
Integrales Elípticas
1
3
El origen del término se debe a que hacen su aparición en el contexto de calcular
de manera aproximada la longitud de una elipse.
Calculemos esta longitud para conocer la integral elíptica que llamaremos del
segundo tipo. Tomando como parametrización de la elipse (t) = (a cos(t); b
sen(t)) con b > a > 0
t 2 [0; 2 ], la longitud queda dada por:
Z 2
Z 2
p
p
2
2
2
2
a sen (t) + b cos (t)dt = 4
a2 sen2 (t) + b2 (1 sen2 (t))dt
L(a; b) = 4
0
0
Z 2
Z 2
p
p
=4
b2 + a2 sen2 (t) b2 sen2 (t)dt = 4
b2 + (a2 b2 )sen2 (t)dt
0
0
Z 2q
Z 2
p
2
2
1 ( b b2a )sen2 (t)dt = 4b
1 k 2 sen2 (t)dt
= 4b
0
tomando k 2 =
0
b2 a2
b2
a2
b2 ,
=1
que es la excentricidad de la elipse.
Z 2
p
A las integrales de este tipo, es decir a las de la forma
1 k 2 sen2 ( )d
0
con 0 < k < 1 las llamaremos integrales elípticas completas del segundo tipo.
Este tipo de integrales tambien las encontramos al calcular la longitud de la
grá…ca de la función sen(x) en el intervalo 0; 2 :
L(sen(x); 0; 2 ) =
=
Z
Z
2
0
2
p
p
1 + cos2 (x)dx =
2
0
Z
2
p
1 + (1
Z 2r
p
sen2 (x)dx = 2
1
0
0
sen2 (x))dx
p1
2
2
sen2 (x)dx
L(sen(x); 0; 2 ) es una integral del segundo tipo con k = p12
Hasta ahora estas integrales han aparecido en problemas geométricos pero la
motivación surge de la Mecánica Celeste, en los trabajos de Kepler sobre el
movimiento de los planetas.
4
Capítulo 1
Leyes de Kepler
El problema de describir el movimiento de los planetas se remonta a los Griegos
quienes creían que los planetas giran alrededor de la tierra en órbitas círculares.
Fue hasta 1543, que Copérnico propone al Sol como el cuerpo alrededor del cual
giran los planetas. Aún así, Copérnico mantenía la idea de los griegos con respecto a la órbita que siguen los planetas que es el Sistema Ptolemaico de Epiciclos y
Deferentes. Segun este Sistema los planetas giran en orbitas circulares pequeñas
(Epiciclos) cuyo centro gira alrededor de una órbita circular (Deferentes) mayor
centrada en el Sol. La utilización de este sistema requeria ajustar el número de
epiciclos cada vez que los datos observacionales no coincidian con la teoría Por
lo tanto era muy di…cil predecir la posición de los cuerpos a tiempos futuros.
Fue Kepler quien trabajando con el reconocido astrónomo Tycho Brahe, propone
un modelo a partir de los datos observacionales. Brahe le asignó el proyecto de
calcular la órbita de Marte [Ca].
Marte era el planeta que mostraba más diferencias entre los datos observacionales y la teoría que se tenía hasta ese momento, e.d. el modelo de Copérnico.
A Kepler le interesaba conocer la posición de Marte con respecto al tiempo.
Si P (0) es la posición del planeta al tiempo 0
(i) ¿Cuál es la posición a un tiempo t
0? Es decir, ¿Podremos parametrizar
la posición del cuerpo como una función del tiempo P (t) = (x(t); y(t))?
(ii) ¿Podemos conocer la distancia recorrida por Marte del tiempo t0 = 0 al
tiempo t?
Depués de estudiar los datos observacionales recavados por Brahe, Kepler formuló sus Tres Leyes del Movimiento Planetario:
1a Los cuerpos celestes se mueven en trayectorias elípticas sobre un plano y
el Sol es un foco de dicha órbita.
2a A tiempos iguales se barren áreas iguales
5
6
CAPÍTULO 1. LEYES DE KEPLER
3a El cuadrado del periodo de revolución de cualquier planeta es proporcional
al cubo del semieje mayor de la elipse determinada por el movimiento de
dicho planeta alrededor del Sol.
La primera ley de Kepler contesta la pregunta (i) y (ii), podemos parametrizar
la posición de Marte como P (t) = (a cos( (t)); b sen( (t)) ) y la distancia
recorrida por Marte durante el tiempo t to esta dada por:
Z t
p
L(a; b) =
a2 sen2 (s) + b2 cos2 (s) (s)ds =
to
Z t s
2
q
b2 a2
1
=b
sen2 (s) (s)ds
b2
to
=b
Z
t
s
1
0
q
2
b2 a2
b2
sen2 (s) (s)ds
(0)
A las integrales que aparecen en este contexto las llamamos integrales incompletas del segundo tipo.
Pero aun no sabemos cómo es (t). Lo que sí sabemos por la tercera ley de
Kepler es que el movimiento no es uniforme así que (t) no es constante.
Utilicemos la Mecánica Newtoniana para encontrar (t):
La ley de Gravitación nos dice que cualesquiera dos particulas con masa M y
m respectivamente se atraen mediante la siguiente relación
F = G MRm
2
con G una constante y r la distancia entre las dos partículas.
Mientras que la segunda ley de Newton: Una Fuerza F actuando en una masa
m le da a la masa una aceleración a y se tiene
F = ma
Sea M = masa del Sol; m = masa de M arte, podemos pensar al Sol y a Marte
como partículas ya que su masa es pequeña con respecto a la distancia entre los
dos cuerpos. Si tomamos F como la f uerza gravitacional tenemos:
M
GR
2 = a
En nuestro caso, la aceleración actua en la misma dirección del vector Marte-Sol
y en dirección de decrecimiento de R(t):
7
Por lo que la aceleración es una función del Radio R. Ya que
2
a(R) = R(t)
R(t) (t)
2
R(t)
R(t) (t) =
GM
R(t)2
(1)
Pero la gravitación actua radialmente por lo cual la aceleración no es una función
del ángulo . Es decir
a( ) =
1
R(t)
d
dt
R2 (t) (t)
=0
de esta última ecuación encontramos que
R(t)2 (t) = c ; para alguna c 2 R
(2)
Nos gustaria tener una ecuación diferencial que solo involucre a R o a : Para
esto, utlicemos la relación
R=
h
1+e cos( )
donde
e = eccentricidad de la elipse def inida por la trayectoria de M arte
h = e (la distancia del Sol a la directriz de la elipse def inida por la
trayectoria de M arte)
sustituyendo en (2) obtenemos
(t) = c
k
1 + e cos( )
d
(1+e cos( ))2
)
Z
2
c
= ( )2 (1 + e cos( ))2
h
(3)
= ( hc )2 dt
ds
(1+e cos(s))2
= t ( hc )2
0
Ya se ve complicada la ecuacion de y recordemos que para nuestro problema
de encontrar la distancia recorrida por Marte en un intervalo de tiempo (0; t) lo
que nos interesa es (t).
8
CAPÍTULO 1. LEYES DE KEPLER
Para …nes prácticos, supongamos que el movimiento es uniforme, es decir (t) =
m; p:a m 2 R+ ;para obtener:
2
Z
4
L(a; b) = b m
t
s
1
0
q
2
b2
a2
b2
3
sen2 (s)ds5
=bm
Z
t
0
p
1
k 2 sen2 (s)ds
La distancia recorrida por marte esta dada por una integral que llamaremos
elíptica incompleta del segundo tipo.
A continuación describiremos algunos métodos para evaluar integrales elípticas
completas. El primer método sera para k pequeño usando expansión de Taylor
y el segundo sera para k 2 [0; 1] usando métodos númericos.
Capítulo 2
Métodos numéricos para
aproximar integrales
elípticas
2.1.
Aproximación de la longitud de la grá…ca
del sen(x) en el intervalo [0,2 ] usando Expansión de Taylor
La longitud de la grá…ca del sen(x) en el intervalo [0; 2 ] esta dada por:
I=
=
Si k =
p1 ,
2
Z
p
2
0
2
p
1 + cos2 (t)dt =
Z
2
q
1
0
Z
2
p
1 + (1
0
sen2 (t))dt =
( p12 )2 sen2 (t))dt
entonces
I=
p
2
Z
2
0
p
1
k 2 sen2 (t)dt. Sea f (x) = (1 + x)s .
Usando series de Taylor obtenemos:
f (x) = 1 + sx +
Rn =
s(s 1) 2
2! x
+
+
s(s 1)(s 2):::(s n+2) n 1
x
(n 1)!
s(s 1)(s 2):::(s n+1)(1+ )s
n!
9
n
xn ;
2 (0; x)
+ Rn
10CAPÍTULO 2. MÉTODOS NUMÉRICOS PARA APROXIMAR INTEGRALES ELÍPTICAS
Esta serie converge absolutamente si jxj
1: Por lo tanto x = k 2 sen2 ( )
cumple la condición para tener convergencia absoluta de la serie.
Sea s = 1=2
Z 2
2
3
1 1 1
1 1 1 3
2
2
2
2
p1 I =
1 ( 21 ) k 2 sen2 ( ) + 2!
2 2 k sen ( )
3! 2 2 2 k sen ( ) +
2
0
1 1
+::::: + ( 1)n n!
2
Rn =
1
3 2n
2 ::: 2
( 1)n (1+ )s
n!
2n
n
n
k 2 sen2 ( )
n+1
Y
dx + Rn
3) k 2n sen2n
(2i
i=2
jRn j
2.2.
1 1
n! 2n
n+1
Y
3) k 2n =
(2i
1 1
n! 2n
i=2
n+1
Y
(2i
3) k 2n
i=2
Aproximación de la longitud de la grá…ca
del sen(x) en el intervalo [0,2 ] usando el
Método del Trapezoide
Sean
fxo = 0; x1 =
2n ; x2
=
n ; x3
=
3
2n ; :::; xi
=
i
2n ; :::; xn
=
2g
una partición de [0; 2 ] y
yi = f (xi ) =
Entonces
Z 2
p
k 2 sen2 (t)dt
1
0
p
1
4n
k 2 sen2 (xi )
; 8i = 0; 1; 2; :::; n
[yo + 2y1 + 2y2 + ::: + 2yj + ::: + 2yn
1
+ yn ]
Una cota para el error utilizando este método es :
error
E
M ( =2)3
12n2 ,
M = maxfjf 00 (x)j ; 0
x
2g
Pero
jf 00 (x)j =
k2 (
cos2 (x)+sen2 (x)+k2 sen4 (x))
(1+k2 sen2 (x))3=2
k 2 sen2 (x) + k 2 sen4 (x)
k 2 sen2 (x) + k 2 sen4 (x)
cos2 (x)
por lo tanto
E
k2 [1+k2 ]
96n2
3
k2 1 + k2
cos2 (x)
2.3. PROMEDIOS ARITMÉTICO-GEOMÉTRICOS.
11
En el caso de la longitud de la grá…ca del sen(x) en el intervalo [0; =2] teniamos
que k = p12 por lo tanto el error esta acotado por
3
128n2
0;24223653656484231 n12
Comparación de la aproximación de
p
2
Z
do del trapezoide y expansión de Taylor.
n
1
2
3
5
9
15
50
Trapezoide
Estimación
1.8961188979370398
1.9099718215899177
1.9100969337379137
1.9100988937464334
1.9100988945138557
1.9100988945138557
1.9100988945138553
2
p
1
0
Error
0.242237
0.0605591
0.0269152
0.00968946
0.00299057
0.00107661
0.0000968946
k 2 sen2 (t)dt utilizando méto-
Expansión de Taylor
Estimación
1.9437612854442854
1.9177287682285138
1.9123053271418946
1.9103552187355535
1.9101049729345663
1.9100989330881069
1.9100988945138562
Error
0.25
0.09375
0.0390625
0.00769043
0.000362247
.0000440870
7.06894 x 10
Observamos que para n pequeña el método del Trapezoide nos da una mejor
estimación del error que por Expansión de Taylor pero conforme n crece Taylor
es quien da la mejor estimación del error.
2.3.
Promedios aritmético-geométricos.
Ya vimos que calcular la longitud de una elipse (e.d. calcular L(a; b)) no es un
problema sencillo. Gauss, Ramanujan, Landen y muchos otros grandes matemáticos dieron métodos para aproximar estas integrales. Uno de los más sencillos y
útiles es el de promedios Aritmético-Geométricos debido a Gauss.
¿Qué son estos promedios?
Tomemos a; b 2 R , a > b > 0: Consideremos la siguiente sucesión de promedios
an 1 +bn 1
aritméticos fai ja1 = a+b
8n > 1gi2N y la siguiente suceción
2 y an =
p2
p
de promedios geométricos fbi jb1 = ab y bn = an 1 bn 1 8n > 1gi2N :Es un
ejercicio probar que la sucesión fai g es decreciente y acotada inferiormente por
b mientras que la sucesión fbi g es creciente y acotada superiormente por a. Por
lo tanto ambas sucesiones convergen. No solo eso, si el lector hizo el ejercicio
habra notado que:
b < b1 < b2 < b3 < ::::::: < a3 < a2 < a1 < a
y que las suceciones convergen al mismo límite. Este límite, que denotaremos
por M (a; b), es el promedio aritmético-geométrico.(1 ).
1 American
Mathematical Monthly 1988. No.August-September. Pp585-608
17
12CAPÍTULO 2. MÉTODOS NUMÉRICOS PARA APROXIMAR INTEGRALES ELÍPTICAS
¿Qué tienen que ver estos promedios con nuestro problema original: Calcular el
perímetro de un elipse?
¡¡TODO!! El siguiente resultado, de Gauss, nos dirá que tanto están relacionadas.
R
Teorema 1 Sea jxj < 1 y K(x) = 02 p ds
, entonces
2
2
1 x sen (s)
M (1 + x) =
2K(x)
Demostración Ver [AB]
Esto ya se parece más a lo que queremos llegar. John Landen logra, mediante
una transformación, relacionar ambas ideas y obtiene el siguiente resultado:
1
P
(a)k (b)k k
Teorema 2 Sea F (a; b; c; x) =
, jxj < 1 ,
(c)k k! x
k=0
(m)k = m(m + 1)(m + 2)
(m + k
1) , entonces
L(a; b) = (a + b) F (
1
2;
1
2 ; 1;
2
a b
a+b
)
Haciendo uso del Teorema 2 obtenemos
L(a; b) = (a + b)
= (a + b)
= (a + b)
1
P
1
2 )k (
(
k=0
1
P
k=0
1
P
( 21 )2 (
= (a + b) 1 +
a b
a+b
2
1
2 +1) (
2k
2
1
2 +2)
(k!)2
1 2 1 2 3 2 5 2
2) (2) (2) (2)
(k!)2
(
k=0
"
1
2 )k
(1)k k!
1
4
a b
a+b
2
+
1
P
k=2
(
( 2k2
( 14 )k
1)2
1
2 +k
3 2
)
a b
a+b
a b
a+b
2k
a b
a+b
2k
2k
1
k!
2
k
Y
(2i
i=1
3)2
#
Una buena apriximación depL(a; b) debida a Ekwall y Sipos es:
p
b)4
2(a+b)2 ( a
p
p
p p
4
( a+ b)2 +2 2 a+b ab
L(a; b)
2
2.4.
EJEMPLOS
p
1. Consideremos la elipse con ecuación paramétrica (t) = (2 cos(t); sen(t))
2.4. EJEMPLOS
13
Usando el resultado anterior aproximemos su perímetro.
"
1
2
2k
P
1
2 1
+
( 14 )k 22+11
L(2; 1) = (2 + 1) 1 + 14
2+1
k!
L(2; 1) = 3
k
k
k
k
k
"
2
k=2
1+
=5
L(2; 1)
=9
L(2; 1)
= 15
L(2; 1)
= 50
L(2; 1)
= 100 L(2; 1)
1 2
3
1
4
+
1
P
k=2
( 14 )k
1 2k
3
1 2
k!
k
Y
(2i
(2i
i=1
2
3)
i=1
k
Y
#
3)2
#
9;6884482125373
9;6884482205474
9;6884482205474
9;6884482205474
9;6884482205474
Numericamente nos damos cuenta de la rapidez con la que converge la serie.
Utilizando la aproximación de Ekwall obtenemos: L(2; 1) 9;6884498265932
2. Calcular la longitud de la grá…ca del sen(x) en el intervalo [0; 2 ]:
L(sen(x); 0; 2 ) = 4
Z
=4
=4
=4
2
Z 02
Z
Z
0
2
0
2
p
1 + cos2 (x)dx
p
cos2 (x) + sen2 (x) + cos2 (x)dx
p
sen2 (x) + 2 cos2 (x)dx
q
p
sen2 (x) + ( 2)2 cos2 (x)dx
0
p
notamos que este problema es análogo al ejemplo 1 tomando a = 1 y b = 2
Por lo tanto podemos aproximar esta integral utilizando el método de GaussLanden
p
L(sen(x); 0; 2 ) = L(1; 2)
"
#
k
p
p
Y
1
2
2k
p
P
2
1
1
p 2
= (1+ 2) 1 + 14
+
( 41 )k 1p2+12
(2i 3)2
k!
2+1
k=2
i=1
14CAPÍTULO 2. MÉTODOS NUMÉRICOS PARA APROXIMAR INTEGRALES ELÍPTICAS
k
5
6
7
9
15
500
2,000
1,000,000
L(sen(x); 0; 2 )
7;640395578053309
7;640395578055384
7;640395578055423
7;640395578055423
7;640395578055423
7;640395578055423
7;640395578055423
7;640395578055423
L(sen(x); 0; =2)
1;9100988945133273
1;910098894513846
1;9100988945138557
1;9100988945138557
1;9100988945138557
1;9100988945138557
1;9100988945138557
1;9100988945138557
Capítulo 3
Integrales elípticas en
problemas de la Mecánica,
la Geometría y la Dinamica
de Fluidos.
3.1.
Oscilaciones de un péndulo sin fricción
Consideremos el sistema mecánico que consiste de una masa m, sujeta en un
extremo de una barra rígida e inextensible de longitud L. Suponemos que la
barra es tan delgada que no tiene peso, que está …ja en el otro extremo y que el
sistema oscila de tal manera que el movimiento tiene lugar en un plano.
Si denotamos por (t) el ángulo que forma la barra con la dirección vertical al
tiempo t, la posición de la masa al tiempo t es x(t) = L(sen( (t)); cos( (t)))
15
16CAPÍTULO 3. INTEGRALES ELÍPTICAS EN PROBLEMAS DE LA MECÁNICA, LA GEOMETRÍ
Suponemos que las fuerzas que actúan sobre la masa son su peso y la tensión
de la barra. Esta última es la responsable de que el movimiento de la masa sea
siempre tangencial.
La velocidad de la masa está dada por
x(t) = L (cos( (t)); sen( (t)))
y la aceleración es:
2
x(t) = L (t) ( sen( (t));
cos( (t))) + L (t)(cos( (t)); sen( (t)))
El primer término representa la componente normal de la aceleración, el segundo
términoes la componente tangencial.
El balance de las componentes tangenciales de la fuerza debida al peso y de la
aceleración nos dan la ecuación
+
g
L sen(
(t)) = 0
Este es un sistema conservativo, lo cual es consecuencia de que no estamos
considerando la fricción.
Para obtener la ecuación de conservación de energía, multiplicamos por
integramos entre 0 y t
Rt
0
2
(t)
2
g
L
(s) (s) + (s) Lg sen( (s))ds = 0
2
cos( (t))
(0)
2
En el plano fase de
g
L
+
2
(t)
2
e
cos( (0)) = 0
2
g
(0)
cos( (t)) =
L
2
g
cos( (0)) =: E
L
(4)
y , las curvas integrales del sistema son las grá…cas de
=
p p
2 E+
g
L
cos( (t))
Observe que para cada E, la curva integral correspondiente está de…nida para
E. En la siguiente …gura se
valores de con la propiedad que Lg cos( (t))
muestra una grá…ca del plano fase ; .
3.1. OSCILACIONES DE UN PÉNDULO SIN FRICCIÓN
17
Observando que es periódica de periodo 2 la podemos gra…car en un cilindro
cuya circunferencia sea dicho periodo y obtenemos
Tomando
(0) = a y
(0) = b y sustituyendo en (4) obtenemos
d 2
dt
d
dt
Por lo tanto
dt = p
g
2L
= 2 Lg cos( ) + b2
p
= 2 Lg cos( ) + b2
d
g
cos( )+b2 2 L
cos(a)
=
q
2 Lg cos(a)
2 Lg cos(a)
L q
d
2g
L 2
cos( )+ 2g
b cos(a)
utilizando la identidad trigonométrica cos(x) = 1 2sen2 ( x2 )
q
L q
d
dt = 2g
L 2
1 2sen2 ( =2)+ 2g
b 1+2sen2 (a=2)
q
L q
d
= 2g
L 2
2
2
2sen ( =2)+ 2g b +2sen (a=2)
=
1
2
q
Lq
d
g
L 2
sen2 ( =2)+ 4g
b +sen2 (a=2)
18CAPÍTULO 3. INTEGRALES ELÍPTICAS EN PROBLEMAS DE LA MECÁNICA, LA GEOMETRÍ
Supongamos b = 0 y hagamos el cambio de variable
sen( =2) = sen (a=2) sen( )
cos(
d = 2 p sen(a=2)
2
)d
1 sen (a=2)sen2 ( )
:
Por lo tanto
q
dt =
1
2
dt =
q
=
q
L
g
p
L
g
p
L
g
p
2p
sen(a=2) cos( )d
sen2 (a=2)sen2 ( )
1
sen2 (a=2)sen2 ( =2)+sen2 (a=2)
sen(a=2)
p
=
1 sen2 ( )d
sen2 (a=2)(1 sen2 ( =2))
p
1 sen2 (a=2)sen2 ( )
d
1 sen2 (a=2)sen2 ( )
Sea k 2 = sen2 (a=2), entonces
dt =
s
d
L
p
g 1
(5)
k 2 sen2 ( )
Integrando (5) respecto a t, podemos calcular el periodo del péndulo que denotaremos por T (a):
q R
T (a) = 4 Lg 0 max p
ds
1 k2 sen2 (s)
donde max es el ángulo máximo de apertura del péndulo.
Si k 2 es pequeño (e.d si k 2 = sen2 (a=2) < 1=2), obtenemos una buena aproximación de T (a) por medio de la serie:
i
q h
L
13 2
1 2
2
4
sen
(a=2)
+
::::::
T (a) = 2
sen
(a=2)
+
1
+
2g
2
24
Pero lo que nos interesa es determinar la ecuación de movimiento del péndulo.
Observemos que cuando varía entre 0 y t; varía entre a y ( ) y varía
de max a ( ) . Integrando (5) obtenemos:
Zt
q R
q R
q R
0
p ds
p d2 2 + Lg 0 p d2 2
d = Lg
= Lg
2
2
max
1 k sen (s)
1 k sen ( )
max
0
t=
q R
L
g
max
0
p
d
1 k2 sen2 ( )
t + 14 T (a) =
pg
L (t
q R
L
g
0
+
q R
L
p
g
0
p
d
1 k2 sen2 ( )
ds
1 k2 sen2 (s)
+ 14 T (a)) = F (k; )
1 k sen ( )
3.2. ENCONTRAR EL ÁREA DE LA SUPERFICIE DE LA SECCIÓN SEPARADA DEL CILINDRO X2 +Z2 =A2 PO
F (k; ) =
R
0
p
ds
,
1 k2 sen2 (s)
con k …jo entre cero y uno, es la integral elíptica
incompleta del primer tipo.
Vemos la necesidad de invertir la integral F (k; ) para encontrar la ecuación de
movimiento del péndulo.
La función F (k; ) tiene como inversa la ecuación elíptica de Jacobi denotada
por sn(k; u), la cual estudiaremos con detalle más adelante.
Por ahora nos basta saber que esta función satisface:
u = F (k; ) $ sn(k; u) = sen( )
Por tanto en el caso del péndulo
sen( ) = sn(k;
1
k
pg
sen( 2 ) = sn(k;
L (t
+ 14 T (a)))
pg
L (t
+ 14 T (a)))
Así, la ecuación del movimiento del péndulo queda expresada como
(t) = 2arcsen k sn k;
pg
L (t
+ 14 T (a))
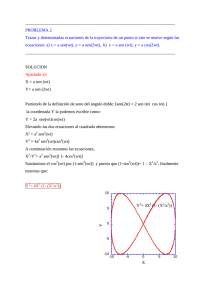
Grá…ca de 2arcsen[ 13 sn( 13 ; u)]
3.2.
Encontrar el área de la super…cie de la sección separada del cilindro x2 +z2 =a2 por el
cilindro x2 +y2 =b2 , donde 0 < b < a
y
z 0
Sea D = f(x; y)jx2 + y 2
b2 ; z
0g y f (x; y) =
p
a2
x2
20CAPÍTULO 3. INTEGRALES ELÍPTICAS EN PROBLEMAS DE LA MECÁNICA, LA GEOMETRÍ
@f
Ya que
=
@x
por:
p
x
a2 x2
ZZ q
1+
A
D
A=
Zb
x2
a2 x2 dxdy
2
p
6
4
p a
a2 x2
b
@f
=0
@y
y
2 x2
bZ
p
b2 x2
Sea s = x=b, entonces
A = 2ab
Zb
=
3
b
el área de la super…cie deseada esta dada
2
p
6
4
p
1 s2
1
2 2
s
( ab )
7
p a
dy 5 dx
a2 x2
b2 x2
7
dy 5 dx = 2a
Z1 r
3
2 x2
bZ
Zb
p
2
2
p b x dx
a2 x2
b
=
Zb p
1
= 2a p
(x=b)2
1 (x=a)2
b
ds = 4ab
1
Z1 r
1 s2
1
2 2
s
( ab )
ds
0
Haciendo el cambio de variable sen( ) = s obtenemos
Z=2 r
Z=2
1 sen2 ( )
cos( )2
q
d =
A = 4ab
cos( )d = 4ab
b 2
2
b 2
1 ( a ) sen ( )
1 (a
) sen2 ( )
0
Z=2
= 4ab
0
Sean k =
b
a
0
q
y
2
1
=
Por lo tanto
A = 4ab
= 4ab
2
( ab )
p
= 1
1
1
k2 (
Z=2
1 sen2 ( )
=
sen2 ( )
d
k 2 sen2 ( ) , entonces
1 k2 sen2 ( ) 1
1
)=
2
+ 4ab
0
Z=2
Z=2
4ab
k2
Z=2
0
p 21 2 d
1 k sen ( )
2
= k sen ( )
sen2 ( ): Sustituyendo en la integral
p k2
1
(
0
p
1
d
1 k2 sen2 ( )
+
0
(
)
1 k2 sen2 ( )
1
)d
d =
dx
3.3. ONDAS VIAJERAS PARA LA ECUACIÓN DE KORTEWEG - DE VRIES21
= 4ab
Z=2
p 21 2 d
1 k sen ( )
+
0
= 4ab 1
4ab
k2
Z=2
0
1
k2
Z=2
p 21 2 d
1 k sen ( )
p
( 1
+
4ab
k2
0
k 2 sen2 ( )
Z=2
0
p
1
p
1
)d
1 k2 sen2 ( )
k 2 sen2 ( )d
Este tipo de integrales se les denomina integrales elípticas del tercer tipo, por
ser una combinación de las de primer y segundo tipos.
3.3.
Ondas viajeras para la ecuación de Korteweg
- de Vries
La ecuación de movimiento para la super…cie de una onda solitaria en agua poca
profuda esta dada por
ut + uxxx + 6uux = 0
(6)
y es llamada la Ecuación de Korteweg-de Vries ya que Korteweg y de Vries la
dedujeron (Ver Apéndice A o [Fl]).
Buscamos soluciones de la forma
u(x; t) = U (x
ct)
con la condición U (n) ( 1) = 0 para n = 0; 1; 2
Sean = x ct y 0 = dd , entonces la ecuación a resolver es
cU 0 + U 000 + 6U U 0 = 0
Integrando (7)con respecto a
obtenemos
cU + U 00 + 3U 2 = 0
Que es un sistema conservativo.ya que
dE
dt
E(t) =
(7)
1 02
2 U (t)
=0
+ U 3 (t)
Por lo tanto
E(t) = E(0)
c 2
2 U (t)
(8)
22CAPÍTULO 3. INTEGRALES ELÍPTICAS EN PROBLEMAS DE LA MECÁNICA, LA GEOMETRÍ
Por lo que las curvas integrales de
U =v
v = cU 3U 2
cumplen que
1 2
2v
+ U3
c 2
2U
= E(0)
o equivalentemente
p
v=
r
c 2
U
2
2
U 3 + E(0)
(9)
que estan de…nidas para
c 2
2U
U3
E(0)
Por lo tanto la grá…ca del potencial '(U ) = U 3 2c U 2 determina la estructura
de las curvas integrales como se muestra en la siguiente …gura
v
P(U)
0.4
0.04
0.2
0.02
0
0
-0.2
-0.2
0
0.2
0.4
0
0.2
0.4
0.6
U
U
-0.2
-0.02
-0.4
'(U ) = U 3
c 2
2U
p pc
2 2U2
v=
U 3 + E(0)
Queremos encontrar soluciones acotadas de (7) con c > 0. En esa dirección
integremos dos veces (7) de 0 a para obtener
1 02
2U
c 2
2U
+ U3
= AU + B
,con: A; B 2 R
Sean U1 < U2 < U3 raíces del polinomio AU + B
dU
d
=
x
U1 )(U
p p
2 (U
U 3 + 2c U 2 , entonces
U2 )(U
U3 )
Por lo tanto el periodo de oscilación esta dado por dos veces T
T =
p1
2
U
R3
U2
Además, si U (0) = U3 obtenemos
p
(U
du
U1 )(U U2 )(U
U3 )
3.3. ONDAS VIAJERAS PARA LA ECUACIÓN DE KORTEWEG - DE VRIES23
p1
2
=
p1
2
=
Sean
s = U3 + (U2
ds = 2(U2
s
U
R3
U
p
RU
U3
p
ds
(s U1 )(s U2 )(s U3 )
du
(s U1 )(s U2 )( s+U3 )
U3 )sen2 ( ) = (U3
U1 + (U2
= (U3
U1 ) 1
k 2 sen2 ( )
s
U2 = (U3
U2 ) 1
sen2 ( ) = (U3
s
U3 = (U2
U3 ) sen2 ( )
q
(U ) = arcsen
U3
h
U1 ) 1 +
U2 U3
2
U3 U1 sen (
i
)
U2 ) cos2 ( )
U U3
U 2 U3
=
=
Por lo cual
U
U3 )sen2 ( )
U3 )sen( ) cos( )d
U1 = U3
Entonces
para U2
p2
2
p
R0
(U )
p
p
2
U3 U1
U 3 U1
(U
R )
0
U ( ) = U2 + (U3
p
p U2
U3 d
1 k2 sen2 ( )(U3 U2 )
d
1 k2 sen2 ( )
U2 )cn2
q
U3 U2
t; k
2
Recordando que = x ct
En el periodo vuelven a aparecer las integrales elípticas y para encontrar U (x
ct) nos volvemos a encontrar con el problema de inversión.
24CAPÍTULO 3. INTEGRALES ELÍPTICAS EN PROBLEMAS DE LA MECÁNICA, LA GEOMETRÍ
Parte II
Funciones Elípticas
25
Capítulo 4
Mapeos del Semiplano
Superior H +
Ejemplos de mapeos de H + en
1) El Primer Cuadrante: f (z) =
La elección del argumento
eje real.
2) Una franja
= fz 2 C j
p
z
3
2; 2
2
A < Re(z) < A
permite calcular la imagen del
y
Im(z) > 0g
Figura 8
Supongamos que f (R) = la frontera orientada de la franja
muestra en la …gura 8)
27
(como se
CAPÍTULO 4. MAPEOS DEL SEMIPLANO SUPERIOR H +
28
Sea (x) = x si x 2 R
y
(x) = f ( (x)) = f (x)
Queremos que la tangente a la imagen dada por (x) = f 0 (x) cambie de
dirección en 90 al cruzar x = 1; 1
p
p
0
2
1 para x 2 R, por lo tanto f (z) = z 2 1
Una
psolución
p es f (z) = x
= z 1 z + 1 para todo z 2 H + . Tomando cortes rama como se
muestra en la siguiente …gura
ya que nos interesa la imagen del eje real y el semiplano superior.
Zz
p
Entonces f (z) =
s2 1ds es un buen candidato.
0
Examinemos algunas propiedades de esta función:
(i) f (0) = 0
(ii) Si
1<s<1
s = 1 + (1
Por lo tanto
p
p
s2 1 = 1
s)ei =
sei
=2
p
1 + (1 + s)ei0 :
p
s + 1ei0 = i 1
s2 :
Entonces
Im(f (fx + i y j x 2 [0; 1] , y = 0g) =
= x + i y j x = 0 , y 2 0;
4
Im(f (fx + i y j x 2 [ 1; 0] , y = 0g) =
= x+i y jy 2
4;0 , x = 0
Si s > 1 entonces s = 1 + (s
f (x) = f (1) +
Zx
p
s2
1)ei0 =
1 + (1 + s)ei0 : Por lo tanto
1ds =
+ r(x)
4i
0
r(x) > 0 ; r(x) ! 1
x!1
29
.
Por lo tanto f (R) queda con orientación negativa y f (H + )
es una franja horizontal.
Para corregir la orientación de f (R) necesitamos
Zz
f (z) =
p ds
s2 1
rotada 90 ,
0
es decir, considerar
Zz
G(z) = i
p ds
s2 1
=
Zz
e
ds
p
i =2
s2 1
0
0
=
Zz
p ds
1 s2
0
La imágen de H + bajo esta función es
fw 2 C j
2
< Re(w) <
Im(w) > 0g:
2
Por lo tanto basta ajustar el ancho de la banda para tener
la función deseada
f (z) =
2A
Zz
p ds :
1 s2
0
3) Un rectángulo
Siguiendo la idea del ejemplo anterior.
Candidato :
f (z) =
Zz
p
ds
p
s2 1 s2 a2
con
a > 1:
0
Los puntos de rami…cación son
argumento es:
2
Entonces para z 2 R , z
f (z) =
Z1
p
s2
ds
p
1 s2 a2
+
0
Sea k =
1
a
j
< 32:
1
Zz
0
< 1, entonces
<
a; 1; 1; a y la elección de las ramas del
p
s2
ds
p
1 s2 a2
= f (1) +
Zz
0
p
ds
p
s2 1 s2 a2
CAPÍTULO 4. MAPEOS DEL SEMIPLANO SUPERIOR H +
30
f (1) =
Z1
p
ds
p
1 s2
=
a2 s2
Z1
1
a
1 s2
ds
p
2
1
s 2
(a
)
=
0
0
=
p
Z1
k
p
1 s2
ds
p
1 2 k 2 s2
=
k F (k; =2 + 2n ) :=
K(k)
0
Así
f (z) =
K(k) +
Zz
p
ds
p
1 s2 a2
s2
=
K(k) +
Zz
Observemos que f(z) tiene puntos de rami…cación en
1 + r2 ei
=
i
= a + r3 e
3
a + r4 ei
=
, r1 = j1
1
2
a; 1; 1 y a: Entonces
sj
, r2 = j1 + sj
, r3 = ja
4
ds
p
s2 1 s2 a2
1
1
z = 1 + ri ei
p
sj
, r4 = ja + sj
2
<
j
<
2
Analicemos la imagen del semiplano superior H + bajo f (z) :
1) Determinar la imagen de [0; a]
a) f (0) = 0 ; f (1) =
K(k)
b) Sea x 2 (0; 1); entonces
p
1
p
s2 1 s2 a2
f (x) =
Zx
p
=
p 1
p 1
e i
1 s2 a2 s2
ds
p
s2 1 s2 a2
=
0
Zx
; por lo tanto
p
ds
p
1 s2 a2 s2
<0
0
) f ([0; 1]) = [0; K(k)]
c) Sea x 2 (1; a), entonces
p
1
p
s2 1 s2 a2
=
p 1
p 1
s2 1 a2 s2
( i) ;
Por lo tanto,
f (x) = f (1)
i
Zx
1
p
s2
ds
p
1 a2 s2
=
K(k)
i
Zx
1
p
ds
p
s2 1 a2 s2
31
En particular
Za
p
f (a) =
s2
ds
p
1 s2 a2
= f (1)
i
p
dx
p
x2 1 a2 x2
=
1
0
=
Za
K(k)
Za
p
1=k
Z
p
i
dx
p
x2 1 a2 x2
=
K(k)
i k
1
Sea K 0 (k) = k
1=k
Z
p
dx
p
x2 1 1 k2 x2
1
dx
p
x2 1 1 k2 x2
, entonces
1
f (a) =
K(k)
i K 0 (k)
Podemos conlcuir
K(k) , y 2 (0; K 0 (k))g
f ([1; a]) = fz = x + iy j x =
f ([0; 1]) = [0; K(k)]
Análogamente
f ([ 1; 0]) = [K(k); 0]
f ([ a; 1]) = f(x; y) j x = K(k); y 2 ( K 0 (k); 0)g
2) Determinar la imagen bajo f de [a; 1]
Sea x > a
y a < s < x , entonces
Zx
ds
p
p
f (x) = f (a) +
= K(k)
s2 1 s2 a2
i K 0 (k) +
a
Notemos que
Zx
p
ds
p
s2 1 s2 a2
a
>0
a
Para determinar f (1) necesitamos calcular
Z1
dx
p
p
I :=
x2 1 x2 a2
a
Haciendo el cambio de variable t = a=x
I=
Z0
1
p
(a=t)2
dx
p
1 (a=t)2 a2
=
1
a
Z0
1
q
1
Zx
dt
p
t2
a2
1 t2
=
p
ds
p
s2 1 s2 a2
CAPÍTULO 4. MAPEOS DEL SEMIPLANO SUPERIOR H +
32
I=k
Z1
p
dt p
1 k2 t2 1 t2
= K(k)
0
Por lo tanto
l m f (x) = l m f (a) +
x!1
x!1
Zx
p
ds
p
s2 1 s2 a2
=
Zx
p
a
= lm
0
K(k)
x!1
iK (k) +
ds
p
s2 1 s2 a2
=
a
=
K(k)
iK 0 (k) + i K 0 (k) =
iK 0 (k)
f ([a; 1]) = fz = x + iy p x 2 ( K(k); 0) ; y =
i K 0 (k)g
Analogamente
f ([ 1; a]) = fz = x + iy p x 2 (0; K(k)) ; y =
i K 0 (k)g
Ahora sabemos que la imágen del eje Real es la frontera del rectángulo con
vértices en
K(k);
K(k)
iK 0 (k); K(k)
iK 0 (k); K(k).
Denotaremos a dicho rectángulo como D:
Más aun, f (z) es analítica y conforme en H + ya que
f
De hecho f es 1
0
(z) =
p
1
p
z 2 1 z 2 a2
6= 0 en H +
1 en H + y suprayectiva en D :
A…rmación f (H + ) = D y para cada w 2 int (D) existe un único z 2 H + tal
que f (z) = w:
Demostración Sea wo 2 Interior de D: Sea
N (wo ) = N umero de soluciones de f (z) = wo con z 2 H +
33
Sea una curva simple cerrada en H + tal que f (z) 6= wo para todo z 2
entonces
R f 0 (z)
N (wo ) = 21 i f (z)
wo dz = Número de soluciones de f (z) =
= wo encerradas por
Tomamos R > a
R
( ) = R ei
,
R
:= [ R; R] +
R
N
(wo ) =
R
1
2 i
Observemos que
f
0
Para estimar
RR
R
2 [0; ]
( )
f 0 (x)
f (x) w dx
R
en
R 2 ei
R
2
1
1
p
R 2 ei
lm
0
2
y sea
R
2
a2
=O
1
R2
y jdzj = R
, demostraremos que
z! 1 , z2H +
Tomemos z = Rei
f 0 (z)
f (z) w dz
R
(Rei ) = p
1
f (z) w
1
2 i
+
1
f (z) =
iK 0 (k)
= t z con t 2 [0; 1] :
Entonces
f (z) = f (R) +
R0
0
p
R 2 ei
2
i
iRe
p
1 R 2 ei
2
a2
ds = f (R) + O( R1 )
Por lo tanto
lm
z! 1 , z2H +
f (z) = l m f (R) =
R! 1
iK 0 (k):
Así 9 Ro > 0 tal que
jf (z) + iK 0 (k)j <
1
2
jwo + iK 0 (k)j para jzj
Ro
,
CAPÍTULO 4. MAPEOS DEL SEMIPLANO SUPERIOR H +
34
como se muestra en la siguiente …gura
Entonces no hay soluciones de f (z) = wo con jzj
jf (z)
jwo + iK 0 (k)j
wo j
Se sigue que para R
Ro pues
1
2
jf (z) + iK 0 (k)j
jwo + iK 0 (k)j
Ro :
R
f 0 (z)
f (z) wo dz
R
R2
=
R
!
R R!1
0
NR (wo ) toma valores en los naturales y tiene límite cuando R ! 1
Por lo tanto 9 R1 tal que N
N
Observemos que
como se muestra
R
R
(w) =
R
:= f (
(wo ) = N
1
2 i
R)
1
R
1
R1
(wo ) 8 R
f 0 (x)
f (x) w dx
para R
R1 y además
R1
es una curva simple orientada positivamente
y si R es tal que wo queda en la región encerrada por
R dv
1
2 i
v wo = 1
R
R
se tiene que
35
entonces
1=
1
2 i
R
dv
v wo
=
1
2 i
R
R
f ’(z)
f (z) w dz
= NR (w);
R
es decir
N (w) = 1 8 w 2 Interior de D
Por lo tanto :
f es 1
1 y f (H + ) = D
f tiene una inversa que denotaremos por sn(z; k) la función
"sinus amplitudinus"de Jacobi:
La función sn(z : k) es analítica en D: Ahora extenderemos por simetría ésta
función a todo el plano.
36
CAPÍTULO 4. MAPEOS DEL SEMIPLANO SUPERIOR H +
Capítulo 5
Sinus Amplitudinus
Sean
D :=
+
= Re‡exión de
=
Re‡exión de
1
=
Re‡
exión de
2
+
con respecto al eje real,
con respecto a la recta Re(z) = K(k)
con respecto a la recta Re(z) = K(k)
Por re‡exión de Schwarz extendemos sn(z; k) por simetría a
z2 +
+
, es decir,. para
sn(z; k) := sn(z; k)
Asi, sn(z; k) es analítica en
[
+
sn(
+
y
; k) = H :
El siguiente paso es extender sn(z; k) a 1 , re‡ejando con respecto a Re(z) =
K(k)
Si z 2 1 , su simétrico respecto a esta recta es z = 2K(k) z, por lo cual
sn(z; k) = sn(z ; k) = sn(2K(k)
z; k)
Es por ésto que después de la re‡exión, con respecto a Re(z) = 3K(k), (donde
z = 6K(k) z) para z 2 3
37
38
CAPÍTULO 5. SINUS AMPLITUDINUS
sn(z; k) = sn(6K(k)
z; k) = sn(2K(k)
Por lo tanto sn(z; k) es analítica en
sn(
1 ; k)
(6K(k)
:=
[
= H ; sn(
+
2 ; k)
z); k) = sn(z
[
1
[
2
4K(k); k):
y
= H +:
Es decir sn(z; k) cumple:
(i) Esta de…nida y es analítica en el rectángulo con vértices en
3K(k) + iK 0 (k); K(k) iK 0 (k) y 3K(k) iK 0 (k):
(ii) sn( iK 0 (k); k) = 1 = sn(2K(k)
K(k)+iK 0 (k);
iK 0 (k); k)
(iii) sn(z; k) = sn(z + 4K(k); k) , sn(z; k) = sn(z + 2iK 0 (k); k) 8 z 2 C:
Es decir, tiene dos periodos independientes y por lo tanto no se puede
expresar en terminos de funciones elementales.
Continuando la extensión por simetría, se obtiene una función meromorfa en el
plano que es doblemente periódica con periodos 4K(k) y 2iK 0 (k):
Podemos pensar a sn(z; k) como una función del toro T 2 = C = (4K(k)Z +
2iK 0 (k)Z) en la esfera S 2 :
Sea el rectángulo con vértices en
y 3K(k):
K(k)+i2K 0 (k); 3K(k)+i2K 0 (k);
= parametrizacion positiva de @
1
2
3
4
Así
=
=
=
=
=
1 (x)
=x
con x 2 [ K(k); 3K(k)]
(x)
=
3K(k)
+ ixK 0 (k)
con x 2 [0; 2]
2
(x)
=
(1
x)3K(k)
xK(k)
+ i2K 0 (k)
con
x 2 [0; 1]
3
0
K(k) + (1 x)(i2K (k)) con x 2 [0; 1]
4 (x) =
1
[
2
[
3
[
4
y
K(k)
5.1. ¿CUÁL ES EL ORDEN DE LOS POLOS DE SN(Z;K)?
R
sn(z; k)dz =
1
R
sn(z; k)dz =
3
3K(k)
R
39
sn(x; k)dx
K(k)
3K(k)
R
sn(x + i2K 0 (k); k)dz =
R
sn(z; k)dz
1
K(k)
Analogamente
R
sn(z; k)dz =
2
Por lo tanto
Z
sn(z; k)dz =
R
sn(z; k)dz
4
4 Z
X
j=1
sn(z; k)dz = 0
(10)
j
Por otra parte
1
2 i
Z
sn(z; k)dz = Res [sn(z; k); z = iK 0 (k)]+Res [sn(z; k); z = 2K(k) + iK 0 (k)]
(11)
De (10) y (11) concluimos
Res [sn(z; k); z = iK 0 (k)] =
Res [sn(z; k); z = 2K(k) + iK 0 (k)]
Es decir, la suma de los residuos en un dominio fundamental es CERO.(resultado
cierto para cualquier función doblemente periódica)
Observación Dado w 2 C la ecuación sn(z; k) = w con w 2
soluciones
Demostración Se tienen las soluciones por construcción
5.1.
tiene dos
¿Cuál es el orden de los polos de sn(z;k)?
Recordemos que
I :=
1
2 i
R
(sn(z;k))0
sn(z;k) w dz
=
= N umero de ceros de (sn(z; k) w) encerrados por
polos de (sn(z; k) w) encerrados por :
N umero de
Ceros y polos contados con multiplicidades. Escogiendo w de tal manera que no
existan soluciones de sn(z; k) = w en : Entonces
I=2
N umero de polos de sn(z; k) encerrados por
40
CAPÍTULO 5. SINUS AMPLITUDINUS
Por otra parte
I=0
ya que el integrando es elíptico y la derivada hereda la periodicidad con lo
mismos periodos de sn(z; k) : 4K(k) y 2iK 0 (k)
Por lo tanto
2 = N umero de polos de sn(z; k) encerrados por
Como sabemos existen 2 polos entonces éstos son simples.
Regresando al problema original:
¿Existe una transformación conforme y 1-1 de H + en un rectángulo
con vértices 0; a; ib y a + ib (a; b > 0) ?
Hemos resuleto el problema para un rectángulo con vértices en
iK 0 (k); K(k)
K(k); K(k)
iK 0 (k); K(k)
mediante la función
f (z; k) =
Zz
p
ds
p
:
s2 1 s2 a2
0
Una solución al problema que nos estamos planteando sería encontrar ko tal que
2K(ko ) = a y K(ko ) = b:
En esa dirección analicemos propiedades de la función K(k) :
1) K(k) es una función creciente de k (con k 2 (0; 1)) ya que
lo es.
2) K((0; 1)) = (0; 1)
l m K(k) = l m k l m
k!0+
k!0+
k!0+
l m K(k) = l m k l m
k!1
k!1
k!1
R1
0
R1
0
p
1 x2
p
dx
p
1 k2 x2
=0
dx
p
1 k2 x2
=1 1=1
1 x2
2
p
1 x2
1
p
1 k2 x2
=0
y como K(k) es creciente 1) entonces K((0; 1)) = (0; 1) :
De 1) y 2) podemos concluir que 2K(k) = a tiene una única solución ko en
(0; 1): Pero para ko …ja K(ko ) = b sólo tiene solución para un valor de b!!!
Por otra parte, queremos que
K(k)
2K
(k) =
o equivalentemente
a
b
5.1. ¿CUÁL ES EL ORDEN DE LOS POLOS DE SN(Z;K)?
K(k)
K (k)
R1
p
0
1=k
R
=
1
x2
1
p
dx
p
k2 x2
1
dx
p
x2
1
1
=
a
2b
41
.
k2 x2
Analicemos la monotonía de las integrales para demostrar que
función creciente de k con imágen (0; 1).
R1
i) Por 1)
0
ii) E(k) :=
p
1 x2
1=k
R
p
1
dx
p
1 k2 x2
p
K(k) = k
0
=
k2 xdx
:
(1 k2 x2 )3=2
! dy =
p
p
p
1
k K(k)
es decreciente. Demostraremos esto comparando
1
k K(k)
1
1 k2 x2
R1
1 x2
dx
p
1 k2 x2
=k
1
p
1
y2 1
pdy
Por lo tanto
1
R k2
1
1
1
R k2
es una
es creciente.
dx
p
x2 1 1 k2 x2
esta integral con
Sea y =
K(k)
K (k)
1 (1 k2 )y 2
yp
dy
ky
p
1 (1 k2 )y 2 ky 2 y 2 1
p
= E( 1
p
=k
1
R k2
1
1
p
y2 1
k2 )
Por lo tanto E(k) es una función decreciente en k ya que:
p
R1
1
dx
p
p
y
1 k 2 son funciones creciente y decreciente
2
2
2
k K(k) =
1 x 1 k x
0
respectivamente en k 2 (0; 1).
Concluimos de i) y ii) que
K(k)
K (k)
es una función creciente en k: Más aun,
A…rmación H ((0; 1)) = (0; 1) con H(k) =
Demostración Por una parte
l m+
R1
k!0 0
p
1
x2
dx
p
1 k2 x2
= lm
R1
k!1 0
K(k)
K (k)
1 x2
qdx
1
Z1
dx
=
2
1 x2
p
2
( k1 )
x2
por convergencia monotona se tiene
lm
Z1
k!1
0
p
1
Por otra parte,
1=k
R
1
p
x2
dx
p
1 1 k2 x2
dx
q
x2 1
=
1
R
0
p
1 2
k
=
x2
dy
p
y 2 +1 y 2 +k2
0
p
con y =
q
1 k2 x2
x2 1
(12)
pdy
1 (1 k2 )y 2
:
42
CAPÍTULO 5. SINUS AMPLITUDINUS
1
y+1
Sea w =
1
R
0
p
entonces
dy
p
y 2 +1
=
y 2 +k2
R1
p
0
w2 +(1 w)2
dw
q
2
( k1 )
w2 +(1 w)2
con k 2 (1; 1)
Pero
p
w2 +(1 w)2
q1
2
( k1 )
p
w2 +(1 w)2
R1
0
1
(1 w)2
1
w2 +(1 w)2 (1 w)
!1
entonces, por convergencia
monotona se tiene que
Z1
dw
q
lm p
k!1
1 2 2
w2 + (1 w)2
w + (1
0
k
Concluimos de (12) y (13) que
0
l m+ H(k) = l m
k!1 1=k
R
k!0
0
Análogamente
R1
p
p
1 x2
qdx
1
w2 +(1 w)2
k!1
K(k)
K (k)
=
b
K (ko )
y h(z) =
2
( k1 )
2
w)
x2
=1
=
=2
=0
1
(13)
(14)
w2 +(1 w)2
1
=1
=2
(15)
es el intervalo (0; 1) para k 2 (0; 1).
Por lo tanto existe ko 2 (0; 1) tal que
Sea
2
( k1 )
dw
q
l m H(k) = 1
Es decir, la imágen de
1
(1 w)2
K(ko )
K (ko )
=
a
2b :
z: Entonces
v(z) := h(sn(z; ko )) +
a
2
+ ib
manda al semiplano superior en el rectangulo con vértices en 0; a; ib; a + ib:
5.2.
¿Cómo ajustar K(k) y K’(k) para tener como dominio un cuadrado, es decir, tal que
K(k)=2K’(k)?
Con el método de la sección anterior, basta tomar a = b. Ahora veremos otra
construcción.
Rz
Sea F (z) = pspdss2 1 ; los cortes rama como antes
0
Determinemos la imágen del eje real bajo F
5.2. ¿CÓMO AJUSTAR K(K) Y K’(K) PARA TENER COMO DOMINIO UN CUADRADO, ES DECIR, TAL QUE K
) Sea z = x 2 (0; 1) , entonces
p
p
s 1 = 1 sei =2
p
p
s+1= s+1
Rx
i pspds1
F (x) =
s2
0
R1
i pspds1
F (1) =
) Para x > 1
;
1 < s < x tenemos
Rx
F (x) =
iA+
1
F (1) =
p pds 2
s 1 s
1
R
iA+
1
Sea t =
B=
1
R
1
1
x
iA
s2
0
p pds 2
s 1 s
1
x2 dx
! dt =
p pds 2
s 1 s
=
R1
0
i A+B
entonces
p pdt
t 1 t2
=A
Procedemos como en caso anterior y concluimos:
a) F (H + ) = Cuadrado con vertices en 0; A;
A
iA y
iA
b) F tiene periodos 2A y 2iA:
c) F tiene una inversa de…nida en ese cuadrado. La extendemos por simetría
y obtenemos una función meromorfa con
) periodos 2A , i2A
) polos en
A
A(1 + i) y en general, en
iA + n2A + im2A = 2(n
1
2 )A
+ 2i(m
1
2 )A
d) Sea
= cuadrado con vertices 0; 2A; i2A; 2A + i2A. La inversa de F
(llamémosla P ) toma cada valor en el plano 2 veces por lo tanto A + iA
es un polo doble con residuo cero.
Por lo tanto esta función es diferente de la que se obtiene con la integral elíptica
de grado cuatro.
Traslademos el cuadrado al cuadrado con vértices en , ; ; (como se muestra en la siguiente …gura).
44
CAPÍTULO 5. SINUS AMPLITUDINUS
Sabemos que P (0) = 0, P 0 (0) = F 01(0) = 0: Por lo tanto el cero es doble. Así
tenemos P y P 0 tienen los mismos periodos y los mismos polos.
5.3.
5.3.1.
Funciones meromorfas con polos y ceros dobles.
¿Qué se puede decir de una función meromorfa g(z)
con polo doble en A + iA y cero doble en cero?
2
z
La función ro (z) = (z (A+iA))
2 cumple con las condiciones de cero y polo de
multiplicidad 2.
Si g es función racional g(z) = p(z)
q(z) (p; q) = 1 y tiene los mismos ceros y polos
que ro (z): Entonces
p(z) = Az 2
y
q(z) = B(z
A
iA)2
Por lo tanto, todas las funciones racionales que satisfacen la condición de ceros
y polos son de la forma
Az 2
B(z A iA)2
5.3.2.
=
A
B
ro (z)
¿Qué otras funciones meromorfas m(z) tienen un
cero doble en 0 y un polo doble en A + iA?
Análisis Local
Tomemos m(z) meromorfa con cero doble en cero y polo doble en A + iA:
Entonces existen 1 (z) analítica en una vecindad del cero que cumple 1 (0) 6= 0
tal que
m(z) = z 2
y
2 (z)
analítica en una jz
(A + iA)j <
1 (z)
que cumple
2 (A + iA)
6= 0 tal que
5.3. FUNCIONES MEROMORFAS CON POLOS Y CEROS DOBLES.
m(z) =
45
2 (z)
(z (A+iA))2
Análisis Global
T (z) = rm(z)
es meromorfa con singularidades en 0 y A + iA . La singularidad
o (z)
en cero es removible ya que
2
1 (z)
T (z) = z z12(z) = (z (A+iA))
2 es analítica en z = 0
(z
(A+iA))2
Por lo tanto T (z) es entera y distinta de cero en todo el plano complejo. Entonces
m(z) = ro (z)H(z)
con H(z) entera y distinta de cero en todo C:
5.3.3.
¿Cuántas funciones elípticas con periodos 2A y 2iA
tienen un cero doble en 0 y un polo doble en A + iA?
Vimos en 5.2 que la función P (z) cumple estas condiciones
Si h(z) es una función elíptica con cero doble en 0, polo doble en A + iA y
periodos 2A y 2iA distinta de P (z) se tiene:
P (z)
(z)
y así Ph(z)
= c 2 C: Es
h(z) es entera y elíptica, por lo tanto acotada en
decir
P (z) = c h(z)
46
CAPÍTULO 5. SINUS AMPLITUDINUS
Capítulo 6
Función P de Weierstrass
¿Cómo construir una función meromorfa con polos en Z + iZ ?
Candidato:
P(z) :=
1
+
z2
X
(n;m)2Z f0g Z f0g
[z
1
(n + im)]2
1
[n + im]2
Convergencia:
Para z …jo se tiene
1
[z (n+im)]2
Si
p
n2 + m2
jz
1
[n+im]2
=
z 2 +2z(n+im)
[z (n+im)]2 [n+im]2
2 jzj
(n + im)j
2
p
n2 + m2
jzj
2
1
2
p
n2 + m2
2
= 14 (n2 + m2 )
Por lo tanto
jzj2
jz (n+im)2 jjn+imj2
4jzj2
(n2 +m2 )2
y como
P
n;m2N
si
p
1
[n2 +m2 ]2
=
n2 + m2 > 2 jzj, entonces
1
P
m=1
P
1
m4
n;m2N
2jzjjn+imj
jz (n+im)2 jjn+imj2
1
P
1
n 2 2
n=1 [1+( m ) ]
1
[n2 +m2 ]3=2
1
P
m=1
1
m3
converge. Además,
8jzj
p
(n2 +m2 ) n2 +m2
47
c
=
8jzj
(n2 +m2 )3=2
(16)
48
CAPÍTULO 6. FUNCIÓN P DE WEIERSTRASS
Se sigue que la serie converge uniforme y absolutamente en subconjuntos compactos de C (Z + iZ):
Así nuestro candidato es una función meromorfa con polos dobles en Z + iZ.
A P(z) le llamamos la función P de Weierstrass.
¿Qué relación hay entre la función P de Weierstrass y P (z) la inversa
Rz
de pspds1 s2 ?
0
6.1.
Ecuación Diferencial para P (z)
Sea F (z) =
Rz
0
p pds 2
s 1 s
entonces z = F (P (z)) =
PR(z)
0
1= p
P 0 (z)
P (z)
p
1 P (z)2
p pds 2
s 1 s
, por lo cual
ó
2
(P 0 (z))
P (z)
=
P (z)2
2
2
1
(17)
Tenemos que, para t real; P (t) es una solución real y periódica del sistema conservativo
::
x
3 2
2x
+x=0
(Ecuación similar a las ondas viajeras para KdV)
Es decir, este sistema mecánico tiene soluciones periódicas dadas por
P (t); t 2 R
6.2.
Ecuación Diferencial para P
La función
P 0 (z) =
2
Z3
+
P
(n;m)2Z f0gxZ f0g
2
[z (n+im)]3
es elíptica con polos en n + im 2 Z + iZ y periodos i y 1:
Sean
P
1
1
S1 (z) =
[z (n+im)]2
[n+im]2
(n;m)2Z f0gxZ f0g
S2 (z) =
P
(n;m)2Z f0gxZ f0g
Entonces
P 0 (z) = Z 32
2S2 (z)
1
[z (n+im)]3
6.2. ECUACIÓN DIFERENCIAL PARA P
1
z2
P(z) =
+ S1 (z)
2
4
P (z) = z6 + z83 S2 (z) + 4 (S2 (z))
2
P(z)3 = z16 + z34 S1 (z) + z32 (S1 (z)) +
P 0 (z)2 4P(z)3 = 4S2 (z)2 + z83 S2 (z)
0
49
2
3
(S1 (z))
12
z 4 S1 (z)
12
2
z 2 S1 (z)
4S1 (z)3
Por otra parte
0
000
2
00
3
S1 (z) = S1 (0) + S1 (0) z + S1 (0) z2! + S1 (0) z3! +
S1 (0) = 0
P
0
S1 (0) = 2!
(n;m)2Z f0gxZ f0g
P
00
S1 (0) = 3!
1
(n+im)3
(n;m)2Z f0gxZ f0g
000
S1 (0) =
1
(n+im)4
P
4!
(n;m)2Z f0gxZ f0g
(2j+1)
Observamos que S1
=0
1
(n+im)5
=0
(0) = 0
Más aun
P
(j)
S1 (0) =
(n;m)2Z f0gxZ f0g
P
=
(n;m)2Z f0gxZ f0g
1
(n+im)j
=
1
(n+im)j
P
(n;m)2Z f0gxZ f0g
Concluimos así
(j)
S1 (0) 2 R 8j 2 N [ f0g
S1 (z) = S1 (z)
P(z) =
1
z2
+ S1 (z) =
Analogamente
S2 (0) = 0
0
S2 (0) = 3
00
S2 (0) = 0
1
z2
+ S1 (z) =
P
(n;m)2Z f0gxZ f0g
(2l)
S2 (0) = 0 8l 2 N
Así mismo:
(l)
S2 (0) 2 R 8l 2 N [ f0g
S2 (z) = S2 (z)
P 0 (z) = P 0 (z)
1
(n+im)4
1
z2
+ S1 (z) = P(z)
1
(n im)j
=
50
CAPÍTULO 6. FUNCIÓN P DE WEIERSTRASS
Por lo tanto la parte singular de P 0 (z)2
g2
1
z2
con
g2 =
4P(z)3 en z = 0 es de orden
!
P
1
60
(n+im)4
1
z2
y es:
(n;m)2Z f0gxZ f0g
Entonces
P 0 (z)2
4P(z)3 =
g2
z2
+ h(z)
con h(z) analítica en z = 0
P 0 (z)2
4P(z)3 + g2 P(z) = h1 (z)
con h1 analítica en z = 0
Pero P 0 (z)2 4P(z)3 +g2 P(z) es elíptica, por lo tanto constante. Dicha constante
es
P
1
g3 = 140
(n+im)6
(n;m)2Z f0gxZ f0g
Es decir
P 0 (z)2
4P(z)3 + g2 P(z) =
g3 :
Por lo tanto
2
3
(P 0 (z)) = 4 (P(z))
g2 P(z)
g3 = 4 (P
e1 ) (P
e2 ) (P
e3 )
(18)
Esta función también da soluciones periódicas de un sistema conservativo similar
al de las ondas viajeras para KdV
De (17) y (18) demostraremos que
con PA (z) =
1
Z2
+
P (z) = cPA (z + (A + iA))
P
1
(n;m)2Z f0gxZ f0g
[z (2nA+i2Am)]2
(19)
1
[2An+i2Am]2 :
Esta relación saldra de la función T HET A principalmente.
Capítulo 7
Función Theta
7.1.
Ecuación de Calor
Para resolver la ecuación en derivadas parciales
ut = uxx
en [0; ]
con condiciones de frontera periódicas
u(0; t) = u( ; t)
,
u(x; o) = f (x)
Se construye la solución fundamental, que corresponde a
u(x; 0) =
o (x)
,
o
es la delta de Dirac en x = 0
Para
1
P
u(x; 0) = f (x) =
fn ei2nx
n= 1
la solución queda de la siguiente forma:
1
P
u(x; t) =
cn (t) ei2nx
n= 1
cn (t) =
4n2 cn (t)
cn (t) = fn e
cn (0) = fn
4n2 t
como en nuestro caso f = 0 tenemos que fn = 1
Entonces la solución fundamental es
1
P
e
4n2 t
n= 1
51
ei2nx
52
CAPÍTULO 7. FUNCIÓN THETA
que converge 8 t > 0 y x 2 R (z 2 C)
Por este tipo de expresiones aparece la función T HET A:
Para cada
2 H + se cumple ei
1 y por lo tanto 9t 2 R tal que
ei
=e
4t
con
z 2 C y Im ( ) > 0 .
Consideremos la serie
1
P
ein
2
einz
n= 1
A esta serie la llamaremos la función T HET A
(z p q) =
1
P
qn
2
ei2nz
q = ei
;
n= 1
La serie converge absoluta y uniformemente para z 2 K con K
pues
Im( )
jqj = e
C compacto
<1
Por lo tanto (z p q) es entera.
Por otra parte
(z +
p q) = (z p q)
8z2C
entonces no tiene un segundo periodo independiente, ya que de tenerlo, por ser
entera sería constante.
Aun así podemos econtrar relaciones interesantes entre (z +
p q) y (z p q),
veamos
1
1
P
P
2
2
(z +
p q) =
q n ei2n(z+ ) =
q n ei2n
ei2nz =
n= 1
=
1
P
n= 1
qn
2
+2n
ei2nz = q
1
e
i2z
n= 1
=q
1
1
P
q (n+1)
2
ei(n+1)2z =
n= 1
e
i2z
(z p q)
A
se le llama un cuasiperiodo y decimos que (z p q) es cuasi-doblemente
periódica con factor de periodicidad o multiplicador: q 1 e i2z :
De…nimos
4
(z p q) =
par de z
3
(z p q) =
1
P
( 1)n q n
2
ei2nz = 1 + 2
n= 1
4
z+
1
P
( 1)n q n
2
cos(2nz) función
n=1
2
pq =
1
P
2
q n ei2nz = 1 + 2
n= 1
1
P
n=1
qn
2
cos(2nz)
7.2. PROPIEDADES DE LAS FUNCIONES T HET A
1
(z p q) =
=
iei(z+
iei(z+
)
4
4
z+
4
1
P
)
53
pq =
4
( 1)n q n
2
ein
ei2nz =
n= 1
=
=
iei(z+
4
( 1)n q (n+1=2)
n= 1
=
( 1)n q n
2
+n
ein
ei2nz =
n= 1
1
P
i
1
P
)
i q 1=4 eiz + 2
1
P
2
ei(2n+1)z =
( 1)n q (n+1=2)
2
sen((2n + 1)z)
n=0
2
(z p q) =
Las funciones
Cada
j
z+
1
1; 2; 3
pq =2
2
y
1;
2
sen((2n + 1)z)
2 H+
es función periódica de z con periodo , es decir
tiene cuasiperiodo
2 y
3:
4
q (n+1=2)
n=0
son enteras para cada
4
j
4
1
P
(z +
p q) =
(z +
p q) =
j
(z p q)
y factor de periodicidad
1
P
( 1)n q n
2
ei2nz ei2n
q
1
2
ei2(n+1)z =
e
i2z
, que heredan
=
n= 1
=q
1
P
1
( 1)n q (n+1)
2
ei2nz =
n= 1
=
q
1
e
i2z
1
P
( 1)n+1 q (n+1)
n= 1
=
Observación Si
q
1
j (zo ; q)
e
i2z
4
(z p q) :
= 0 entonces
j (zo
+k
; q) = 0 8k 2 Z
Demostración Inmediata del comentario anterior.
7.2.
Propiedades de las funciones T HET A
Sea Q el paralelogramo con vértices en a; a + ; a +
y a + + , de
tal forma que 4 (z; q) 6= 0 para z 2 @Q.
¿Cuántos ceros tiene 4 en Q?
Por el principio del argumento tenemos que el número de ceros buscados esta
dado por
1
2 i
R
@Q
0
j (z;q)
j (z;q)
Una parametrización de @Q esta dada por:
dz
54
CAPÍTULO 7. FUNCIÓN THETA
f igura2
1 (t)
=a+t
2 (t)
1
3
1
4
=a+
+t
(t) =
1 (t)
(t) =
2 (t)
+
Entonces
R
0
4 (z;q)
4 (z;q)
dz =
R
0
4 (z+
;q)
;q) dz
4 (z+
1
3
Por otra parte derivando
0
4
(z +
p q) =
d
dz 4
(z +
p q) =
1
q
e
0
4
i2z
(z p q)+2iq
1
e
i2z
4
(z p q)
Por lo tanto
0
4 (z+
4 (z+
pq)
pq)
q
q
=
1
1
i2z
e
e
i2z
0
4 (zpq)
4 (zpq)
+
2iq
q
1
e
e
1
i2z
4 (zpq)
i2z
4 (zpq)
Regresando a la integral anterior obtenemos
R
0
4 (z;q)
dz
4 (z;q)
=
3
R
0
4 (z;q)
dz
4 (z;q)
1
R
+ 2i dz =
1
R
0
4 (z;q)
4 (z;q)
dz + 2i
1
y por periodicidad tenemos que
R
0
4 (z;q)
2+ 4
4 (z;q)
dz = 0
Por lo tanto
1
2 i
R
@Q
0
4 (z;q)
4 (z;q)
dz =
1
2 i
"
R
1
0
4 (z;q)
4 (z;q)
dz +
R
2+ 4
0
4 (z;q)
4 (z;q)
dz +
R
3
0
4 (z;q)
4 (z;q)
#
dz = 1:
7.2. PROPIEDADES DE LAS FUNCIONES T HET A
55
Es decir, 4 (z) tiene exactamente un cero en Q y dicho cero, que denotaremos
por zo ,es simple porque la integral lo cuenta con multiplicidad (El análisis es
análogo para 1 ; 2 ; 3 se deja como ejercicio para el lector.).
Recordemos que si f es una función elíptica con periodos 2w1 ; 2w2 ; Q un
paralelogramo fundamental con vértices en a; a + 2w1 ; a + 2w2 y a + 2w1 + 2w2
con a tal que f no contenga ceros ni polos en @Q entonces
R
@Q
f 0 (z)
f (z) dz
= 0:
Otra manifestación de que las funciones j no son doblemente periódicas.
(Por periodicidad y por principio del argumento el número de ceros de f en Q
es igual al número de polos de f en Q)
56
CAPÍTULO 7. FUNCIÓN THETA
Capítulo 8
Hacia el problema de
inversión
Dados dos periodos independientes ¿Existe una función elíptica con
esos periodo, polos y ceros especi…cados?
En general no siempre podremos construir funciones elípticas con condiciones
arbitrarias. Ésto es debido al siguiente resultado.
Teorema 8.0 Si f es una función analítica con periodos 2w1 , 2w2 y Q es un
paralelogramo fundamental en los que a1 ; :::; an y b1 ; :::; bn son los ceros y polos
entonces
n
P
n
P
aj
j=1
j=1
bj = k 2w1 + l 2w2 con k; l 2 Z .
n
Demostración Sea f una función meromorfa con ceros en faj gj=1 y polos en
n
fbj gj=1 posiblemente repetidos (dependiendo de multiplicidad) en una región
Q. Entonces, por la fórmula integral de Cauchy
R
z
@Q
f 0 (z)
f (z) dz
=
n
P
ai
i=1
n
P
bi
i=1
Si f es elíptica de periodos 2w1 y 2w2 ¿Cuánto vale
R
0
(z)
z ff (z)
dz?
@Q
Sean
R
z
1;
2;
f 0 (z)
f (z) dz
3
Sea
y
3
=
4
R
como en f igura2:
(z + 2w2 )
f 0 (z+2w2 )
f (z+2w2 ) dz
1
1 (t)
= f(
1 (t)),
=
R
z
f 0 (z)
f (z) dz
2w2
1
entonces 1 es una curva cerrada, por lo cual
R
R
0
(z)
z ff (z)
dz = dw
w = 2 i
1
1
57
R
1
f 0 (z)
f (z) dz
58
CAPÍTULO 8. HACIA EL PROBLEMA DE INVERSIÓN
Analogamente para 2 y
n
n
R
P
P
ai
bi = 21 i z
i=1
i=1
4 :Por
0
lo tanto "
f (z)
f (z) dz
@Q
1
2 i
=
2w2
1
R
f 0 (z)
f (z) dz
2w1
R
f 0 (z)
f (z) dz
2
#
=
= 2w2 k + 2w1 l
8.1.
Funciones Elípticas de Grado 1
De…nición.Una función elíptica que tiene un cero simple y un polo simple en
Q (paralelogramo fundamental) se dice que tiene grado 1.
Problema Dados a1 , b1 en Q. ¿Podemos construir una función elíptica con
periodos
y
, cero simple en a1 , polo simple en b1 ?
Candidato:
'(z) =
4 (z
a1 +zo ;q)
b1 +zo ;q)
4 (z
Para que este candidato sea el bueno tiene que ser una función periódica de
periodo : Calculemos.
'(z +
)=
q
q
1
1
e
e
i2(z
a1 +zo )
4 (z
i2(z
b1 +zo )
4 (z
Por lo tanto ' es elíptica si y sólo si b1
Entonces
'(z) =
a1 +zo pq)
b1 +zo pq)
a1 = m
4 (z
4 (z
=e
a1 +zo ;q)
a1 m +zo ;q)
i2(b1 a1 )
'(z)
para algún entero m .
= 1:
Así, '(z) es trivial. Si f es elíptica de grado 1, entonces 9 un único b1 polo
simple de f . Por lo tanto
f (z) =
R1
z b1
+
1
P
an (z
n
bn )
n=0
y por periodicidad se tiene
R1 =
1
2 i
R
f (z)dz =
1
2 i
R
f (z)dz = 0
@Q
Entonces b1 es singularidad removible !!! Por lo tanto f es analítica y por tanto
constante.
Así se tiene el siguiente resultado
Teorema 8.1 Las únicas funciones elípticas de grado 1 son las funciones constantes.
8.2. FUNCIONES ELÍPTICAS DE GRADO 2
8.2.
59
Funciones Elípticas de Grado 2
Ahora buscamos funciones elípticas con ceros en a1 , a2 y polos en b1 , b2 en Q
(paralelogramo fundamental determinado por los periodos).
Candidato a función elíptica con periodos
y :
(z) =
4 (z
4 (z
a1 +zo ;q)
b1 +zo ;q)
4 (z
4 (z
a2 +zo ;q)
b2 +zo ;q)
Procedemos como en el caso de las de grado 1 y concluimos que (z) cumple la
condición de los periodos si y sólo si
b1 + b 2
(a1 + a2 ) = m
y b 1 + b2
(a1 + a2 ) = l
para m; l 2 Z .
Por lo tanto es elíptica con periodos
y
pero están condicionados los
ceros y polos, así que no siempre va a ser la que buscamos.
Dados periodos 2w1 , 2w2 y a1 ,a2 ,b1 ,b2 2 Q tales que
a1 + a2
(b1 + b2 ) = k 2w1 + l 2w2 y
w1
w2
2 H+
podemos construir una función elíptica con periodos 2w1 , 2w2 ceros en a1 ; a2 ;
polos en b1 ; b2 : A saber la función
M (z) =
z a1
4 ( 2w
1
z b1
4 ( 2w
1
+zo ;q)
+zo ;q)
Para la periodicidad en 2w2 tomemos
=
z a2
4 ( 2w
1
z b2
4 ( 2w
1
w1
w2
+zo ;q)
+zo ;q)
y ajustemos.
Ejemplo: La función sinus amplitudinus de Jacobi es una función elíptica de
grado 2.
Sea Q el rectángulo con vértices en
1
2 K(k)
i 12 K 0 (k);
1
3 0
7
2 K(k) + i 2 K (k); 2 K(k)
i 21 K 0 (k); 72 K(k)
i 32 K 0 (k).
Entonces
a1 = 0 , a2 = 2K(k) , b1 = i K 0 (k) , b2 = 2K(k) + iK 0 (k):
Por lo tanto
b 1 + b2
Como queremos
(a1 + a2 ) = 2K(k) + 2iK 0 (k) 2K(k) = 2iK 0 (k) =
=0
+1
i 2 K 0 (k):
2 H + tomamos
b 1 + b2
con m = 0 y l = 1:
Por otra parta, la función
= i 2 K 0 (k): Entonces
(a1 + a2 ) = m
+l
60
CAPÍTULO 8. HACIA EL PROBLEMA DE INVERSIÓN
(z) =
z
4 ( 4K(k) +zo ;q)
z iK 0 (k)
(
+zo ;q)
4
4K(k)
2K(k)
+zo ;q)
4K(k)
(2K(k)+iK 0 (k))
+zo ;q)
4K(k)
4(
4(
z
z
tiene ceros simples en 0 y 2K(k) ; polos simples en i K 0 (k) y 2K(k) + iK 0 (k)
y periodos 4K(k) e i2K 0 (k).
Tomando = i 2 K 0 (k) se tiene que
constante. Así,
sn(z; k) = p
z
4 ( 4K(k) +zo ;q)
z iK 0 (k)
+zo ;q)
4 ( 4K(k)
(z)
sn(z;k) es
elíptica y entera, por lo tanto
z 2K(k)
+zo ;q)
4K(k)
(2K(k)+iK 0 (k))
+zo ;q)
4K(k)
4(
4(
z
para algún p 2 C:
De este ejemplo vemos que podemos escribir la función sn(z; k) en términos de
la función T HET A
8.3.
Función P de Weierstrass
En el ejemplo anterior escribimos la función sn(z; k) en términos de la función
T HET A Veamos si podemos escribir a la función P de Weierstrass en términos
de la función T HET A:
La función P de Weierstrass dada por
P
1
1
P(z) = z12 +
[z (n+im)]2
[n+im]2
(n;m)2Z f0g Z f0g
es meromorfa con polos dobles en Z + iZ, elíptica con periodos i , 1 y solución
de la ecuación diferencial
2
3
[P 0 (z)] = 4 [P(z)]
g2 =
60
P
g2 P(z)
(n;m)2Z f0g Z f0g
g3 = 140
g3
1
(n+im)4
P
(n;m)2Z f0g Z f0g
1
(n+im)6
Consideremos el cuadrado Q con vértices en: 12 + 2i , 12 + 2i , 21 2i y 12 2i :
Si no hay ceros en @Q entonces P(z) = 0 tiene dos soluciones en el interior de
Q:
Observaciones
(I) P(z) es una función par y P 0 (z) es una función impar
(II) Sean e1 , e2 y e3 raíces del polinomio w3
P( 21 ) = e1 , P( 2i ) = e2 , P( 12 + 2i ) = e3 :
(III) g3 = 0
g2
4 w
g3
4 ,entonces
8.3. FUNCIÓN P DE WEIERSTRASS
61
Demostración.
(I) Claro
(II) Si zj 2 C es tal que P(zj ) = ej entonces por (17), P 0 (zj ) = 0
De (I) P 0 ( 21 ) =
P 0(
1
2)
P 0(
=
1
2
+ 1) =
P 0 ( 21 ) , entonces
P 0 ( 12 ) = 0
Análogamente
P 0 ( 2i ) = 0 = P 0 ( 12 + 2i )
Combinando este último resultado con (17) tenemos que para c 2
3
g2
4
[P(c)]
g3
4
P(c)
=0
Es decir,
P(c) es raíz del polinomio w3
g2
4 w
g3
4
Por de…nición de e1 , e2 y e3 se tiene el resultado.
(III) De (II)
g2
4 w
w3
g3
4
= (w
P( 12 ))(w
P( 2i ))(w
P( 12 + 2i )).
Igualando coe…cientes se tienen las siguientes relaciones
a) P( 12 ) + P( 2i ) + P( 12 + 2i ) = 0
b) P( 21 )P( 2i ) + P( 12 )P( 12 + 2i ) + P( 2i )P( 12 + 2i ) =
g2
4
c) P( 12 )P( 2i )P( 12 + 2i ) = g3
Desarrollando a) obtenemos
0 = P( 21 ) + P( 2i ) + P( 12 + 2i )
"
P
1
= 4+
[(n 1 )+im)]2
+
"
(n;m)2Z f0gxZ f0g
4
2
P
(n;m)2Z f0gxZ f0g
Por lo tanto
P( 12 + 2i ) = 0
Sustituyendo en c) obtenemos
g3 = 0
[(m
1
[n+im]2
1
1
2
2 ) in]
#
+
1
[m in]2
#
+ P( 12 + 2i )
1 i 1
2; 2; 2
+
i
2
62
CAPÍTULO 8. HACIA EL PROBLEMA DE INVERSIÓN
Tomemos como cuadrado fundamental Q el cuadrado con vértices en:
3
4
+ i 34 ;
1
4
+ i 43 ;
1
4
i
4
;
3
4
i
4
en donde 0 y 12 + 2i forman un conjunto irreducible de ceros y polos, ambos
dobles.
Por lo cual, tomando = i
4
P(z) =
( (z [ 12 + 2i ])+zo )
2
,
4 ( z+zo )
2C
Ya vimos que podemos expresar las funciónes elípticas de Jacobi en términos
de la función T HET A: También la función P de Weierstrass.
¿Podremos expresar las funciones elípticas en términos de la función
P de Weierstrass?
Sea f una función elíptica de grado 2 que cumple las siguentes condiciones:
a) Periodos 1 e i
b) Ceros a1 y a2
c) Polos en b1 y b2 ambos distintos de cero
d) f es par.
e) a1 + a2 y b1 + b2 no son periodos
Entonces f 0 es impar, por lo cual
f 0 ( 21 ) = f 0 ( 2i ) = f 0 ( 12 + 2i ) = 0:
Los ceros a1 y a2 son distintos ya que si fueran el mismo sería un cero de f 0 :Más
aun
fa1 ; a2 g \
1 i 1
2; 2; 2
i
2
+
=
Por lo tanto f 0 (ai ) 6= 0 para i 2 f1; 2g. Entonces
[P(z)
P(a1 )] y [P(z)
P(a2 )]
tienen cero simple en z = a1 y z = a2 respectivamente.
Analogamente se tiene que
fb1 ; b2 g \
1 i 1
2; 2; 2
+
i
2
=
ya que si fuera distinto del vacío subiría el grado de la función. Entonces
[P(z)
P(b1 )] y [P(z)
P(b2 )]
8.3. FUNCIÓN P DE WEIERSTRASS
63
tienen cero simple en z = b1 y z = b2 respectivamente.
Por lo tanto
f (z) =
[P(z)
[P(z)
P(a1 )] [P(z)
P(b1 )] [P(z)
P(a2 )]
;
P(b2 )]
2C
(20)
En el caso general, se considera
f (z) =
1
2
[f (z) + f ( z)] +
1 f (z) f ( z) 0
P (z):
2
P 0 (z)
Por lo tanto las funciones P(z) y P 0 (z) son base para el espacio de f unciones
el{pticas con periodos 1 e i:
Ésto se generaliza a periodos 2w1 y 2w2 , de la serie (2) que de…ne a la función
P cambiando z (n + im) por z (n2w1 + m2w2 ). Ver [WW]
64
CAPÍTULO 8. HACIA EL PROBLEMA DE INVERSIÓN
Apéndice A
Korteweg-de Vries
El descubrimiento de las ondas solitarias en aguas poco profundas lo hizo el
ingeniero inglés Scott Russell, en el Canal de Edinburgo a Glasgow en el año de
1834. Sus observaciones las reportó a la British Association for the Advancement
of Science en 1844. A la estructura bien de…nida y localizada, objeto de ese
reporte, la bautizó como "la gran onda de traslación". A continuación citamos
un párrafo.
"Observaba el movimiento de un bote jalado por dos caballos en una parte
angosta del Canal, cuando el bote se detuvo súbitamente, no así la masa de
agua que se había puesto en movimiento. Ésta se acumuló alrededor de la proa
del bote y se movió hacia adelante con la forma de una larga elevación solitaria.
La seguí a caballo. La elevación de agua, que era de unos 10 metros de largo y 50
centímetros de alto, continuó su curso por el canal, aparentemente sin cambio
de forma o disminución en su velocidad, que era de unos 15 kilómetros por hora.
Su altura disminuyó después de tres kilómetros."
Russel realizó experimentos en su laboratorio, generando ondas solitarias al
dejar caer un objeto pesado en un extremo de un estanque angosto.
Dedujo empíricamente que el volumen de agua en la onda es igual al volumen
desplazado y que la velocidad de la onda solitaria es: c2 = g(h + a), g es la aceleración debida a la gravedad, a es la amplitud de la onda y h es la profundidad
en reposo.
Para fundamentar estos resultados, Boussinesq (1871) y Rayleigh (1876) supusieron que la longitud de la onda es mucho mayor que la profundidad. A
partir de las ecuaciones de movimiento para un ‡uido no viscoso e incompresible, dedujeron la fórmula de Russell para la velocidad. También encontraron
que el per…l de la super…cie del agua es:
1
4h2 (h + a), en el caso ha
1:
(x; t) = a sec h2 [b(x ct)] , con b 2 = 3a
La contribución de Korteweg y de Vries en 1895 fue la deducción de la ecuación
de movimiento para la super…cie.
A continuación presentamos una deducción de la ecuación de Korteweg y de
Vries a partir de las ecuaciones de Euler para un ‡uido incompresible, en el caso
h
1:
65
66
APÉNDICE A. KORTEWEG-DE VRIES
Consideremos un elemento de volumen V encerrado por S @V:
(x1 ; x2 ; x3 ) y t denotan la posición y el tiempo. !
u ; y p denotan la velocidad,
densidad y presión del ‡uido, respectivamente.
!
n es la normal unitaria a S:
La masa de ‡uido contenida en V al tiempo t es:
ZZZ
m(t) =
( ; t)d
Como la región V no cambia en el tiempo, la tasa de cambio de la masa con
respecto al tiempo es
ZZZ
@
dm
dt =
@t d
La ley de conservación de masa garantiza que el cambio en la masa se debe
únicamente al ‡ujo neto de masa a través de la frontera, es decir,
ZZ
dm
(!
u;!
n )d
dt =
S
Del Teorema de la divergencia se sigue que
@
@t
+ div( !
u)=0
en la región ocupada por el ‡uido, ya que su integral sobre cualquier parte de
esa región es cero.
De manera análoga se obtiene la ecuación de balance para el momento lineal. La
densidad de momento en la i esima dirección es ui : El cambio en el momento
viene de tres factores: el ‡ujo neto de momento a través de la frontera, las
ferzas super…ciales y las fuerzas volumétricas. En nuestro caso, éstas últimas son
debido a la gravedad y actúan en la dirección vertical. La ecuación de balance
de momento es:
ZZZ
ZZ
ZZ
ZZZ
@( ui )
!
!
d
=
u
;
n
)d
+
pn
d
+
Fi d
u
(
i
i
@t
S
S
Procediendo como antes obtenemos las ecuaciones
@( ui )
@t
+ div( ui !
u)+
@p
@xi
Fi = 0
En el caso del agua la densidad es constante, por lo cual la ecuación de conservación de masa es
div(!
u)=0
Las ecuaciones de conservación de momento son
67
@ ui
@t
+
3
P
@(ui uj )
@xj
j=1
1 @p
@xi
=
+ Fi
para i = 1; 2; 3: O en forma vectorial
@!
u
@t
+ (!
u r) !
u =
1
rp
!
gk
Tomando rotacional en la ecuación de momento obtenemos para !
w =r !
u una
ecuación diferencial parcial lineal de primer orden que garantiza que !
w ( ; t) 0
para t > 0 si esta condición se cumple para t = 0. En este caso hay un potencial
de velocidades de tal forma que !
u = r . La ecuación de conservación de
masa es ahora la ecuación de Laplace para el potencial de velocidades: 4 = 0.
@u
@
@xi
2
@
@xj
@
Usando que uj @xji = 12 u @x
i
@
@t
+
, obtenemos la ecuación de Bernoulli
1
2
2
jr j + 1 p + gx3 = 0
Como podemos absorber cualquier función de t en el potencial, se sigue que
@
@t
+
1
2
2
1
jr j +
(p
po ) + gx3 = 0
Esta ecuación determina a la presión una vez que conocemos el potencial de
velocidades. Para determinar el potencial necesitamos condiciones de frontera.
En la super…cie del fondo se debe tener que la componente normal de la velocidad
@
sea cero, es decir @x
= (x1 ; x2 ; 0; t) = 0 para (x1 ; x2 ) en la región que forma la
3
base del volumen ocupado por el ‡uido y para todo t > 0.
En la super…cie libre tenemos dos condiciones acopladas: la velocidad normal
de la super…cie debe coincidir con la velocidad normal del ‡uido y la presión en
el agua debe coincidir con la presión en el aire.
La super…cie libre es de la forma (t) = f : f ( ; t) = 0g :
Si (t + 4t) se ha separado de (t) una distancia 4s en o en la dirección
normal, es decir, f ( o ; t) = 0 y f ( o + 4s!
n ; t + 4t) = 0, entonces
f(
o
+ 4s!
n ; t + 4t)
f(
o; t
+ 4t)+ f (
o; t
+ 4t)
f(
o ; t)
=0
Usando el Teorema del Valor Medio, dividiendo por 4t y tomando el límite
cuando esta cantidad tiende a 0 obtenemos
ds
dt
=
1 @f
jrf j @t
Por otra parte, la componente normal de la velocidad es
!
u !
n =
1
jrf j r
rf
Por lo tanto, r rf = @f
@t :
Supondremos que no hay rompimiento de olas y por lo tanto la super…cie libre
es la grá…ca de una función de x1 ; x2 y t, es decir
68
APÉNDICE A. KORTEWEG-DE VRIES
f ( ; t) = x3
(x1 ; x2 ; t)
h
Usando la identidad del párrafo anterior encontramos la ecuación para la super…cie del agua:
@
@t
@
@
@x1 @x1
+
+
@
@
@x2 @x2
=
@
@x3
Ahora usamos que los cambios en la presión del aire son pequeños para tomar
p = po en la super…cie x3 = h + (x1 ; x2 ; t), lo cual da
@
@t
+
1
2
2
jr j + g = 0
La región ocupada por el ‡uido es f(x1 ; x2 ; x3 ) p 0
el problema completo es
(A )
x3
h + (x1 ; x2 ; t)g y
i) 4 = 0 en 0 < x3 < h + (x1 ; x2 ; t)
ii)
@
@x3 (x1 ; x2 ; 0; t)
=0
para todo t
0
2
iii)
@
@t
+
1
2
iv)
@
@t
+
@
@
@x1 @x1
jr j + g = 0 en x3 = h + (x1 ; x2 ; t)
+
@
@
@x2 @x2
@
@x3
=
en x3 = h + (x1 ; x2 ; t)
con y
como incógnitas. En particular, la forma que adopta la super…cie del
agua se debe obtener como parte de la solución por lo cual (A ) es un problema
de frontera libre.
Supondremos que el estanque o canal es angosto y largo para ignorar la dependencia en x2 y considerar x1 2 [0; 1). Finalmente, usamos las variables x; z en
lugar de x1 ,x3 :
Usando las longitudes características: a, l y h que son la amplitud, longitud
de onda y la profundidad en reposo, de…nimos variables adimensionales
x =
x
l
, z =
z
h
,
=
a
, t =
t
,
=
p
con = plgh ,
= a l hg
La super…cie libre es z = 1 +
con
= ha
Quitando asteriscos a las nuevas variables, (A ) se convierte en
(A )
(i)
(ii)
zz
= 0 en 0 < z < 1 +
z (x; 0; t)
(iii)
+
(iv)
z
=
t
+
2
(
=0
2
x
2
t
+
para t
+
2 2
z
x x)
(x; t) , x > 0
0
= 0 en z = 1 +
en z = 1 +
(x; t)
(x; t)
69
donde = hl . Nos interesa el régimen de poca profundidad (h << 1), amplitud
pequeña (a << 1), onda larga (l >> 1), así que << 1, << 1. Tomamos
2
= O( ), reescalamos ypusamos una coordenada espacial
que se mueve con
p
3=2
velocidad 1, es decir, =
(x t), =
t, =
para obtener
(A)
i)
zz
ii)
z(
iii)
+
iv)
z
+
= 0 en 0 < z < 1 +
; 0; ) = 0
+
= (
para
+
1
2
+
0
2
z
z
( ; )
2
+
+
= 0 en z = 1 +
) en z = 1 +
( ; )
( ; )
Suponemos expansiones de la forma
( ; z; ) = o ( ; z; ) +
( ; ) = o( ; ) +
A orden
0
1(
; z; ) + O(
2
)
1 ( ; ) + O(
2
)
obtenemos
@2 o
@z 2
= 0 en 0 < z < 1 +
@ 1
@z (
por lo cual
o(
; 0; ) = 0
; z; ) no depende de z, es decir
o(
( ; )
@
@
; )=
o
=
o(
; ). Además,
en z = 1
o
Por lo tanto
o(
A orden
1
; )=
@
@
o
( ; )
tenemos
@2 1
@2
@z 2 + @
@ 1
@z ( ; 0;
o
2
=0
)=0
por lo cual
( ; z; ) =
z2 @ 2
2 @
o
2
( ; ) + c( ; )z + b( ; )
Usando la condición de frontera en z = 0 obtenemos
1(
; z; ) =
1(
; )
z2 @ 2
2 @
o
2
( ; )
De la primera condición de frontera en z = 1 obtenemos
1
@
@
1
+
1 @3
2 @
o
3
+
@
@
o
+
1
2
@
@
2
o
=0
(1)
70
APÉNDICE A. KORTEWEG-DE VRIES
y de la segunda se obtiene una relación de consistencia.
A orden
2
obtenemos
@2 2
@2
@z 2 + @
@ 2
@z ( ; 0;
1
2
=0
)=0
Esto implica que
2(
; z; ) =
2(
z2 @ 2
2 @
; )
1
2
z4 @ 4
24 @
( ; )+
o
4
n
o
@
@
@
@
@
Pero := @ j ; @ j ; @zj ; @ j ; @ j tienen segundas derivadas continuas por lo
que toda f 2 tiene la siguiente expansión:
f( ; 1 +
@f
@z (
; ) = f ( ; 1; ) +
2
; 1; ) + O(
)
Por lo tanto
@ 2
@2 2
+
@z
@z 2
o
@2
@
=
1
2
+
1 @4
6 @
@2
@
o
4
o
2
Integramos (9) con respecto a , usando (8) y
@
@
1
2
2
+
o
1 @3
6 @
o
3
@
@
@
@
0
1 @3
6 @
=
1
@
@
=
o
1
o
=
+
@
@
@
@
0
1
o
+
+
@
@
o
+
@
@
o
@
@
o
(2)
para obtener
@
@
1
2
2
o
así que
1
@
@
1
=
@
@
2
+
o
1 @3
2 @
=
o
3
@
@
o
3
0
1
2
@
@
2
o
Es decir,
2 @@ o +
Derivando con respecto a
o
3
+
3
2
@
@
2
=0
o
obtenemos la ecuación
@
@
Reescalando las variables
Korteweg y de Vries
1 @3
3 @
o
+
3
1@
6 @
o
3
+
@
3
2 o @
= 6t, x = , u =
o
=0
3
2 o,
ut + uxxx + 6uux = 0
.
obtenemos la ecuación de
(3)
Bibliografía
[AB] Gert Almkvist, Bruce Berndt.Gauss, Landen, Ramanujan, the ArithmeticGeometric Mean, Ellipses, , and the Ladies Diary.American Mathematical
Monthly 1988. No.August-September. Pp585-608.
[Ca] Max Caspar. Kepler. Dover Publications, 1993.
[Co] John B. Conway. Functions of One Complex Variable. Springer-Verlag,Graduate
Texts in Mathematics, 1978.
[CJ] Richard Courant, Fritz John. Introduction to Calculus and Analysis, Volume 1.Springer, 1998.
[Fl] Gilberto Flores.Ondas viajeras en modelos físicos y biológicos. XVI Escuela
Venezolana de Matemáticas. 2003.
[K] Morris Klein. Calculus: An Intuitive and Physical Approach.Dover Publications, 1998.
[WW] E.T. Whittaker, G.N. Watson. A Course of Modern Analysis. Cambridge
Mathematical Library, 1996.
71