FORMULARIO Potencias. Monofásico (fase – neutro) Potencia

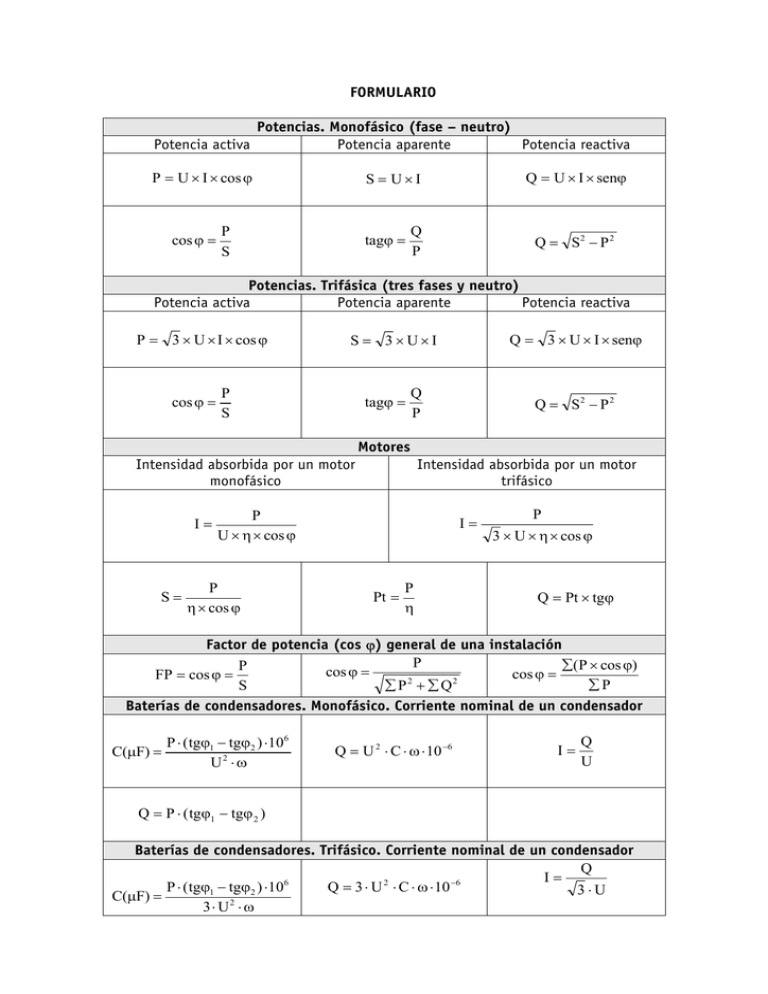
FORMULARIO
Potencias. Monofásico (fase – neutro)
Potencia activa
Potencia aparente
Potencia reactiva
P = U × I × cos ϕ
cos ϕ =
Q = U × I × senϕ
S = U×I
P
S
tagϕ =
Q
P
Q = S2 − P 2
Potencias. Trifásica (tres fases y neutro)
Potencia activa
Potencia aparente
Potencia reactiva
P = 3 × U × I × cos ϕ
cos ϕ =
Q = 3 × U × I × senϕ
S = 3×U×I
P
S
tagϕ =
Q
P
Q = S2 − P 2
Motores
Intensidad absorbida por un motor
monofásico
I=
S=
Intensidad absorbida por un motor
trifásico
P
U × η × cos ϕ
P
η × cos ϕ
I=
Pt =
P
η
P
3 × U × η × cos ϕ
Q = Pt × tgϕ
Factor de potencia (cos ϕ) general de una instalación
P
∑(P × cos ϕ)
P
cos ϕ =
cos ϕ =
FP = cos ϕ =
2
2
∑P
∑P + ∑Q
S
Baterías de condensadores. Monofásico. Corriente nominal de un condensador
P ⋅ ( tgϕ1 − tgϕ2 ) ⋅106
C(µF) =
U2 ⋅ ω
Q = U 2 ⋅ C ⋅ ω ⋅ 10 −6
I=
Q
U
Q = P ⋅ ( tgϕ1 − tgϕ 2 )
Baterías de condensadores. Trifásico. Corriente nominal de un condensador
Q
I=
6
2
−6
P ⋅ ( tgϕ1 − tgϕ2 ) ⋅10
Q = 3 ⋅ U ⋅ C ⋅ ω ⋅ 10
3⋅U
C(µF) =
2
3⋅ U ⋅ ω
Q = P ⋅ ( tgϕ1 − tgϕ 2 )
I
Intensidad. Intensidad absorbida por el motor. (A)
P
Potencia activa. Potencia nominal del motor, potencia en el eje. (W)
S
Potencia aparente (VA)
Q
Potencia reactiva (VAr)
η
Rendimiento
Pt
Potencia activa absorbida de la red por un motor (W)
U
Tensión de línea para suministros trifásicos. Tensión de fase para suministros
monofásicos. (V)
FP = cosϕ
Factor de potencia.
cosϕ1 Factor de potencia antes de la compensación.
cosϕ2 Factor de potencia después de la compensación
tagϕ1 Tangente antes de la compensación.
tagϕ2 Tangente después de la compensación.
C
Capacidad
ω
pulsación. ω = 2 π f
Expresiones para calcular la sección de un conductor
Las expresiones para calcular la sección de un conductor son:
S=
2× L× P
γ×e× U
En función de la intensidad:
S=
2 × L × I × cos ϕ
γ×e
b) Para líneas trifásicas:
S=
L×P
γ×e× U
En función de la intensidad:
S=
a) Para líneas monofásicas:
[1]
[2]
3 × L × I × cos ϕ
γ×e
Donde:
L
Longitud en metros de la línea.
P
Potencia del receptor que va a alimentar la línea,
γ
Conductividad del conductor (m/Ω.mm2) y que es la inversa de la resistividad.
e
caída de tensión (c.d.t.) en voltios.
U
Tensión nominal de la línea, (normalmente 400 V para líneas trifásicas y 230
entre fase y neutro).
Estas expresiones son aproximadas, ya que no tienen en cuenta la caída de
tensión debida a las inductancias de los cables y el efecto pelicular, los cuales son
despreciables en baja tensión para cables menores de 120 mm2, que son los habituales
tanto en instalaciones de enlace como para instalaciones interiores, por tanto las
consideramos válidas.
De otra parte la siguiente ecuación proporciona el valor de la resistividad de un
material en función de la temperatura
ρT = ρ20 (1 + α20 x ∆T) [3]
ρT
Resistividad del conductor a la temperatura T en Ω·mm2/m
ρ20 Resistividad del conductor a 20 ºC
α20:
Coeficiente térmico para 20 ºC (ºC-1). Coeficiente de variación de resistencia
específica por la temperatura del conductor
∆T
Diferencia de temperatura (∆T = T- 20)
Tabla 1. Resistividad del cobre, aluminio y Almelec, a 20, 70 y 90 ºC, y coeficiente α
Material
Cobre
Aluminio
Almelec (Al-Mg-Si)
ρ20 (Ω.mm2/m)
0,018
0,029
0,032
ρ70(Ω.mm2/m)
0,021
0,033
0,038
ρ90(Ω.mm2/m)
0,023
0,036
0,041
α (ºC-1).
0,00392
0,00403
0,00360
Según esto, la conductividad la podemos obtener por cualquiera de las expresiones
siguientes:
γ 20 º C
1
ó
γT =
[4]
γT =
1 + α 20 (T − 20º C )
ρT
γ Cu (20º) = 56 m/Ω·mm2
γ Al (20º) = 35 m/Ω·mm2
Tabla 2. Conductividades del cobre y del aluminio para diversas temperaturas, obtenidas
de la expresión indicada.
Conductividad, γ
m/Ω·mm2
Cobre (Cu
Aluminio Al
20 ºC 30 ºC
56
35
54
34
40 ºC
50 ºC
60 ºC
52
32
50
31
48
30
70 ºC 80 ºC
47
29
45
28
90 ºC
44
27
La expresión propuesta en la Guía Técnica de Aplicación del REBT, para calcular la
temperatura real de un conductor en función de la corriente que transporta y de la
máxima corriente que podría transportar y de su aislamiento es:
T = To + (Tmax
 I
− To)
 I max



2
[5]
T = T0 + ( Tmax – T0 ) ( I / Imax )2
Donde:
T
Temperatura real estimada en el conductor
T0
Temperatura ambiente (40º C al aire y 25º C enterrados)
Tmax
Máxima temperatura admisible según su aislamiento 70º C para PVC y 90º C para
XLPE o EPR
I
Intensidad por el conductor
Imax
Intensidad máxima admisible en el conductor por criterio térmico
Procedimiento de cálculo de secciones para la temperatura real de trabajo del conductor:
1. Se calcula la sección para el caso más desfavorable, esto es para la máxima
temperatura que puede soportar según su aislamiento (70º C para PVC y 90º C
para XLPE o EPR) aplicando la expresión [1] ó [2], según corresponda.
2. Se elige el valor comercial más próximo por exceso y se comprueba en las tablas
del REBT (ITC-BT-06, ITC-BT-07, ó ITC-BT-19) que el valor de sección obtenido
cumple con el criterio de calentamiento, esto es, soporta la corriente a
transportar.
3. Si la sección encontrada no cumple con el criterio de calentamiento, se elige la
que cumpla y el proceso ha concluido. En este caso el criterio más crítico o que
más cuesta cumplir habría sido el de criterio térmico.
4. Si la sección comercial obtenida en el apartado 2 si cumple con el criterio de
calentamiento, realizamos una nueva iteración: elegimos el valor de sección
inmediatamente inferior y volvemos a comprobar si esta nueva sección cumple
con el criterio de densidad de corriente. Si no cumple, nos quedamos con la
sección inicial. Por el contrario, si cumple calculamos la temperatura real del
conductor para esta sección, para ello utilizamos la ecuación [5].
5. A partir del valor de la temperatura real del conductor, calculamos su
conductividad a esa temperatura utilizando la ecuación [4]
6. Con el nuevo valor de la conductividad calculamos el valor de la sección mínima
para cumplir con la caída de tensión y verificamos en las tablas que también
cumple con el criterio térmico.