Se considera una ventana cuya parte inferior es un
Anuncio

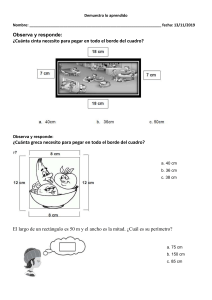
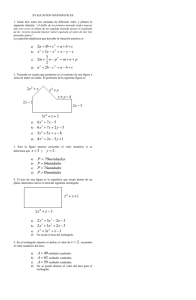
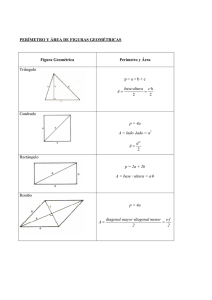
Se considera una ventana cuya parte inferior es un rectángulo y la superior, un semicírculo. Si el perímetro de la ventana es de 6 m, calcula las dimensiones de la parte rectangular para que entre un máximo de luz. En primer lugar, es evidente que el radio del semicírculo es la mitad de la base del rectángulo, con lo que las incógnitas o variables del problema son sólo x e y. La condición que nos ponen es que el perímetro es 6m. Hay que sumar tres lados rectos y media circunferencia: x 6 2 Por otra parte, la función que hay que maximizar es el área: x 2y x f ( x, y ) x y ( ) 2 / 2 2 Despejo y en la condición de arriba para sustituir y obtener una función con una sola variable: y 6 x 2 f ( x) x (3 f ' ( x) 3 x 2 3 x x 2 4 x x x x2 x2 x2 x2 x2 ) ( ) 2 / 2 3x 3x 2 4 2 2 4 8 2 8 2x x x 3 x 2 4 4 f ' ( x) 0 x 0 3 x 4 12 4 x x 0 4 12 x(4 ) 0 12 1.68 x 4 12 es un posible máximo o mínimo, pero hay que tener en 3 cuenta también los extremos del intervalo de x. X puede variar entre 0 y el valor que obtenemos al suponer y=0 en: x x 2y 6 2 6 x 2.3339 1 2 Hallamos los valores de la función en 0, 1.68 y 2.33, obteniendo, más o menos: El valor x f (0) 0 f (1.68) 2.52 f (2.33) 2.15 Por lo tanto x=1.68 es la respuesta al problema. Pintando la función en geogebra lo confirmamos: