PROBLEMAS DE ACÚSTICA HOJA N 1

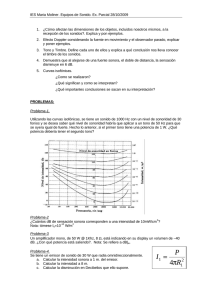
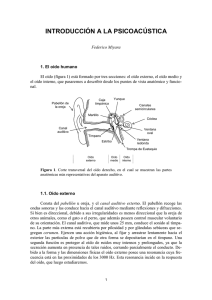
PROBLEMAS DE ACÚSTICA
HOJA N0 1
I. 1. - Un tono puro tiene un nivel de sonoridad de 50 fonios y 1000 Hz de frecuencia. Determine
cuantos tonos análogos a éste deben actuar simultáneamente, para producir un nivel sonoro que sea el doble del
producido por un sólo tono.
I. 2. - Dados tres tonos puros con las siguientes frecuencias y niveles de presión; 100 Hz - 60 dB, 200
Hz - 60 dB, 500 Hz - 55 dB. Averigüe:
a) Cuál es el tono de mayor nivel de sonoridad.
b) el nivel de intensidad total cuando suenan simultáneamente los 3 tonos.
c) la sonoridad total en sonios.
I. 3. - Dados 6 tonos puros con las siguientes frecuencias y niveles de intensidad; 50 Hz -85 dB, 100
Hz - 80 dB, 200 Hz - 75 dB, 500 Hz - 80 dB, 1000 Hz - 75 dB, 10000 Hz - 70 dB. Determine:
a) el nivel de sonoridad, en fonios, para cada uno de los 6 tonos.
b) el nivel de intensidad total (actuación simultánea)
c) la sonoridad total en sonios.
Si el nivel de intensidad para cada uno de los tonos disminuye en 30 dB, determine:
d) los nuevos valores del nivel de sonoridad para cada tono
e) el nivel de intensidad total (actuación simultánea)
f) el nivel de intensidad requerido por un tono puro de 1000 Hz que posea el mismo nivel que en el apartado
anterior
I. 4. - Una explosión tiene un nivel sonoro de 100 dB a 10 metros de distancia del sitio donde se
produce. Si el valor de la intensidad mínima necesaria para detectarse es de 5·10-6 W/m2, calcule la distancia a la
que deja de ser audible, así como su potencia.
Nota: en ondas esféricas la intensidad decrece con el cuadrado de la distancia.
I. 5. - Una máquina produce en un cierto punto un ruido cuyo nivel de sonoridad es 70 fonios; calcule
el nivel, en el mismo punto, cuando están trabajando simultáneamente 5 máquinas idénticas a la primera.
I. 6. – Un amplificador de sonido entrega una salida con un nivel de potencia de 25 dB superior al nivel
de potencia de la entrada; si la potencia de salida es de 3 mW, calcule la potencia de entrada.
I. 7. - Si la presión ejercida por las ondas acústicas sobre la membrana timpánica del oído viene dada
por p = p 0 cos ( ω t ) y la respuesta del sistema auditivo se puede poner como:
r = a p + b p2 + c p3
donde a, b y c son constantes; demuestre que dicha respuesta contiene un término constante y 3 términos de
frecuencias, 2ω y 3ω, y calcule sus amplitudes de presión en función de p0 y de las constantes a, b y c.
I. 8. - Un foco sonoro emite un tono puro de 1000 Hz. Disponemos de dos sonómetros idénticos
situados en dos puntos A y B tales que las distancias al foco son rA y rB = 4 rA respectivamente. Calcule la
diferencia entre los niveles de intensidad sonora que indican los dos sonómetros.
I. 9. - Un ruido tiene un espectro tal que su intensidad, en cada banda de 1 Hz, está dada por
−6
I1 = 10 / f
( W m −2 Hz −1 ) donde "f" es la frecuencia central de la banda en Hz. Calcule:
a) el nivel de intensidad espectral a las frecuencias de 100, 500 y 1000 Hz.
b) el nivel de intensidad de la banda de frecuencias entre 100 y 1000 Hz.
*I. 10. - El ruido en los alrededores del área de trabajo de una cortadora de metal fue analizado en
bandas de octava, dando como resultado los valores de la siguiente tabla:
Frecuencia central en Hz
Nivel de intensidad en banda en dB
31,5
74
63
79
125
80
250
87
500
83
1000
83
2000
93
4000
98
8000
91
16000
86
a) ¿Cuál es la sonoridad en sonios, según el método de Stevens?
b) ¿Cuál es el nivel de presión sonora conjunto, en decibelios, sabiendo que la impedancia característica del
medio es ρc = 400 R?
c) Si se aísla la máquina de modo que se reduce el nivel de banda en la banda de 4000 Hz a un valor de 60 dB,
¿se modifican sustancialmente las respuestas dadas en los apartados anteriores?