Tablas de verdad o Valores de verdad

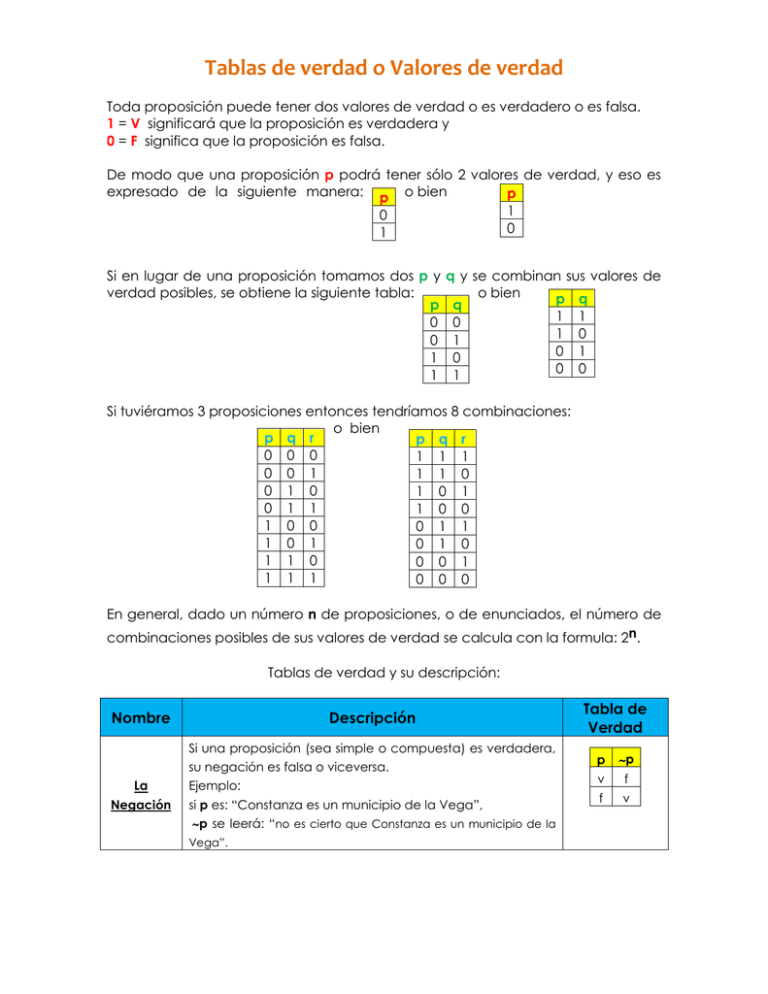
Tablas de verdad o Valores de verdad
Toda proposición puede tener dos valores de verdad o es verdadero o es falsa.
1 = V significará que la proposición es verdadera y
0 = F significa que la proposición es falsa.
De modo que una proposición p podrá tener sólo 2 valores de verdad, y eso es
expresado de la siguiente manera: p o bien
p
1
0
0
1
Si en lugar de una proposición tomamos dos p y
verdad posibles, se obtiene la siguiente tabla:
p
0
0
1
1
q y se combinan sus valores de
o bien
p q
q
1 1
0
1 0
1
0 1
0
0 0
1
Si tuviéramos 3 proposiciones entonces tendríamos 8 combinaciones:
o bien
p q r
p q r
0 0 0
1 1 1
0 0 1
1 1 0
0 1 0
1 0 1
0 1 1
1 0 0
1 0 0
0 1 1
1 0 1
0 1 0
1 1 0
0 0 1
1 1 1
0 0 0
En general, dado un número n de proposiciones, o de enunciados, el número de
combinaciones posibles de sus valores de verdad se calcula con la formula: 2n.
Tablas de verdad y su descripción:
Nombre
Descripción
Si una proposición (sea simple o compuesta) es verdadera,
su negación es falsa o viceversa.
La
Negación
Ejemplo:
si p es: “Constanza es un municipio de la Vega”,
p se leerá: “no es cierto que Constanza es un municipio de la
Vega”.
Tabla de
Verdad
p
p
v
f
f
v
Nombre
Tabla de
Verdad
Descripción
La
conjunción
O producto: nos esta indicando que la proposición será
símbolos:
and, , y, *
verdadera si ambas acciones se cumplen.
Nombre
Descripción
La
O incluyente: significa que la verdad se dará cuando
disyunción
realice al menos una de las acciones.
Inclusiva
Como conclusión se puede decir que la disyunción es
símbolos:
verdadera si al menos uno de los disyuntivos también lo
v, o, +
es.
Nombre
La disyunción
exclusiva
p
q
pq
v
v
v
v
f
f
f
v
F
f
f
F
Tabla de
Verdad
p
q
pq
v
v
v
v
f
v
f
v
v
f
f
F
Tabla de
Verdad
Descripción
Esta solo será verdadera cuando las dos proposiciones
que la componen tienen diferentes valores de verdad,
en caso contrario es falsa.
Nombre
Descripción
La
pq donde p se denomina antecedente y q
Condicional
consecuente.
o
Una condicional solo es falsa cuando su antecedente es
Implicación
símbolo: 
verdadero y el consecuente es falso; en los demás casos
la condicional es verdadera.
p
q
pq
v
v
f
v
f
v
f
v
v
f
f
f
Tabla de
Verdad
p
q
pq
v
v
v
v
f
f
f
v
v
f
f
v
Nombre
La verdad de esta proposición se basa en el compromiso
La
Bicondicional
o Doble
Implicación
símbolo: 
doble que existe.
Está solo es verdadera cuando las dos proposiciones que
la forman tienen el mismo valor de verdad, es decir,
cuando ambas sean verdaderas o ambas falsas. En caso
contrario la Bicondicional es falsa.
Concepto de Tautología
Una
Tabla de
Verdad
Descripción
proposición
compuesta
es
lógicamente
verdadera o tautológica cuando es verdadera
siempre, independientemente de los valores de
verdad de las proposiciones simples que la forman.
Ejemplo:
pq
v
v
v
v
f
f
f
v
f
f
f
v
q
pvq
p(pq)
v
v
v
f
v
v
v
v
f
v
v
v
f
f
f
v
La contradicción: es una proposición compuesta que es falsa
independientemente de los valores de verdad de las proposiciones
que la formen. Ejemplo:
Concepto de contingencia
La contingencia: es la combinación de la tautología y la
Ejemplo:
q
p
Concepto de Contradicción
contradicción.
p
p
p
pq
v
f
f
f
v
f
p
q
pq
v
v
v
v
f
f
f
v
v
f
f
v