Examen2doParcial 88KB Dec 10 2014 05:28:57 PM

1. Creative Coffees vende aproximadamente 100 toneladas de grano
de café cada año a los supermercados. El importador de la
compañía carga $1 por libra más $300 por pedido. Cuando se hace
un pedido, le lleva cuatro semanas al socio sudamericano de
Creative Coffees tostar el grano, pasarlo por las aduanas y hacerlo
llegar a la planta de Creative. $50 adicionales cubren los costos de
oficina y otros asociados con la orden de pedidos. Suponiendo una
tasa de transferencia anual, i=0.25 utilice las fórmulas EOQ para
determinar:
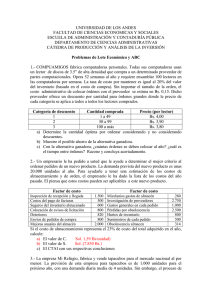
Se tiene un inventario de un producto con la siguiente forma:
Nivel de
Inventario
R
T1
T2
Datos
 = 100 [Ton/año]
h = 1 [$/Lib]*i = 500 [$/Ton]
K = 300 [$]+50 [$] = 350 [$]
T1 = 4 [Semanas] = 0.08 [años]
Como:
R
T1
P  T1    T1
R
P
( 1)
Tiempo
Y:


2 K 1 
R


P
( 2)
h
Donde: P = Volumen de Producción.
El volumen de producción podemos hallar reemplazando (2) en (1).


2 K 1 


P
h
T1
P
Reemplazando valores obtenemos la siguiente ecuación:
3.2P2 –320P –70000 = 0
P1 = 206.12
P2 =-106.12
El valor positivo representa el volumen de producción, de esta manera ya se
cuenta con todos los datos.
a) La cantidad de pedidos óptima, q.
q
2K
16.49Ton


h 1  
P

b) El punto de nuevos pedidos, R.


2 K 1 
R


P
h
8 .48 Ton
c) El número de pedidos por año.
Calculamos el T2:


2 K 1 
T2
h

P



0 .08 5
A ño s
Entonces:
T = T1 + T2 = 0.165 Años.
0.165 Años  1 Pedido
1 Año
 X Pedidos
Entonces si:
X = 6.06 Pedidos por año.
d) El costo anual total.
C


2Kh 1 

 0.0042
P
3. La Ajax Manufacturing Company ha compilado la siguiente
información concerniente a la pieza comprada #5643. El promedio
de consumo es de 120 unidades diarias, con una desviación estándar
de 50 unidades, basada en que la fábrica trabaja 250 días al año. El
costo de adquisición por pedido es de $20. Los costos de
mantenimiento de inventario son de $1 anual, y el tiempo de
adelanto de adquisición es de 10 días, y es constante. LA compañía
ha determinado que solo puede permitirse un agotamiento anual de
las existencias.
Datos
 = 120 [Unid/día] = 30000 [Unid/Año]
D = Desviación estándar de 50 [Unid/día]
h = 1 [$/Año]
K = 20 [$]
T = 10 [días]
La fábrica trabaja 250 días al año.
a) Calcúlese la cantidad económica del pedido.
q
2K
h
1 09 5
U ni dad es
b) Con un sistema de control de inventario de cantidad fija y ciclo
variable, calcúlese la existencia de seguridad requerida y el punto de
renovación de pedido.
Hallamos la tipificación de la curva Normal (Z):

Primero, se halla el porcentaje que se de un agotamiento:
%g
1

 1 00%
3 .6%
q

Se halla el valor de Z en tablas para una probabilidad de 0.464:
Z = 1.79
Entonces:
ExSeg
Z
2
TD
2 83U ni dad es
Finalmente:
RenovPed
T  ExSeg
1483Unidades
c) Con un sistema de control de inventario de cantidad variable y el ciclo fijo,
calcúlese la duración del periodo de revisión y las existencias de seguridad
requerida.
q
PerRev

9días
Entonces la existencia de seguridad se calcula de la siguiente manera:
2
ExSeg Z  ( T  P erRev)D
3 90U ni dad es