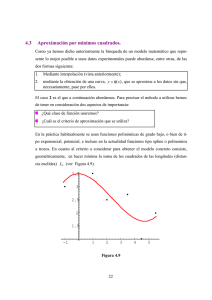
Condición de Frontera Natural - U

• Condición de Frontera Natural: Consideremos los puntos equiespaciados: 0 = 0! 1 = 14 ! 2 = 12 ! 3 =
2
3
4 ! 4 = 1 y la función " ( ) = sin(# )$ Luego: %0 = sin(0) = 0! %1 = sin( 4 ) = 2 ! %2 = sin( 2 ) =
3
2
1! %3 = sin( 4 ) = 2 ! %4 = sin(#) = 0$ Para determinar el sistema (7) se necesita calcular &0 ! &1 ! &2 ! &3
y '0! '1 ! '2 ! '3 ! '4 $ Como los puntos son equiespaciados: &0 = &1 = &2 = &3 = 14 $ Los '" se determinan
de (0): '" = " ( " )
( = 0! 1! $$$! 4$ Luego: '0 = 0! '1 = 22 ! '2 = 1! '3 = 22 ! '4 = 0$ El sistema (7)
queda:
#
#
#
0
)0
1
0
0
0
0
1)
0) $
!
! &0 2(&0 + &1 )
$ ! 3(#2$!#
! 3(#1$!#
&1
0
0 $
$
1
0
!
$ ! )1 $ !
!
$ ! )2 $ = ! 3(#3 !#2 ) ! 3(#2 !#1 ) $
! 0
&
2(&
+
&
)
&
0
$
1
1
2
2
$!
!
$ !
$2
$1
$
" 0
0
&2
2(&2 + &3 ) &3 % " )3 % " 3(#4 !#3 ) ! 3(#3 !#2 ) %
$3
$2
0
0
0
0
1
)4
0
Reemplazando los valores:
1
! 1
! 4
! 0
!
" 0
0
0
1
0
1
4
1
4
1
1
4
0
0
0
0
0
1
4
1
0
0
0
0
1
4
1
#
$!
$!
$!
$!
%"
)0
)1
)2
)3
)4
Cuya solución es:
!
!
!
!
"
)0
)1
)2
)3
)4
#
$ !
$ !
$=!
$ !
% "
#
$ !
$ !
$=!
$ !
% "
0 "
12(1"! 2)
12( 2 !
"2)
12(1 ! 2)
0
0
!3$ 672 3
!5$ 193 3
!3$ 672 3
0
#
$ !
$ !
$=!
$ !
% "
0
!4$ 970 6
!7$ 029 4
!4$ 970 6
0
#
$
$
$
$
%
#
$
$
$
$
%
Finalmente se tienen que determinar los *" y +" $ Para ello se utilizan las ecuaciones:
Luego:
*"
= ('"+1 ! '" )
+"
=
1
&"
! ()"+1 + 2)" )
&"
3
1
()"+1 ! )" )
3&"
( = 0! $$$! , ! 1
( = 0! $$$! , ! 1
#
('1 ! '0 ) $10 ! ()1 + 2)0 ) $30
*0
!
! *1 $ ! ('2 ! '1 ) $1 ! ()2 + 2)1 ) $31
!
$
1
" *2 % = !
" ('3 ! '2 ) $12 ! ()3 + 2)2 ) $32
*3
('4 ! '3 ) $13 ! ()4 + 2)3 ) $33
#
#
1
+0
3$0 ()1 ! )0 )
! +1 $ ! 3$1 ()2 ! )1 ) $ !
!
$ ! 1
$ !
" +2 % = " 1 ()3 ! )2 ) % = "
3$2
1
+3
3$3 ()4 ! )3 )
#
#
3$1344
$ !
$ ! 2$2164 $
$
$="
%
0
%
!2$2164
#
!4$8963
!2$0281 $
$
2$0281 %
4$8963
• Condición de Frontera Sujeta: Consideremos los puntos equiespaciados: 0 = 0! 1 = 14 ! 2 = 12 ! 3 =
3
2
4 ! 4 = 1 y la función " ( ) = cos(# )$ Luego: %0 = cos(0) = 1! %1 = cos( 4 ) = 2 ! %2 = cos( 2 ) = 0! %3 =
cos( 34 ) = ! 22 ! %4 = cos(#) = !1$ Para determinar el sistema (7) se necesita calcular &0 ! &1 ! &2 ! &3 y
'0! '1 ! '2 ! '3 ! '4 $ Como los puntos son equiespaciados: &0 = &1 = &2 = &3 = 14 $ Los '" se determinan
de (0): '" = " ( " )
( = 0! 1! $$$! 4$ Luego: '0 = 1! '1 = 22 ! '2 = 0! '3 = ! 22 ! '4 = !1$ El sistema
4
(7) queda:
2&0
! &0
!
! 0
!
" 0
0
#
&0
0
0
0
2(&0 + &1 )
&1
0
0
&1
2(&1 + &2 )
&2
0
0
&%!2
2(&%!2 + &%!1 ) &%!1
0
0
&%!1
2&%!1
)0
$ ! )1
$!
$ ! )2
$!
% " )%!1
)%
#
!
$ !
$ !
$=!
$ !
% !
"
3(#1 !#0 )
! 3" 0 ( 0 )
$0
3(#2 !#1 )
0)
! 3(#1$!#
$1
0
3(#3 !#2 )
3(#2 !#1 )
!
$2
$1
3(#4 !#3 )
2)
! 3(#3$!#
$3
2
3)
3" 0 ( % ) ! 3(#4$!#
3
#
$
$
$
$
$
$
%
Reemplazando los valores:
1
2
1
4
1
4
!
!
! 0
!
" 0
0
1
1
4
0
0
0
1
4
0
0
1
4
1
0
0
0
1
4
1
1
4
1
2
1
4
0
#
)0
)1
)2
)3
)4
$!
$!
$!
$!
%"
Cuya solución es:
!
!
!
!
"
)0
)1
)2
)3
)4
#
$ !
$ !
$=!
$ !
% !
"
#
$ !
$ !
$=!
$ !
% "
12( 22 !
"1)
12(1 ! 2)
0 "
!12(1 ! 2)
!12( 22 ! 1)
!5$ 193 3
!3$ 672 2
0
3$ 672 2
5$ 193 3
#
!3$ 514 7
$ !
$ ! !4$ 970 6
$ !
0
$=!
$ "
4$ 970 6
%
3$ 514 7
#
$
$
$
$
%
#
$
$
$
$
%
Finalmente se tienen que determinar los *" y +" $ Para ello se utilizan las ecuaciones:
Luego:
*"
= ('"+1 ! '" )
+"
=
1
&"
! ()"+1 + 2)" )
&"
3
1
()"+1 ! )" )
3&"
( = 0! $$$! , ! 1
( = 0! $$$! , ! 1
#
#
('1 ! '0 ) $10 ! ()1 + 2)0 ) $30
*0
0
! *1 $ !
('2 ! '1 ) $11 ! ()2 + 2)1 ) $31 $
!2$2164
$ !
!
$=!
!
$=
" *2 % !
" ('3 ! '2 ) $12 ! ()3 + 2)2 ) $32 % " !3$1344
!2$2164
*3
('4 ! '3 ) $13 ! ()4 + 2)3 ) $33
#
#
#
1
+0
2$0281
3$0 ()1 ! )0 )
! +1 $ ! 3$1 ()2 ! )1 ) $ ! 4$8963 $
!
$ !
$
$ ! 1
" +2 % = " 1 ()3 ! )2 ) % = " 4$8963 %
3$2
1
2$0281
+3
3$ ()4 ! )3 )
#
$
$
%
3
El siguiente teorema presenta un estimación del error de la spline cúbica sujeta:
¯
¯
Teorema: Sea " # - 4 ['! *] con max ¯" (4) ( )¯ = . . Si / es la spline sujeta determinada en los puntos
#"&"'
0
='0
1
0
2
0 ··· 0
%!1
0
%
= *! entonces:
max |" ( ) ! /( )| $
#"&"'
5.
max (
384 0"("(%!1)
(+1
!
()
4
(9)
Un último teorema, que establece la suavidad de la spline es el siguiente:
Teorema: Sea 1 # - 2 ['! *] cualquier función que satisface las condiciones de interpolación sujetas en los
puntos 0 = ' 0 1 0 2 0 · · · 0 %!1 0 % = * para una función " :
1(
0
1(
")
= "(
0)
0
= "(
5
")
0 )! 1
( = 0! 1! $$$! ,
0
(
%)
= " 0(
%)
Entonces, si / es la spline sujeta determinada en esos mismos puntos:
Z#
2
|/( )| + $
'
Z#
|1( )|2 +
(10)
'
Estos 2 resultados justiÞcan el uso de splines. El primer teorema da una cota del error y el segundo
establece una propiedad de optimalidad: la spline sujeta / es la que oscila menos de todas las funciones
"suaves" que interpolan a "$
3
Un ejemplo de la Vida Real:
Construyamos mediante splines cúbicas el contorno de la citroneta de la fotografía:
1) Primero, se realiza la toma de datos usando una malla cuadriculada sobre la fotografía:
6
2) Luego, los datos se tabulan. Los datos sel contorno superior son
(
:"
"
%"
#
0 1
2
3
4
5
6
7
8
9
10 11 12
2 2$7 3$8 6
8
10
13
16 18 21
25 30 36%
5 7$8 9 10 10$2 10$3 10$4 14$5 15 15$4 15$5 14 5
3) Ahora se calculan los elementos de la matriz, considerando las deÞniciones:
&"
2"
3"
(
!&"
!
"2"
3"
(
!&"
!
"2"
3"
(
!&"
!
"2"
3"
0
0$7
2)8
0)7 = 4
3×
1
1$1
1)2
12
1)1 = 11
12
3 × ( 11 ! 4) = ! 96
11
0)1
2
1
( 20
4
2
=
!
1
20
1
10 ) =
3
! 20
8
3
0)4
2
3 = 15
2
1
7
3 × ( 15 ! 4 ) = ! 20
3×
3×
"+1 ! "
%"+1 ! %"
=
&"
= 3 (2" ! 2"!1 )
2
2$2
1
5
2)2 = 11
5
12
3 × ( 11 ! 11 ) = ! 21
11
0)1
3
1
( 30
5
3
=
!
0)1
4
1
( 40
=
!
1
30
1
20 ) =
9
4
=
1
40
2
15 ) =
1
! 20
! 13
40
0
!7
! 10
!0
!
!0
!
!0
!
!0
!
!0
!
!0
!
!0
!
!0
!
!0
!
"0
0
18
5
11
10
11
10
33
5
11
5
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
11
5
42
5
2
0
0
0
0
0
0
0
0
5
11 )
10
5
3
! 1)5
=
! 10
5
3
1
3 × (! 10 ! 40 ) = ! 39
40
00
0
1
3 × ( 10
!
1
10
#
= ! 117
110
$
$
%
#
6
7
$
3
2
$
4)1
41
0)5
1
%
=
=
3
30
2
4
1
1
41
67
3 × ( 41
!
)
=
4
3
×
(
!
)
=
!
30
30
4
30
20
4) Usando las condiciones de borde de spline natural: / (
el sistema queda:
1
0)2
2
3
2
=
0)
00
= 0! / (
%)
#
11
$
6
$
%
! 96 = ! 32
3
3 × (! 32 + 10
) = ! 18
5
= 0! y reemplazando valores,
#
#
#
0
0 0 0 0 0 0 0 0 0
)0
! $ ! 96 $
0 0 0 0 0 0 0 0 0$
$ ! )1 $ ! ! 11
$
! $ ! 21 $
0 0 0 0 0 0 0 0 0$
11 $
$ ! )2 $ ! !117
! $ !
$
2 0 0 0 0 0 0 0 0$
$ ! )3 $ !! 110
$
! )4 $ ! ! 3 $
8 2 0 0 0 0 0 0 0$
$ ! $ ! 20
$
! $ ! 1 $
2 10 3 0 0 0 0 0 0$
$ ! )5 $ ! ! 20 $
! $ !
$
0 3 12 3 0 0 0 0 0$
$ ! )6 $ = ! 467 $
! )7 $ ! ! $
0 0 3 10 2 0 0 0 0$
$ ! $ ! 20
$
! $ ! 7 $
0 0 0 2 10 3 0 0 0$
$ ! )8 $ ! ! 20
$
! $ ! 13 $
0 0 0 0 3 14 4 0 0$
$ ! )9 $ ! ! 40
$
! $ ! 39 $
0 0 0 0 0 4 18 5 0$
$ !)10 $ ! ! 40
$
%
0 0 0 0 0 0 5 22 6% ")11 % " ! 18
5
0 0 0 0 0 0 0 0 1 )12
0
7
5) Se resuelve el sistema aproximando con 4 cifras signiÞcativas con redondeo:
#
#
0
)0
$
!
! )1 $ ! !2$ 482 $
! $ ! 0$188 8 $
$
! )2 $ !
! $ ! !0$193 2 $
$
! )3 $ !
! $ ! 0$071 97 $
$
! )4 $ !
! $ ! !0$169 7 $
$
! )5 $ !
! $ % ! 0$500 9 $
$
! )6 $ !
! $ ! !0$500 7 $
$
! )7 $ !
! $ ! 0$077 07 $
$
! )8 $ !
! $ ! !0$039 77 $
$
! )9 $ !
! $ !0$000 133 4$
$
")10 % !
" !0$163 7 %
)11
0
6) Se construye la spline natural, ( = 0! 1! $$$! 11
/" ( ) = '" + *" ( !
'"
*"
+"
(
!
"
!
! %"
!
! &"
! * +1 !*
"
$
)"
(
!
"
!
! %"
!
! &"
! * +1 !*
"
$
)"
")
+ )" ( !
")
= %"
%"+1 ! %"
&" (2)" + )"+1 )
=
!
&"
3
)"+1 ! )"
=
3&"
2
+ +" ( !
")
3
#
0
1
2
3
4
5
6
2
2$7
3$8
6
8
10
13 $
$
5
7$8
9
10
10$2
10$3
10$4 $
$
0$7
1$1
2$2
2
2
3
3 $
$
4
1$ 091 0$454 5
0$1
0$05
0$03 333 1$ 367 %
0 !2$ 482 0$188 8 !0$193 2 0$071 97 !0$169 7 0$500 9
#
7
8
9
10
11
12
16
18
21
25
30
36$
$
14$5
15
15$4
15$5
14
5$
$
$
2
3
4
5
6
$
%
0$25
0$133 3
0$025
!0$3
!1$ 5
!0$500 7 0$077 07 !0$039 77 0$000 133 4 !0$163 7 0
i) ( = 0
³
/0 ( ) = 5 + 4 !
0)7×(2×0!2) 482)
3
=& /0 ( ) = 7$ 091
ii) ( = 1
2
´
× ( ! 2) + 0 × ( ! 2)2 +
! 9$ 604 ! 1$ 182
³
/1 ( ) = 7$8 + 1$ 091 !
3
2
+ 0$809 3
3
iii) ( = 2
³
/2 ( ) = 9 + 0$454 5 !
( ! 3$8)3
=& /2 ( ) = 0$848 6
2
´
8+2) 482
× ( ! 2$7) ! 2$ 482 × ( ! 2$7)2 + 0)1883×1)1
×
! 33$ 9
´
2)2×(2×0)188 8!0)193 2)
3
! 3$ 623 ! 0$05788
× ( ! 2)3
+ 5$ 297
1)1×(2×(!2) 482)+0)188 8)
3
( ! 2$7)3
=& /1 ( ) = 33$ 94 ! 9$ 038
!2) 482!0
3×0)7
3
8
2!0)188 8
× ( ! 3$8) + 0$188 8 × ( ! 3$8)2 + !0)1933×2)2
×
+ 13$ 69
iv) ( = 3
³
/3 ( ) = 10+ 0$1 !
´
2×(2×(!0)193 2)+0)071 97)
3
2
3
=& /3 ( ) = 7$ 401 ! 0$988 7
+ 0$044 2
v) ( = 4
³
/4 ( ) = 10$2+ 0$05 !
=& /4 ( ) = 1$ 039
2
2×(2×0)071 97!0)169 7)
3
3
! 8$ 818 ! 0$04028
vi) ( = 5
³
/5 ( ) = 10$3+ 0$033 33 !
´
7!0)071 97
×( !8)+0$071 97×( !8)2 + !0)1693×2
×( !8)3
+ 34$ 89
2
3
+ 0$07451
2
viii) ( = 7
3×(2×0)500 9!0)500 7)
3
! 68$ 58 ! 0$111 3
³
/7 ( ) = 14$5 + 0$25 !
3
( ! 16)3
=& /7 ( ) = 90$ 84 ! 5$ 123
2
+ 0$096 3
3
ix) ( = 8
( ! 18)3
=& /8 ( ) = 0$778 1
x) ( = 9
2
´
+ 328$3
´
³
/9 ( ) = 15$4+ 0$025 !
3
´
+ 115$ 3
2
3
+ 0$003325
³
/10 ( ) = 15$5+ !0$3 !
xii) ( = 11
³
/11 ( ) = 14 + !1$ 5 !
5×(2×(0)000 133 4)!0)163 7)
3
3
! 20$ 51 ! 0$01092
6×(2×(!0)163 7)+0)
3
2
=& /11 ( ) = 33$ 53 ! 0$982 2
´
´
4+0)039 77
×( !21)!0$039 77×( !21)2 + 0)000 1333×4
×
! 35$ 68
xi) ( = 10
2
07
×( !18)+0$077 07×( !18)2 + !0)039 77!0)077
×
3×3
4×(2×(!0)039 77)+0)000 133 4)
3
( ! 21)3
=& /9 ( ) = 6$ 201 ! 0$249 3
( ! 25)3
=& /10 ( ) = 0$819 3
7
× ( ! 16) ! 0$500 7 × ( ! 16)2 + 0)077 07+0)500
×
3×2
! 522
3×(2×0)077 07!0)039 77)
3
! 15$ 37 ! 0$01298
9+0)169 7
×( !10)!0$169 7×( !10)2 + 0)500 3×3
×
7!0)500 9
× ( ! 13) + 0$500 9 × ( ! 13)2 + !0)5003×3
×
2×(2×(!0)500 7)+0)077 07)
3
³
/8 ( ) = 15+ 0$1333 !
´
! 79$ 9
vii) ( = 6
( ! 13)3
=& /6 ( ) = 4$ 841
! 8$ 359
3×(2×(!0)169 7)+0)500 9)
3
( ! 10)3
=& /5 ( ) = 25$ 62 ! 2$ 405
³
/6 ( ) = 10$4 + 1$ 367 !
2
×( !6)3
×( !6)!0$193 2×( !6)2 + 0)071 97+0)193
3×2
´
133 4
×( !25)+0$000 133 4×( !25)2 + !0)163 7!0)000
×
3×5
+ 186$ 9
7
× ( ! 30) ! 0$163 7 × ( ! 30)2 + 0+0)163
× ( ! 30)3
3×6
+ 0$009094
9
3
! 353$ 5
7) Finalmente, la spline cúbica es:
/( ) =
&
'
'
'
'
'
'
'
'
'
'
'
'
'
'
'
'
'
'
(
'
'
'
'
'
'
'
'
'
'
'
'
'
'
'
'
'
'
)
/0 ( )
/1 ( )
/2 ( )
/3 ( )
/4 ( )
/5 ( )
/6 ( )
/7 ( )
/8 ( )
/9 ( )
/10 ( )
/11 ( )
si
si
si
si
si
si
si
si
si
si
si
si
# [2! 2$7]
# [2$7! 3$8]
# [3$8! 6]
# [6! 8]
# [8! 10]
# [10! 13]
# [13! 16]
# [16! 18]
# [18! 21]
# [21! 25]
# [25! 30]
# [30! 36]
8) Ahora, tabulando los datos de la parte inferior del escarabajo.Dada su forma, se interpolará por trazos
usando polinomios de 1# y 2# grado:
*
¸
2 3 7
12 36
"
%" 5 4 7$9 3$8 5
(&!2)
i) "0 ( ) = 5 (&!3)
2!3 + 4 3!2 = 7 !
=& "0 ( ) = 7 !
(&!3)(&!12)
(&!3)(&!7)
ii) "1 ( ) = 4 (&!7)(&!12)
(3!7)(3!12) + 7$9 (7!3)(7!12) + 3$8 (12!3)(12!7) = 2$ 969 ! 0$199 4
2$ 969 ! 0$199 4 2 ! 3$ 113
(&!36)
(&!12)
iii) "2 ( ) = 3$8 (12!36)
+ 5 (36!12)
= 0$05 + 3$ 2 =& "2 ( ) = 0$05 + 3$ 2
iv) Luego, esta función por trozos queda:
&
( "0 ( ) si [2! 3]
"1 ( ) si [3! 12]
"( ) =
)
"2 ( ) si [12! 36]
Finalmente, el gráÞco de /( ) y " ( ) es:
10
2
! 3$ 113 =& "1 ( ) =