Problema realizado por Marta Bravo. Enunciado Determinar el valor

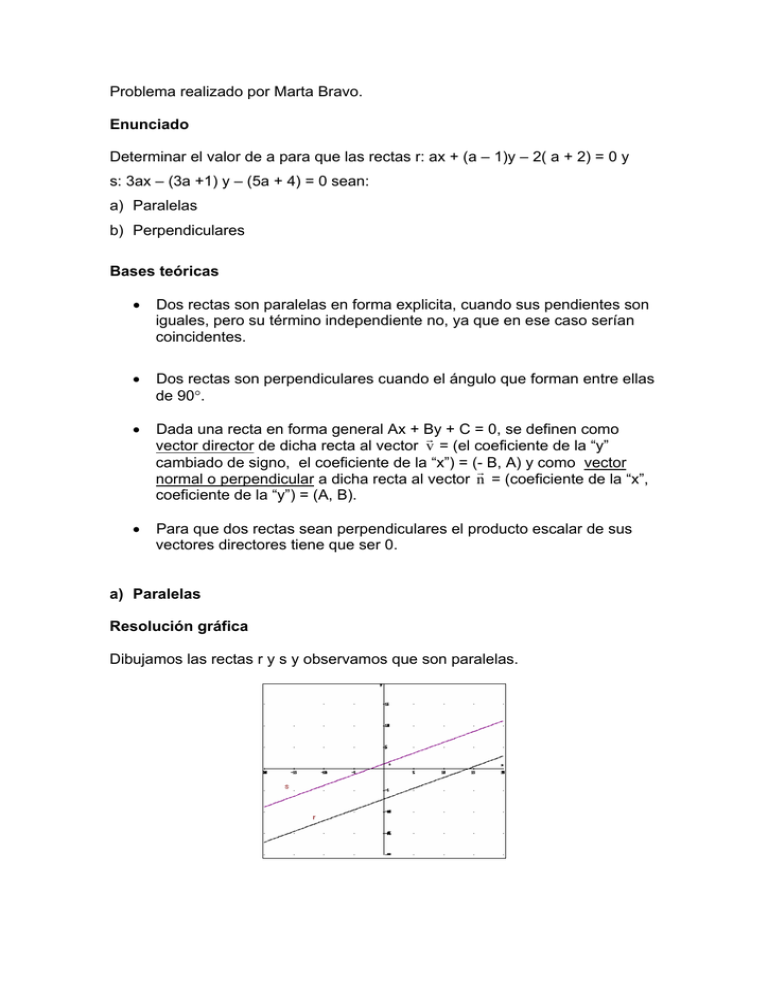
Problema realizado por Marta Bravo.
Enunciado
Determinar el valor de a para que las rectas r: ax + (a – 1)y – 2( a + 2) = 0 y
s: 3ax – (3a +1) y – (5a + 4) = 0 sean:
a) Paralelas
b) Perpendiculares
Bases teóricas
•
Dos rectas son paralelas en forma explicita, cuando sus pendientes son
iguales, pero su término independiente no, ya que en ese caso serían
coincidentes.
•
Dos rectas son perpendiculares cuando el ángulo que forman entre ellas
de 90°.
•
Dada una recta en forma general Ax + By
r + C = 0, se definen como
vector director de dicha recta al vector v = (el coeficiente de la “y”
cambiado de signo, el coeficiente de la “x”) = (-r B, A) y como vector
normal o perpendicular a dicha recta al vector n = (coeficiente de la “x”,
coeficiente de la “y”) = (A, B).
•
Para que dos rectas sean perpendiculares el producto escalar de sus
vectores directores tiene que ser 0.
a) Paralelas
Resolución gráfica
Dibujamos las rectas r y s y observamos que son paralelas.
Cálculos
1. Lo primero es hallar el vector director, la primera componente es el
coeficiente de la y cambiado de signo y la segunda el coeficiente de la x,
para después hallar las pendientes que es la segunda componente partida
de la primera:
a
v
v r = (-a + 1, a) ⇒ mr =
− a +1
r
v s = (3a + 1, 3a) ⇒
ms =
3a
3a + 1
2. Una vez obtenidas las pendientes, las igualamos para saber para que valor
de a son iguales las pendientes.
a
3a
=
⇒ a·(3a+ 1) = 3a (-a+1) ⇒ Simplificamos, dividiendo el
− a + 1 3a + 1
primer miembro y el segundo por “a”, luego una solución es a = 0.Nos
queda por resolver la ecuación siguiente:
3a + 1= 3(-a + 1) ⇒ 3a + 1 = -3a + 3 ⇒ 6a = 2 ⇒ a =
1
3
b) Perpendiculares
Resolución gráfica
Dibujamos las rectas r y s y observamos que son perpendiculares.
Cálculo
Hacemos el producto escalar de los vectores directores de ambas rectas, para
averiguar para que valor de “a” el producto escalar es 0.
v
v r = (-a + 1, a), vector director de la recta r: ax + (a – 1)y – 2( a + 2) = 0
r
v s = (3a + 1, 3a), ), vector director de la recta s: 3ax – (3a +1) y – (5a + 4) = 0
Cálculo del producto escalar:
(-a + 1, a)· (3a + 1, 3a)= 0 ⇒ -3a2 – a + 3a +1 + 3a2 = 0 ⇒ 2a + 1 = 0
⇒
a= −
1
2