Enunciado: Bases Teóricas: Resolución:

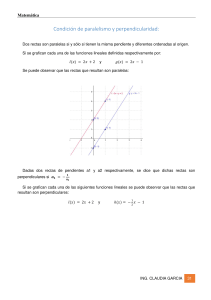
Ejercicio realizado Daniel Pazos Don Pedro.
Enunciado:
Determinar el valor de a para que las rectas: r: ax + (a-1)y – 2(a + 2) = 0 y
s: 3ax – (3a + 1)y – (5a + 4) = 0, sean:
1. Paralelas
2. Perpendiculares
Bases Teóricas:
•
Características de la ecuación general: Ax + By + C = 0
r
u = (coeficiente de la y cambiado de signo, coeficiente de la x) Î
r
u = (-B . A)
•
La pendiente de cualquier recta es: m = tg α =
•
Relación entre pendientes de dos rectas perpendiculares: m1 =
·
r
b
; u = (a , b)
a
−1
m2
Resolución:
Las rectas dadas (r, s), están en forma general, por lo que podemos calcular el
vector director de cada una. Y a partir del vector director la pendiente:
a
r: ax + (a -1)y – 2(a + 2) = 0 Æ u = (-(a – 1), a) Î mr =
− a +1
3a
s: 3ax – (3a + 1)y – (5a + 4) = 0 Æ v = ((3a + 1), 3a) Î ms =
3a + 1
a) r//s (Paralelas Î las rectas no se cortan en ningún punto, las pendientes de
ambas rectas son iguales (mr = ms))
mr = ms
a
3a
=
− a + 1 3a + 1
3a2 + a = -3a2 + 3a
6a2 = 2a
6a2 – 2a = 0
2a (3a - 1) = 0 Î 1ª Solución: 2a = 0; a = 0
2ª Solución: 3a - 1 = 0
a=1/3
b) r ⊥ s (Perpendiculares).
La relación entre las pendientes de dos rectas perpendiculares es:
ms = −
1
mr
⇒
−1
= m1
m2
Sustituyendo:
a -1
3a
=
⇒ 3a2 + 3a + a –1 = 3a2
a
3a + 1
Solución:
⇒ 3a = a –1 ⇒ 2a = -1
-1
2