Problema realizado por Marta Bravo Enunciado Averiguar el valor

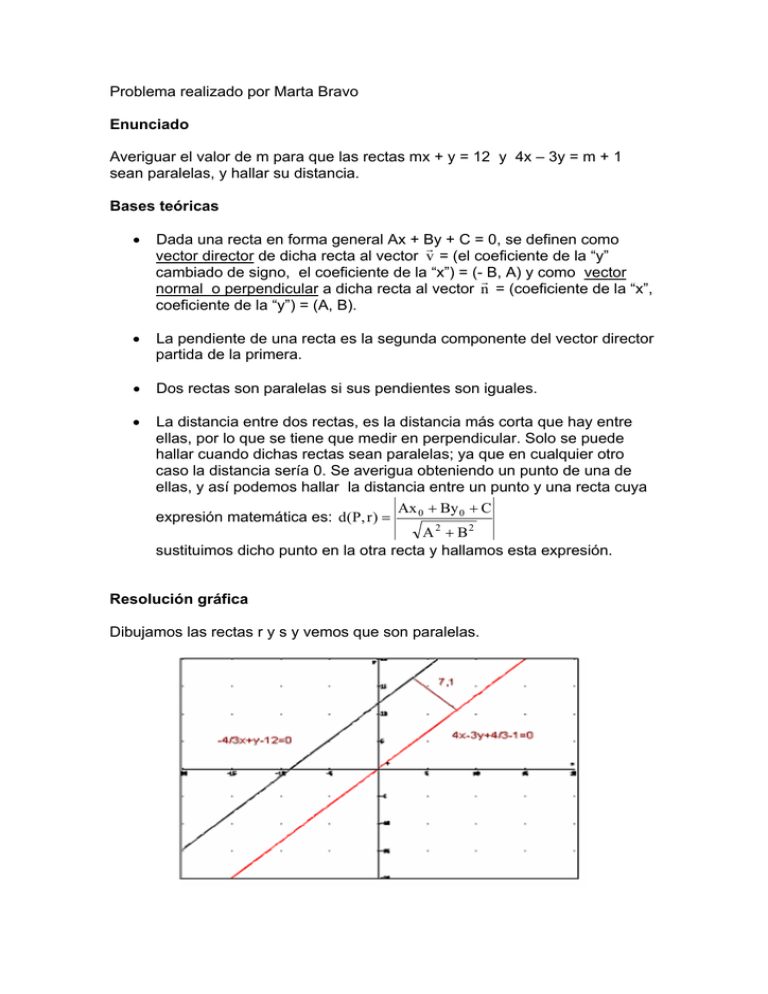
Problema realizado por Marta Bravo
Enunciado
Averiguar el valor de m para que las rectas mx + y = 12 y 4x – 3y = m + 1
sean paralelas, y hallar su distancia.
Bases teóricas
•
Dada una recta en forma general Ax + By
r + C = 0, se definen como
vector director de dicha recta al vector v = (el coeficiente de la “y”
cambiado de signo, el coeficiente de la “x”) = (-rB, A) y como vector
normal o perpendicular a dicha recta al vector n = (coeficiente de la “x”,
coeficiente de la “y”) = (A, B).
•
La pendiente de una recta es la segunda componente del vector director
partida de la primera.
•
Dos rectas son paralelas si sus pendientes son iguales.
•
La distancia entre dos rectas, es la distancia más corta que hay entre
ellas, por lo que se tiene que medir en perpendicular. Solo se puede
hallar cuando dichas rectas sean paralelas; ya que en cualquier otro
caso la distancia sería 0. Se averigua obteniendo un punto de una de
ellas, y así podemos hallar la distancia entre un punto y una recta cuya
Ax 0 + By 0 + C
expresión matemática es: d(P, r ) =
A 2 + B2
sustituimos dicho punto en la otra recta y hallamos esta expresión.
Resolución gráfica
Dibujamos las rectas r y s y vemos que son paralelas.
Cálculos
1. Para hacer que estas dos rectas: mx + y = 12 y 4x – 3y = m + 1 sean
paralelas, lo primero es hallar sus vectores directores:
r
Vector de mx + y = 12 es: v = (- 1, m)
r
Vector de 4x – 3y = m + 1 es: u = (3, 4)
b
v
así podemos
2. Lo último es hallar las pendientes, si x = (a, b) ⇒ m=
a
igualarlas y ver para que valor de m son iguales las pendientes, es decir:
m1=
m2 =
m
= -m, pendiente de la recta mx + y = 12
−1
4
,
3
pendiente de la recta 4x – 3y = m + 1
Igualando pendientes:
-m =
4
3
⇒
m= −
4
3
3. Para hacer el segundo apartado, sustituimos m por el valor hallado en las
dos rectas, y obtenemos un punto cualquiera de una de las rectas, por
4
ejemplo tomamos la recta: − x + y -12= 0, si la x = 0 ⇒ la y vale 12; por
3
lo que tenemos ya un punto P(0, 12). Este punto lo sustituimos la expresión
distancia de un punto a una recta:
d(P,r)=
4·0 − 3·12 + 1 / 3
4 2 + 32
=
− 36 + 1 / 3
16 + 9
−
=
107
3 = − 107 = 7,13
5
15