Problema 21

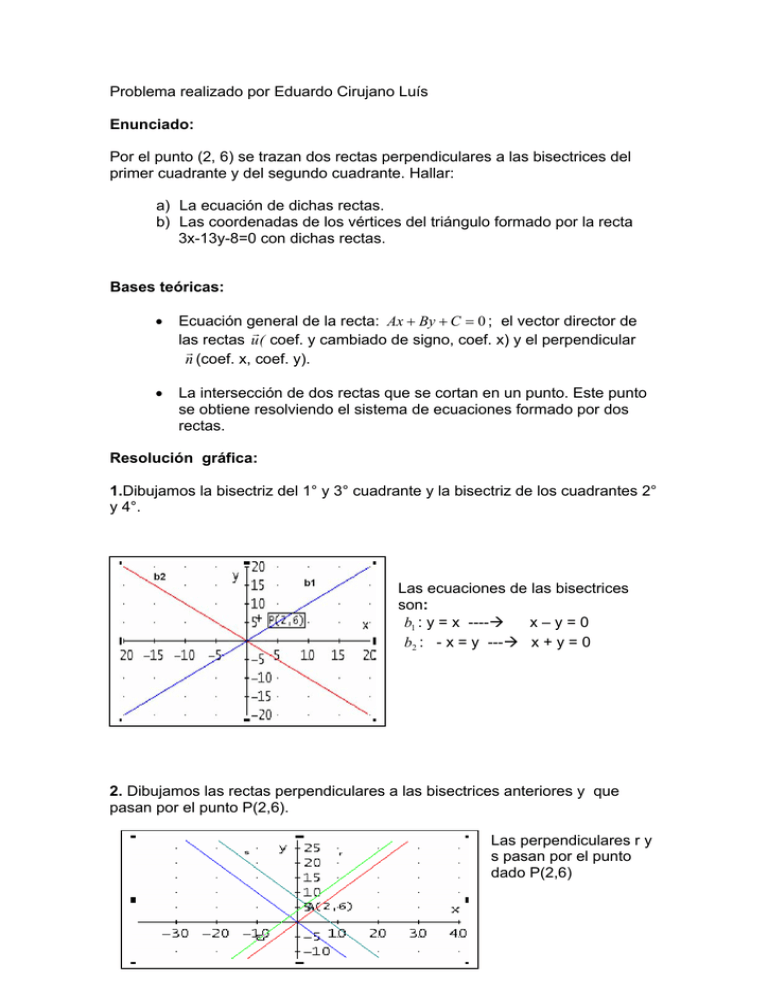
Problema realizado por Eduardo Cirujano Luís
Enunciado:
Por el punto (2, 6) se trazan dos rectas perpendiculares a las bisectrices del
primer cuadrante y del segundo cuadrante. Hallar:
a) La ecuación de dichas rectas.
b) Las coordenadas de los vértices del triángulo formado por la recta
3x-13y-8=0 con dichas rectas.
Bases teóricas:
•
Ecuación general de la recta: Ax + By + C = 0 ; el vector director de
r
las rectas u ( coef. y cambiado de signo, coef. x) y el perpendicular
r
n (coef. x, coef. y).
•
La intersección de dos rectas que se cortan en un punto. Este punto
se obtiene resolviendo el sistema de ecuaciones formado por dos
rectas.
Resolución gráfica:
1.Dibujamos la bisectriz del 1° y 3° cuadrante y la bisectriz de los cuadrantes 2°
y 4°.
Las ecuaciones de las bisectrices
son:
b1 : y = x ----Æ
x–y=0
b2 : - x = y ---Æ x + y = 0
2. Dibujamos las rectas perpendiculares a las bisectrices anteriores y que
pasan por el punto P(2,6).
Las perpendiculares r y
s pasan por el punto
dado P(2,6)
3. Dibujamos el triángulo formado por las perpendiculares de las bisectrices y la
recta dada en el enunciado.
Cálculo:
a) Cálculo de las perpendiculares.
Se calcula la recta r sabiendo que es perpendicular a la bisectriz del primer
cuadrante y pasa por P (2,6)
r
Ecuación de la bisectriz: x − y = 0 el vector director es u ( 1,1 ) que es el vector
normal de la recta r, luego: x + y + k = 0
Para hallar K se sustituyen x e y por las coordenadas del punto que nos dan.
2+6+ k = 0
-8= k
Recta pedida: r: x + y – 8 = 0
Se calcula la recta s sabiendo que es perpendicular a la bisectriz del segundo
cuadrante y pasa por el punto P(2,6)
r
Ecuación de la bisectriz: x + y = 0 el vector director es u ( −1,1 ) que es el
vector normal de la recta r, luego: - x + y + k = 0
Para hallar K se sustituyen x e y por las coordenadas del punto que nos dan
-2+6+ k = 0 ⇒ - 4 = k
Recta pedida: r: - x + y – 4 = 0
b) Cálculo de los vértices del triángulo.
•
Cálculo del punto A = r ∧ s
-----Æ
s: x – y + 4 = 0
Calcular el punto intersección de las rectas obtenidas en el apartado anterior,
rectas r y s:
r: x + y – 8 = 0
s: x – y + 4 = 0
y–4+y–8=0
----Æ2y – 12 = 0 ---Æ y =6
x=y–4
x=6–4=2
Solución del punto A = (2,6)
•
Cálculo del punto B = r ∧ t
Calcular el punto intersección de una de las rectas obtenidas en el
apartado anterior r y la recta dada en el enunciado t:
r: x + y – 8 = 0
x=8–y
t: 3x - 13y – 8 = 0
3(8 – y) – 13y – 8 = 0 -----Æ 24 – 3y – 13y – 8 = 0--Æ-16y + 16 = 0 -----Æ y =1
x=8–1=7
Solución del punto B = (7, 1)
•
Cálculo del punto C = t ∧ s
Calcular el punto intersección de la otra recta s y la recta dada en el
enunciado t:
s: x – y + 4 = 0 ;
t: 3x - 13y – 8 = 0
x=y–4
3(y – 4) – 13y – 8 = 0
3y – 12 -13y – 8 = 0
-10y – 20 = 0
x = -2 – 4 = -6
Solución del punto C = (- 6, - 2)
y=-2