Yovany Gómez - prof.usb.ve.

Tarea 2
Máquinas Eléctricas III
CT-4311
Autor: Yovany Gomez
Carnet: 04-37039
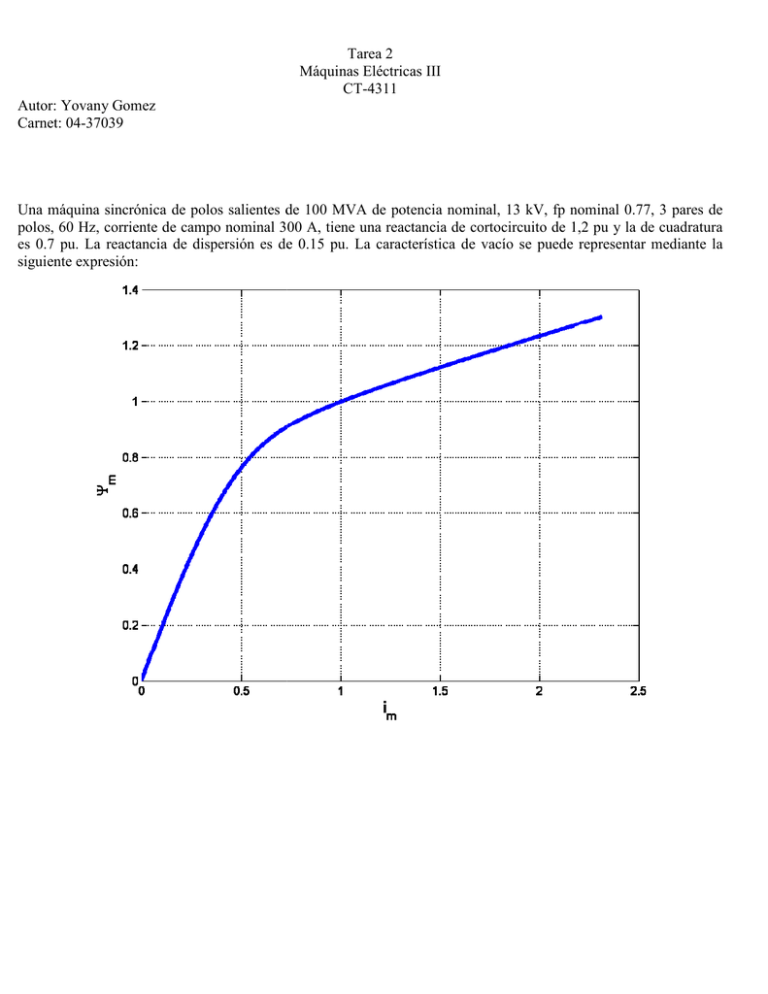
Una máquina sincrónica de polos salientes de 100 MVA de potencia nominal, 13 kV, fp nominal 0.77, 3 pares de
polos, 60 Hz, corriente de campo nominal 300 A, tiene una reactancia de cortocircuito de 1,2 pu y la de cuadratura
es 0.7 pu. La reactancia de dispersión es de 0.15 pu. La característica de vacío se puede representar mediante la
siguiente expresión:
1. Calcule La corriente de campo necesaria para motorizar una carga de 80 MW y -15 MVAR.
%Datos segun el enunciado
Vn=1;
Xd=1.2;
Xq=0.7;
Xsig=0.15;
ifn=300;
S=100;
%Potencia aparente para motorizar la carga
P=-80/S;
Q=15/S;
S1=(P)+(1i*Q);
%Construccion de caracteristica de vacio saturada y lineal
k=1;
Lm0=2;
Lmsat=.2;
PsiT=0.93;
fT=1;
iT = 1/Lm0*PsiT;
Psimax = 4*iT*Lmsat+PsiT;
tauT = fT / PsiT * Lm0/Lmsat;
Mf = 1/Lmsat;
Mi = (1/Lm0 - 1/Lmsat*(.5-atan(tauT*PsiT)/pi))/(.5+atan(tauT*PsiT)/pi);
for Psim=[0:0.0001:1]*Psimax
i_ml=(2)^-1*Psim;
im = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT))PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2)log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
lineal(k,:)=[Psim i_ml];
sat(k,:)=[Psim im];
vec(k,:)=[Psim i_ml im];
k=k+1;
end
%Comienzo del algoritmo directo para calculo de saturacion
I1=conj(S1/Vn);
D=Vn+(1i*Xq*I1);
Ee=Vn+(1i*Xsig*I1);
Eq=abs(Ee)*cos(angle(D)-angle(Ee));
%Obtenido Eq se busca Ifl y Ifs en las respectivas curvas
for n=1:1:length(vec)
if (abs(Eq-vec(n,1)))<=0.0001
ifl=vec(n,2);
ifs=vec(n,3);
satu=ifs/ifl;
end
end
%Valor de la sutaracion
s1=satu;
%coreccion de la reactancia de dispersion
Xds=(Xd/s1)+(((s1-1)/s1)*Xsig);
%calculo de la tension de campo considerando la saturacion
Efs=abs(D)+((Xds-Xq)*abs(I1)*sin(angle(D)-angle(I1)));
%Correccion de la curva lineal para hallar la corriente de campo
for Y=[0:0.0001:1]*1.4*Psimax
i_ls=s1*(2)^-1*Y;
ils(k,:)=[Y i_ls];
k=k+1;
end
for n=1:1:length(ils)
if (abs(Efs-ils(n,1)))<=0.0001
ifcampo1=ils(n,2);
end
end
%Calculo de la corriente de campo en valores reales
if1=ifcampo1*ifn ;
%Graficacion de curva saturada, curva lineal y curva corregida
plot(sat(:,2),sat(:,1))
ylabel('\Psi_m');
xlabel('i_m');
grid on;
hold on
plot(lineal(:,2),lineal(:,1))
grid on;
hold on
plot(ils(:,2),ils(:,1))
%Resultados
Ifcampo = 1.1501 (pu)
Ifcampo = 345.0381 (Amperes)
Efs = 1.2487 (pu)
ifl =0.4832
(pu)
ifs =0.8900
(pu)
s1 =1.8420
(pu)
Eq=0.9663
(pu)
Xds=0.72
(pu)
Solucion grafica del punto de operacion del campo para la entrega de potencia solicitada
2. Determine el ángulo de carga y los reactivos requeridos cuando se acciona el generador con 60 MW y
corriente de campo máxima.
%Construccion de caracteristica de vacio saturada y lineal
k=1;
Lm0=2;
Lmsat=.2;
PsiT=0.93;
fT=1;
iT = 1/Lm0*PsiT;
Psimax = 4*iT*Lmsat+PsiT;
tauT = fT / PsiT * Lm0/Lmsat;
Mf = 1/Lmsat;
Mi = (1/Lm0 - 1/Lmsat*(.5-atan(tauT*PsiT)/pi))/(.5+atan(tauT*PsiT)/pi);
for Psim=[0:0.0001:1]*Psimax
i_ml=(2)^-1*Psim;
im = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
lineal(k,:)=[Psim i_ml];
sat(k,:)=[Psim im];
vec(k,:)=[Psim i_ml im];
k=k+1;
end
%Declaracion de variables globales
global Vn Xd Xq Xsig ifn S ifmax P2 V Xds Efs
%Datos segun el enunciado
Vn=1;
Xd=1.2;
Xq=0.7;
Xsig=0.15;
ifn=300;
S=100;
%Comienzo del algoritmo indirecto para calculo de punto de operacion
%Valores de Partida
ifmax=1.1501;
P2=60/S;
V=Vn;
%Primera supocision de valor de saturacion
s(1)=1;
%ciclo iterativo en el cual se suponen valores de saturacion hasta que
%el valor supuesto es igual a el valor calculado
for k=1:1:40
% k=numero de iteraciones
%Calculo de parametros
Xds=(Xd/s(k))+(((s(k)-1)/s(k))*Xsig);
Efs=(2/s(k))*ifmax;
%Busqueda del angulo de carga mediante funcion externa
%Esta funcion va fuera del algoritmo se presenta en el texto
%por simplicidad
function F = myfun(y)
global Xq P2 V Xds Efs
F=(((Efs*V)/Xds)*sin(y(1)))+((V^2/2)*((((1/Xq)-(1/Xds))*sin(2*y(1)))))-P2;
end
%valor inicial del angulo de carga y solucion de la ecuacion trascendental
x0=[0.6];
[y,fval] = fsolve(@myfun,x0);
%Calculo de la potencia reactiva
Qk=(((Efs*V)/Xds)*cos(y))-((V^2)*((((cos(y)^2)/Xds)+((sin(y)^2)/Xq))));
%Calculo de la corriente de armadura cuando se tienen P y Q
S2=(P2)+(1i*Qk);
I2=conj(S2/V);
%Calculo de vectores del diagrama fasorial
Ee=V+(1i*Xsig*I2);
D=V+(1i*Xq*I2);
%obtencion de la tension del campo en cuadratura
Eq=abs(Ee)*cos(angle(D)-angle(Ee));
%Obtenido Eq se busca Ifl y Ifs en las respectivas curvas
for n=1:1:length(vec)
if (abs(Eq-vec(n,1)))<=0.001
ifl=vec(n,2);
ifs=vec(n,3);
satu=ifs/ifl;
end
end
%valor de saturacion supuesto de entrada
satuin=s(k);
%valor de saturacion calculado de salida
s(k+1)=satu;
%vector solucion
sol(k,:)=[k satuin Xds Efs (y*180/pi) Qk abs(I2) angle(I2)*180/pi Eq satu];
%Si valor de saturacion calculado es igual al supuesto entonces se guarda
%ese valor
if abs(s(k+1)-s(k))<=0.001
saturacion=s(k+1);
end
%si no coinciden se comienza el ciclo con el ultimo valor calculado
end
Tabla resumen de iteraciones para la condición solicitada
Iteracion
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
Sat in
1,000
2,758
1,455
2,369
1,652
2,202
1,763
2,108
1,832
2,051
1,876
2,015
1,904
1,993
1,921
1,979
1,932
1,969
1,940
1,964
1,944
1,960
1,948
1,957
1,950
1,956
1,950
1,955
1,951
1,954
1,952
1,954
1,952
1,953
1,953
1,953
Xds
1,2000
0,5307
0,8718
0,5933
0,7857
0,6269
0,7454
0,6480
0,7231
0,6619
0,7097
0,6710
0,7016
0,6769
0,6965
0,6807
0,6933
0,6832
0,6913
0,6847
0,6900
0,6858
0,6891
0,6865
0,6885
0,6869
0,6884
0,6871
0,6882
0,6873
0,6880
0,6874
0,6878
0,6876
0,6876
0,6876
Efs
2,3002
0,8340
1,5813
0,9710
1,3926
1,0448
1,3044
1,0911
1,2555
1,1215
1,2261
1,1414
1,2083
1,1543
1,1972
1,1626
1,1903
1,1681
1,1858
1,1713
1,1830
1,1737
1,1810
1,1753
1,1798
1,1761
1,1794
1,1765
1,1790
1,1769
1,1786
1,1773
1,1782
1,1777
1,1777
1,1777
δ
13,9172
30,5844
16,7380
25,2923
18,2059
23,3530
19,1170
22,3526
19,7076
21,7676
20,0988
21,4116
20,3509
21,1919
20,5136
21,0547
20,6179
20,9643
20,6860
20,9130
20,7297
20,8748
20,7610
20,8494
20,7799
20,8367
20,7862
20,8304
20,7925
20,8240
20,7988
20,8177
20,8051
20,8114
20,8114
20,8114
Q
0,9928
-0,4134
0,5665
-0,1588
0,3957
-0,0389
0,3025
0,0306
0,2465
0,0740
0,2111
0,1015
0,1890
0,1190
0,1750
0,1300
0,1662
0,1374
0,1605
0,1416
0,1568
0,1448
0,1542
0,1468
0,1526
0,1479
0,1521
0,1484
0,1516
0,1489
0,1510
0,1495
0,1505
0,1500
0,1500
0,1500
Ie
1,1600
0,7286
0,8252
0,6207
0,7187
0,6013
0,6719
0,6008
0,6486
0,6045
0,6361
0,6085
0,6291
0,6117
0,6250
0,6139
0,6226
0,6155
0,6211
0,6165
0,6201
0,6172
0,6195
0,6177
0,6191
0,6180
0,6190
0,6181
0,6188
0,6182
0,6187
0,6183
0,6186
0,6185
0,6185
0,6185
Φ
-58,8532
34,5665
-43,3563
14,8260
-33,4050
3,7118
-26,7529
-2,9159
-22,3315
-7,0311
-19,3843
-9,6048
-17,4864
-11,2151
-16,2636
-12,2283
-15,4821
-12,8983
-14,9719
-13,2790
-14,6455
-13,5635
-14,4115
-13,7527
-14,2708
-13,8471
-14,2238
-13,8943
-14,1768
-13,9415
-14,1298
-13,9886
-14,0827
-14,0357
-14,0357
-14,0357
Eq
1,1368
0,8533
1,0649
0,9211
1,0344
0,9484
1,0172
0,9633
1,0066
0,9724
0,9998
0,9780
0,9955
0,9815
0,9927
0,9838
0,9910
0,9853
0,9898
0,9861
0,9891
0,9867
0,9886
0,9871
0,9883
0,9873
0,9882
0,9874
0,9881
0,9876
0,9880
0,9877
0,9879
0,9878
0,9878
0,9878
Se evidencia que a partir de la iteración numero 34 el procedimiento converge a una solución única
Respuesta: El angulo de carga es de 20,8114 grados con Q=0,15 pu
Sat out
2,758
1,455
2,369
1,652
2,202
1,763
2,108
1,832
2,051
1,876
2,015
1,904
1,993
1,921
1,979
1,932
1,969
1,940
1,964
1,944
1,960
1,948
1,957
1,950
1,956
1,950
1,955
1,951
1,954
1,952
1,954
1,952
1,953
1,953
1,953
1,953
Convergencia del metodo
2,790
2,590
2,390
saturacion
2,190
1,990
1,790
1,590
1,390
1,190
0,990
1
3
5
7
9
11 13 15 17 19 21 23 25 27 29 31 33 35
3. Dibuje los lugares geométricos de las potencias activa y reactiva, corriente de armadura y fuerza
electromotriz del campo a tensión nominal.
Para la resolución de este problema se sigue el mismo procedimiento utilizado en el primer apartado con la
diferencia que ahora se realiza para el punto nominal
%Datos segun el enunciado
Vn=1;
Xd=1.2;
Xq=0.7;
Xsig=0.15;
ifn=300;
S=100;
fpn=0.77;
%Punto nominal
Sn=(1*fpn)+(1i*sin(acos(fpn)));
In=conj(Sn/Vn);
Resultados:
Eq =1.0671
s =2.3760
Xds =0.5919
Efs =1.4501
ifmax=1.7226
(pu)
(pu)
(pu)
(pu)
D=1.4466 + 0.5390i
Id =0.8667
(pu)
(pu)
delta =0.3567
Fin=-0.6920;
(rad)
(rad)
Se hallara el lugar geométrico de la maquina sincronica de polos salientes mediante modificación del algoritmo
numero 10 del libro de texto del curso considerando saturación.
% Tensión, corriente y potencia nominal
Vn=1;
In=1;
Sn=1.;
% Factor de potencia nominal
CosFin=0.77;
% Reactancia del eje directo y cuadratura
Xds=0.5919; Xq=0.7;
% Vector de posibles fp de operación
Fi=(0:-.001:-2)*pi;
% Vector de corrientes de armadura
Ie=In*(cos(Fi)+1i*sin(Fi));
%vector de Potencia aparente
S=conj(Ie/Vn);
% Vector de fasores D para cada corriente
D=Vn+(1i*Xq*Ie);
% Vector de ángulos de carga para cada Ie
delta = atan2(imag(D),real(D));
% Cálculo de la corriente Id
Id=In*sin(delta-Fi).*(sin(delta)-1i*cos(delta));
% Cálculo de la fuerza electromotriz
Efs=D+(1i*((Xds-Xq).*Id));
% Angulo del factor de potencia nominal
Fin = acos(CosFin);
% Fasor de la corriente nominal
Iex = In*(cos(Fin)-1i*sin(Fin));
% Fasor D para la condición nominal
Dx = Vn+ (1i*Xq*Iex);
% Angulo de carga nominal
deltax = atan (imag(Dx)/real(Dx));
% Corriente directa nominal
Idx = In*sin(deltax+Fin).*(sin(deltax)-1i*cos(deltax));
% Fasor de la fuerza electromotriz máxima
Efx = Dx + 1i*(Xds-Xq).*Idx;
% Magnitud de la fuerza electromotriz máxima
Efmax = abs(Efx)*(cos(Fi)+1i*sin(Fi));
% Definición de ejes cuadrados para el gráfico
axis('square');
% Lugar geométrico de la fem (S=cte)
plot (Efs),hold on;
% Lugar geométrico de la pot. aparente const.
plot (Ie);
% Lugar geométrico de la fem máxima
plot(Efmax), hold off;
Diagrama de circulo de la maquina sincronica considerando saturación para el punto nominal
En el diagrama se ven claramente las curvas que representan la corriente de armadura, la tensión máxima del campo
y la tensión del campo para cada factor de potencia con potencia aparente constante.