Solución de los ejercicios del tema 7

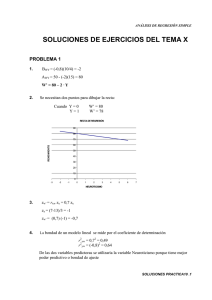
TEMA 7. REGRESIÓN LINEAL
SOLUCIONES DE EJERCICIOS DEL TEMA VII
PROBLEMA 1
1.
Bwy = (-0,8)(10/4) = -2
Awy = 50 - (-2)(15) = 80
W’ = 80 – 2 · Y
2.
Se necesitan dos puntos para dibujar la recta:
Si Y = 0 entonces W’ = 80
Si Y = 2 entonces W’ = 76
RECTA DE REGRESIÓN
90
80
70
RENDIMIENTO
60
50
40
30
20
10
0
-3
-2
-1
0
1
2
3
4
5
6
7
NEUROTICISMO
3.
zw’ = rxw · zx = 0,70 · zx
zx = (7-13)/3 = -1
zw’ = (0,70) (-1) = -0,70
4.
La bondad de un modelo lineal se mide por el coeficiente de determinación
r2xw = 0,702 = 0,49
r2yw = (-0,80)2 = 0,64
De las dos variables predictoras se utilizaría la variable Neuroticismo porque tiene mejor
capacidad predictiva o bondad de ajuste
Soluciones a Ejercicios del Tema 7
TEMA 7. REGRESIÓN LINEAL
PROBLEMA 2
1.
El dato que nos da el problema es el pronóstico en puntuaciones típicas en Aptitudes (P) a
partir de una puntuación típica en Rigidez (R)
zp’ = rpr . zr
-1,2 = rpr · 1,5
rpr = (-1,2)/1,5 = -0,80
Si
rpr = -0,80 = Spr / (Sp·Sr) = Spr / (3)(4)
Entonces
Spr = (-0,80)(3)(4) = -9,6
Según lo anterior, la matriz de varianzas-covarianzas, S, será:
P
R
P
9
-9,6
R
-9,6
16
2.
Bpr = rpr (Sp / Sr) = (-0,80) (4 / 3) = -1,07
Apr = 80 – (-1,07)(20) = 101,4
P’ = 101,4 – 1,07 · R = 101,4 – (1,07)(18) = 81,96
3.
El modelo es apropiado porque su poder predictivo es r2pr = (-0,80)2 = 0,64
4.
La varianza del criterio (S2p) es 16
r2pr = S2p’ / S2p; (-0,80)2 = S2p’ / 16
Despejando S2p’ = (0,64)(16)= 10,24
Si la varianza asociada es 10,24, la varianza error será : 16 – 10,24 = 5,76
Por tanto la descomposición de la varianza del criterio es:
16 = 10,24 + 5,76
Soluciones a Ejercicios del Tema 7
TEMA 7. REGRESIÓN LINEAL
PROBLEMA 3
1.
Media total:
XT 
2.
(200)(100)  (300)(70)
 82
200  300
El problema se refiere a una escala derivada:
zx 
65  60
 0,417
144
T = 10·zx + 50 = 54,17
3.
Se elegirá aquella variable que tenga mayor poder predictivo o mayor bondad
Se elige, por tanto, la variable CV ya que (r2isi,cv = -0,802 = 0,64) > (r2isi,lc = 0,502 = 0,25)
risi , lc 
risi , c v 
150
 0, 5 0
625 144
40
  0, 8 0
625 4
Utilizando CV como variable predictora :
Bisi,cv = (-0,8) (25 / 2) = -10
Aisi,cv = 100 - (-10)(8) = 180
ISI’ = 180 + 10 · CV
4.
Varianza del criterio = S2isi = 625
Varianza común = (r2isi,cv)(S2isi) = (-0,80)2(625) = 400
Varianza error = varianza total – varianza común = 625 – 400 = 225
Por tanto: 625 = 400 + 225
Soluciones a Ejercicios del Tema 7
TEMA 7. REGRESIÓN LINEAL
5.
En la matriz de varianzas-covarianzas del grupo de Normales, la covarianza entre
ansiedad y la variable de observación es –42
La correlación entre ambas variables será: risi ,cv 
6.
42
 0, 70
400 9
Los datos confirman las expectativas de los autores que esperaban una correlación
negativa entre ambas variables (risi,cv = -0,80)
PREGUNTAS TEÓRICAS
1.
1.1
-0,802 = 0,64) > (r2cy = 0,702 = 0,49) > (r2by =0,602 = 0,36)
De mayor a menor bondad, el orden de las variables es A, C y B.
(r
2
ay =
1.2
Según el enunciado, el 51% de la varianza NO está explicada. Por tanto:
... la proporción de varianza NO explicada es 0,51
... la proporción de varianza explicada es 0,49
Luego r2 = 0,49 y
r  0,49  0,7
2.
2.1
Se eliminaría la variable I porque su bondad de ajuste (r2si = 0,202 = 0,04) es la menor
2.2
r2si = 0,202 = 0,04
r2sh = 0,602 = 0,36
r2st = (-0,70)2 = 0,49
3.
3.1.
3.2.
3.3
En puntuaciones directas el origen de la recta puede ser = 0, luego la afirmación es
verdadera
En diferenciales, el origen es 0, luego la afirmación es verdadera
En puntuaciones típicas, la pendiente es el coeficiente de correlación de Pearson, que
nunca puede tomar valores superiores a 1; luego la afirmación es falsa
4.
La alternativa correcta es la C
Soluciones a Ejercicios del Tema 7