Voy a intentar explicar el proceso paso a paso. Para representar

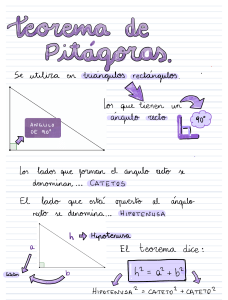
Voy a intentar explicar el proceso paso a paso.
Para representar números irracionales como las raíces que no tienen solución exacta, usamos el teorema de Pitágoras.
El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos, luego la hipotenusa es igual a la raíz
cuadrada de la suma de los cuadrados de los catetos.
=
+
=√
+
Si yo quiero representar la medida de √2, puedo dibujar un tirángulo rectángulo cuyos catetos midan 1.
= √1 + 1 = √2 . La hipotenusa de ese triángulo rectángulo medirá exactamente √2.
Si ahora dibujo una circunferencia con el centro en el vértice inferior de la hipotenusa y tomo como radio la
hipotenusa, cualquier radio de esa circunferencia tendrá la misma medida de la hipotenusa, es decir, el radio de esa
circunferencia medirá √2. Por tanto, el punto donde esa circunferencia corte la recta será la representación gráfica de
√2.
Para representar cualquier raíz no exacta, seguiremos el mismo proceso.
Vamos a representar √3. Tenemos que encontrar dos números de forma que si sumamos sus cuadrados obtenemos 3.
Esos números son 1 y √2. 1 + √2
= 1 + 2 = 3. Luego las medidas de los catetos serán 1 y √2.
Para representar √5, las medidas de los catetos pueden ser 2 y 1.√2 + 1 = √4 + 1 = √5