Funciones Booleanas

1
Capítulo 1
Funciones Booleanas
Cada salida de un sistema digital combinacional puede describirse por una función booleana
de sus variables de entrada. Es decir, las salidas de una red combinacional dependen solamente
de sus entradas. Lo anterior se considera la definición de un sistema digital combinacional.
1.1. Definiciones
i)
Una variable booleana es un símbolo, el cual puede ser sustituido por un elemento del
conjunto B={0,1}. Una constante booleana es un valor perteneciente al conjunto {0,1}.
ii) El elemento que es sustituido por el símbolo de la variable se llama el valor de la variable.
iii) Una función booleana de n variables f ( x1 , x2 ,..., xn ) , es un mapeo o correspondencia que
asocia un valor booleano a f, con cada una de las posibles combinaciones de valores que
pueden tomar las variables.
iv) Una expresión o fórmula booleana queda definida, recursivamente, por las reglas:
a) Constantes y variables son expresiones.
b) Si x e y son expresiones, entonces:
x+y, x·y, x’, y’, (x) también son expresiones.
v) Una función booleana es una función f ( x1 , x2 ,..., xn ) , para la cual existe una expresión
E ( x1 , x2 ,..., xn ) , tal que:
f ( x1 , x2 ,..., xn )
(1.1)
E ( x1 , x2 ,..., xn )
vi) Un literal es el símbolo empleado para una variable o su complemento.
vii) Dos expresiones son equivalentes si una puede ser obtenida a partir de la otra mediante un
número finito de aplicaciones de los postulados o teoremas. O bien si tienen las mismas tablas
de verdad.
viii) Suelen emplearse dos tipos restringidos de expresiones:
La siguiente sintaxis, muestra la formación de expresiones como suma de productos.
Una expresión es un OR de sus términos.
Un término es el AND de sus factores.
Un factor es: una constante, o una variable, o una variable complementada.
Profesor Leopoldo Silva Bijit
19-01-2010
2
Sistemas Digitales
Ejemplo:
0 + a + 1bc + d’ + a’cde
La siguiente sintaxis, muestra la formación de expresiones como producto de sumas.
Una expresión es un AND de sus términos entre paréntesis.
Un término es el OR de sus factores.
Un factor es: una constante, o una variable, o una variable complementada.
Ejemplo: a(1)(c+d’+0)(a + b + c + e’)
1.2. Espacios y funciones Booleanas.
Si definimos el espacio booleano según: B = {0, 1}.
Mediante el producto cartesiano podemos definir el espacio B2, según:
B2 = {0, 1}X{0, 1} = {(00), (01), (10), (11)}
(1.2)
Para x = (x1, x2), podemos definir una función booleana f de dos variables según:
f ( x) : B 2
(1.3)
B
Cada punto de B2 se mapea a B.
Para n variables booleanas, con: x
( x1 , x2 ,..., xn ) , se define una función f según:
f ( x) : B n
(1.4)
B
Para cada punto de B n la función f ( x) asigna un elemento de B ; la función booleana
puede tomar valores 1 ó 0 dependiendo de los valores individuales de las variables.
El conjunto uno u “on” de f puede definirse como los puntos de B n que se mapean a 1:
f1
f
1
(1)
x | f ( x)
1
(1.5)
El conjunto cero u “off” de f puede definirse como los puntos de B n que se mapean a 0:
f0
Si f 1
f
1
(0)
x | f ( x)
0
(1.6)
B n se dice que f es una tautología. Se anota: f 1
B n se tiene que f 1 es vacío y se dice que f no es satisfacible. En lógica la
Si f 0
expresión asociada a la función se denomina contradicción.
Profesor Leopoldo Silva Bijit
19-01-2010
Capítulo 1. Funciones Booleanas
3
Una función es satisfacible cuando existe al menos un elemento en el conjunto uno. Es
decir: para al menos una combinación de las entradas la función toma valor verdadero.
Dos funciones f y g son equivalentes si para todo x
f ( x)
B n se tiene:
(1.7)
g ( x)
1.3. Representación de Funciones Booleanas
1.3.1. Expresiones.
Una función puede ser descrita por una expresión.
Ejemplo:
f( A, B, C) = AB + A’C + AC’
(1.8)
La función puede evaluarse para las diferentes combinaciones de valores que tomen las
variables. Se ilustra la evaluación de la función para A = 1, B = 0 y C = 0.
f( 1, 0, 0)
= 1 0 + 1’ 0 + 1 0’
= 0 +0 0+1 1
= 1
Existen infinitas representaciones equivalentes de una función a través de expresiones.
Esto nos lleva al problema de síntesis lógica que consiste en encontrar la “mejor” expresión
para representar a una función.
La mayor ventaja de esta representación es que puede ser muy compacta y facilita la
manipulación matemática. Sin embargo resulta difícil el tratamiento algorítmico.
1.3.2. Tabla de verdad
Una función puede ser descrita por una tabla de verdad.
Una tabla de verdad despliega todas las posibles combinaciones de valores de las variables y
el valor asociado de la función. Por ejemplo, para la expresión (1.8):
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
C
0
1
0
1
0
1
0
1
f
0
1
0
1
1
0
1
1
Figura 1.1. Tabla de verdad de AB + A’C + AC’.
Profesor Leopoldo Silva Bijit
19-01-2010
4
Sistemas Digitales
La mayor ventaja de la representación por tabla de verdad es que es única. Dos funciones
con tablas de verdad iguales son equivalentes.
Sin embargo a medida que el número de variables aumenta su uso se torna impracticable. El
crecimiento exponencial del número de renglones, ya que éstos se duplican al aumentar en una
variable, impiden que esta representación se emplee para desarrollar algoritmos
computacionales eficientes.
Una variante de las tablas de verdad son las matrices de cobertura que se desarrollan en
4.6.4.
1.3.3. Esquema Lógico.
Un diagrama o esquemático empleando símbolos estandarizados para las funciones lógicas.
Símbolos de compuertas básicas (gates)
NOT
NAND
AND
Q
D
OR
NOR
XOR
XNOR
clk
Figura 1.2. Símbolos lógicos de compuertas y flip-flop D.
Los símbolos lógicos anteriores representan a las funciones booleanas básicas, cuyas
definiciones se presentan en 1.4.2.
La Figura 1.3 ilustra las relaciones geométricas de los símbolos IEEE para las compuertas
lógicas elementales.
26
19
26
5
10
13
4
26
26
Figura 1.3. Relaciones métricas de los símbolos lógicos.
Profesor Leopoldo Silva Bijit
19-01-2010
Capítulo 1. Funciones Booleanas
5
Se ha agregado el símbolo de un elemento que permite almacenar un bit de información; el
cual tiene una señal de entrada D y una señal de salida Q; cuando la señal de control, o reloj clk,
sube a uno se copia o almacena el valor lógico de entrada en el flip-flop. Cuando el control clk,
baja a cero, la salida mantiene el valor almacenado, independientemente de los cambios de la
entrada. Las redes combinacionales se pueden representar sin emplear flip-flops.
Esquemático red digital.
La Figura 1.4 representa mediante símbolos normalizados a la tabla de la Figura 1.1.
A
B
A’
C
A
C’
f
Figura 1.4. Esquemático de AB + A’C + AC’
Existen múltiples esquemáticos que pueden representar la misma función. La ventaja de esta
representación es que está asociada a la implementación.
La mayoría de las herramientas de ayuda al diseño digital permiten ingresar, en un ambiente
visual, un esquemático mediante la colocación de componentes y una posterior interconexión o
alambrado.
Los esquemáticos pueden describirse mediante secuencias de texto, que especifican las
compuertas y los cables que las interconectan. Se denominan netlist a estas representaciones.
Síntesis lógica.
El problema de síntesis lógica consiste en encontrar un circuito C(G, A), formado por un
conjunto G de compuertas y flip-flops, y un conjunto A de alambres o elementos orientados que
interconectan las compuertas y flip-flops.
Se denominan secuenciales a los circuitos digitales que contienen flip-flops, compuertas y
lazos de realimentación; y combinacionales a los que sólo contienen compuertas lógicas sin
realimentaciones.
1.3.4. Diagrama Temporal.
Se representa mediante las formas de ondas de las entradas y de las salidas.
Empleando simuladores, pueden obtenerse formas de ondas de las señales. En estos
diagramas pueden observarse los retardos de propagación a través de las compuertas.
Profesor Leopoldo Silva Bijit
19-01-2010
6
Sistemas Digitales
C
B
A
f
0
10
20
30
40
50
60
70
80
90
100
Figura 1.5. Diagrama temporal
Para confeccionar el diagrama temporal de la Figura 1.5, se generaron las ocho
combinaciones posibles para las variables de entrada y se graficó la salida f, de (1.8).
Los cambios de f no están alineados con los cambios de las entradas, debido a que toma
tiempo para que una compuerta cambie su estado. Es similar a una tabla de verdad, pero
horizontal.
Nótese que entre los tiempos 10 y 20, la señal f debería estar en 1 lógico(A=1, C'=1), sin
embargo esto ocurre un poco después (tipo 2 unidades). Esto se debe al retardo de propagación
a través de las compuertas.
También se aprecia, en la gráfica de la Figura 1.5, que la salida tiene una caída a cero, un
poco después del tiempo 40; como se verá después, es una perturbación.
En el tiempo cercano a cero existe un valor no lógico asociado a f, esto es debido a que el
simulador no puede conocer la salida hasta que los valores iniciales se hayan propagado a través
de las compuertas.
Las formas de ondas pueden también visualizarse mediante un analizador lógico, o con un
osciloscopio.
Retardos de propagación.
Existe un retardo entre la salida y la entrada de una compuerta, que se denomina retardo de
propagación.
La Figura 1.6, muestra las formas de ondas a la entrada y salida de un inversor, en las que se
han definido los retardos de propagación (propagation delay) de un canto de subida y de un
canto de bajada. Al mismo tiempo se definen los tiempos de subida y de bajada.
Los retardos de propagación han sido definidos como cotas superiores de retardos entre
entradas válidas y salidas válidas.
Profesor Leopoldo Silva Bijit
19-01-2010
Capítulo 1. Funciones Booleanas
7
Vin
VIH
VIL
Vout
tPDHL
tPDLH
t
VOH
VOL
t
tf
tr
Tiempo caída
(fall time)
Tiempo subida
(rise time)
Figura 1.6. Retardos de propagación.
También pueden definirse los mínimos retardos de propagación o tiempos de contaminación
como las cotas mínimas entre entradas inválidas y salidas inválidas.
VIH
Vin
VIL
t
Vout
tCDHL
tCDLH
VOH
VOL
t
Figura 1.7. Tiempos de contaminación.
En la práctica, los fabricantes de dispositivos tienen sus propias definiciones de dichos
tiempos y de la forma de medirlos.
Profesor Leopoldo Silva Bijit
19-01-2010
8
Sistemas Digitales
También existen retardos de propagación de las señales a través de los cables, debido a que
la velocidad de propagación de una onda electromagnética que se apoya en los conductores no
viaja a velocidad infinita. Este retardo, a través de los cables, es despreciable en bajas
frecuencias.
La Figura 1.8, muestra las formas de ondas idealizadas en las entradas y salidas de los
inversores. Nótese que los tiempos de propagación son acumulativos en conexiones en cascada.
A1
A2
A3
A1
A2
A3
Figura 1.8. Retardos idealizados en inversor.
Entonces en la práctica, debido a los retardos de propagación, no puede aplicarse el
postulado de complementariedad en las transiciones de A.
Es decir:
A A 1
A A 0
no son verdaderas, en las transiciones; esto debido a que no es posible generar un
complemento de una variable que cambie simultáneamente con la variable.
En diseño de redes combinacionales se asume que si se conoce A; y si se necesita A negada,
ésta se obtendrá mediante un inversor, en este caso A’ estará atrasada en el tiempo respecto de
A. También puede ocurrir que se genere A a partir de A'.
Perturbaciones.
En el diagrama de la Figura 1.9 se muestran perturbaciones, cuando una señal y su
complemento pasan por diferentes compuertas. Se ilustra el caso de and, or, nand y nor.
Se muestran los cambios cuando la señal está retrasada y adelantada con respecto a su
complemento.
Profesor Leopoldo Silva Bijit
19-01-2010
Capítulo 1. Funciones Booleanas
A
9
A’
A’
A
A
A’
A’
A
A
A’
A
A’
A
A’
A
A’
A' atrasada respecto de A. A atrasada respecto de A'
Figura 1.9. Perturbaciones estáticas en compuertas.
Se denomina perturbación en 1, si el nivel de la salida debe permanecer en 1 y si se produce
momentáneamente un cero. La duración y ocurrencia de la perturbación depende de los retardos
de las señales que la producen.
Se tiene una perturbación en "0" si existe una subida momentánea del nivel de la señal de
salida a 1, debiendo ésta permanecer baja.
En una compuerta AND, en la que ingresan una señal y su complemento, se produce
perturbación del cero lógico, con el canto de subida de A, si ésta está adelantada respecto de A';
o en el canto de subida de A' si ésta está adelantada respecto de A.
En una compuerta OR, en la que ingresan una señal y su complemento, se produce
perturbación del uno lógico, con el canto de bajada de A, si ésta está adelantada respecto de A';
o en el canto de bajada de A' si ésta está adelantada respecto de A.
1.3.5. Diagramas de Venn.
Similares al visto en el Teorema 13 de consenso, en el Apéndice 1.
Otras formas de representación, que se desarrollaran más adelante, se enumeran a
continuación:
Profesor Leopoldo Silva Bijit
19-01-2010
10
Sistemas Digitales
1.3.6. Mapas de Karnaugh.
Es la principal representación conceptual de funciones booleanas. Se dispone de esta
representación desde el año 1953. Su uso práctico queda limitado a funciones de cinco o menos
variables.
1.3.7. N-cubos.
Diagrama de la función en un espacio discreto multidimensional. Lo emplearemos como
fundamento conceptual de los mapas de Karnaugh y de los métodos de minimización.
1.3.8. Lenguajes de descripción de hardware.
Para sistemas reales se emplean aplicaciones computacionales que emplean lenguajes para la
descripción del hardware (HDL Hardware Description Language).
El empleo de lenguajes como VHDL o Verilog, permiten describir el diseño, efectuar
simulaciones y verificaciones, y finalmente efectuar el proceso de síntesis.
1.4. Funciones de varias variables.
1.4.1 Funciones de n variables.
Si hay n variables, la tabla de verdad tendrá N 2n renglones. Para un renglón
determinado la función puede tomar valor 0 ó 1. Entonces pueden escribirse 2 N tablas de
verdad diferentes.
n
Es decir, 22 funciones booleanas de n variables.
La siguiente tabla muestra el rápido crecimiento del número de funciones booleanas de n
variables.
n
0
1
2
3
4
...
N
2n
1
2
4
8
16
22
n
2
4
16
256
65536
...
Figura 1.10. Número de funciones
El caso n = 0 se interpreta como una función descrita por 0 variables; es decir por una
constante. En esta situación existe sólo un valor posible (N=1) y como la constante puede ser 0
ó 1 el número de funciones de cero variables es 2.
Profesor Leopoldo Silva Bijit
19-01-2010
Capítulo 1. Funciones Booleanas
11
1.4.2 Funciones de dos variables.
Para n = 2 las tablas de verdad tienen cuatro renglones. Los cuatro casilleros de una función
pueden llenarse de 16 formas, las que se muestran en la siguiente tabla.
A
0
0
1
1
B
0
1
0
1
f0
0
0
0
0
f1
1
0
0
0
f2
0
1
0
0
f3
1
1
0
0
f4
0
0
1
0
f5
1
0
1
0
f6
0
1
1
0
f7
1
1
1
0
f8
0
0
0
1
f9
1
0
0
1
f10
0
1
0
1
f11
1
1
0
1
f12
0
0
1
1
f13
1
0
1
1
f14
0
1
1
1
f15
1
1
1
1
Figura 1.11. Funciones de dos variables
Las funciones se han numerado, en binario, considerando el primer renglón como el dígito
menos significativo. Por ejemplo: 0111 equivale a 7, en sistema binario. Lo cual puede verse
de la siguiente relación: 0 23 +1 22 + 1 21 +1 20 = 7
Las 16 funciones booleanas de dos variables pueden representarse en forma analítica,
mediante expresiones booleanas, las que se muestran en la Figura 1.8.
f0 = 0
f1 = A'B' = (A + B)'
f2 = A'B
f3 = A'B' + A'B = A'
f4 = AB'
f5 = A'B' + AB' = B'
f6 = A'B + AB'
f7 = A'B' + A'B + AB' = A' + B' = (AB)'
f8 = AB
f9 = A'B' + AB
f10 = A'B + AB = B
f11 = A'B' + A'B + AB = A' + B
f12 = AB' + AB = A
f13 = A'B' + AB' + AB = A + B'
f14 = A'B + AB' + AB = A + B
f15 = A'B' + A'B + AB' + AB = 1
Figura 1.12. Expresiones para funciones de dos variables
Las diferentes expresiones pueden comprobarse verificando que se satisfacen las tablas de
verdad de la Figura 1.11.
Algunas de estas funciones son tan utilizadas, que se las reconoce con un nombre.
Definiciones de funciones lógicas de dos variables.
f1 (A, B) = nor (A, B) = A
B
f 8 (A, B) = and (A, B) = A B
f 6 (A, B) = xor (A, B) = A
B
(1.9)
f 7 (A, B) = nand (A, B) = A B
f14 (A, B) = or (A, B) = A + B
Profesor Leopoldo Silva Bijit
19-01-2010
12
Sistemas Digitales
La función 1 se denomina nor (por: not or). La función 8 se denomina and; la 14 or; la 3 es la
negación de A, o not A.
La función 6, se denomina xor, por or exclusivo. Toma valor verdadero si los valores lógicos
de A y B son diferentes; por esto también se la denomina desigualdad o diferencia.
La función 9 se denomina xnor. Toma valor verdadero si los valores lógicos de A y B son
iguales. Por esto se la denomina igualdad o coincidencia .
La función 9 se denomina equivalencia lógica o bicondicional; la función 11 es la
implicancia lógica o condicional.
f9 (A,B) = not (xor (A,B)) = A
f11 (A,B) = A
B =A
B
(1.10)
B
En el Apéndice 1, se desarrolla con más detalles la importancia de la función 11 en el cálculo
proposicional.
En la Figura 1.13 se destaca la diferencia entre OR (inclusivo) y XOR (exclusivo), difieren
en el último renglón de su tabla de verdad.
A
0
0
1
1
B
0
1
0
1
OR
0
1
1
1
XOR
0
1
1
0
Figura 1.13. Diferentes or
Propiedades de la función Xor.
A
0=A
A
1 =A
A
A=0
A
A=1
Las primeras dos expresiones se emplean en el cálculo de complementos; se puede generar la
señal o su complemento mediante una señal de control que es una entrada a la compuerta xor.
Las dos últimas se emplean en circuitos para detectar errores.
También se tienen las siguientes equivalencias:
x y=y x
(x y) z = x (y
x (y z)=xy xz
z)
Las que pueden demostrarse empleando tablas de verdad.
Profesor Leopoldo Silva Bijit
19-01-2010
Capítulo 1. Funciones Booleanas
13
Conjuntos Funcionalmente Completos.
Cualquier expresión booleana puede ser escrita mediante los operadores AND, OR, y NOT.
Se dice que estos operadores constituyen un conjunto funcionalmente completo.
Por lo tanto un circuito combinacional puede construirse usando sólo compuertas AND, OR
y NOT.
Las siguientes relaciones muestran que la función NAND es funcionalmente completa, ya
que pueden implementarse circuitos combinacionales sólo empleando este tipo de compuertas.
Si la función efectúa el nand de sus entradas, puede generar:
El not de una variable, ingresando la misma señal en ambas entradas.
El or de dos variables, ingresando las señales complementadas al nand.
El and de dos variables, complementando la salida del nand, mediante un inversor
(implementado también empleando una compuerta nand).
nand ( A, B)
AB
nand ( A, A)
A
nand ( A, B )
A B
También la función NOR es funcionalmente completa. Esto puede verse observando que la
función nor, genera el complemento de una variable, y también el or y el and de dos variables.
nor ( A, B)
A B
nor ( A, A)
A
nor ( A, B )
AB
Generalización para funciones de más de dos variables.
Algunas funciones pueden generalizarse para más de dos variables, por ejemplo:
and (a, b, c) abc
or (a, b, c, d ) a b c d
(1.11)
La función xor para n variables puede generalizarse, estableciendo que la función toma valor
uno si se tiene un número impar de variables que toman valores iguales a 1; y toma valor cero si
el número de variables que toman valor 1 es par.
1.5. Formulación de expresiones booleanas.
A partir de la descripción de un problema, generalmente expresada en forma de texto, se
desea obtener fórmulas lógicas mediante expresiones que emplean variables booleanas.
Profesor Leopoldo Silva Bijit
19-01-2010
14
Sistemas Digitales
Ejemplo 1.1.
(Taub): En un estante hay 5 libros (v, w, x, y, z) que se pueden tomar cumpliendo las
siguientes reglas:
a) Se seleccionan v o w o ambos
b) Se seleccionan x o z pero no ambos
c) se selecciona v y z juntos, o bien una selección que no incluya a ninguno de ellos
d) si se selecciona y, también debe seleccionarse z
e) si se selecciona a w, también debe seleccionarse a v e y.
Expresar cómo seleccionar un grupo de libros cumpliendo las reglas anteriores.
Solución.
Sean:
u la proposición lógica que indica que la selección de libros cumple las reglas
el nombre del libro es la proposición lógica que indica que se tomó dicho libro para formar
la selección.
Como las reglas de selección deben cumplirse simultáneamente, debe entenderse que debe
cumplirse la primera regla y la segunda, y así sucesivamente.
Por lo tanto: u es igual al and de las reglas individuales.
La regla a), establece el or (incluye a ambos) de v con w. Es decir: v + w.
La regla b), establece el xor (no incluye a ambos) de x con z. Es decir: x
z.
Para la regla c), se tiene:
v
0
0
1
1
Es decir: (v
z
0
1
0
1
regla c)
1
0
0
1
z)'
La regla d) traducida es: y
La regla e) traducida es: w
z
vy
Entonces: u = (v + w)( x
z) (v
z)' (y
z)( w
vy )
Reemplazando los operadores por or, and y not, se obtiene:
u = (v + w)(xz' + x'z)(vz + v'z')(y' + z)( w' + vy)
Efectuando los productos:
Profesor Leopoldo Silva Bijit
19-01-2010
Capítulo 1. Funciones Booleanas
15
(v+w) (vz +v'z') = vvz + vv'z + vwz + v'wz' que se simplifica a: vz + v'wz'
(xz' +x'z)(y' +z) = xy'z' + xzz' + x'y'z + x'zz que se simplifica a : xy'z' + x'z
entonces queda: u = (vz + v'wz' )( xy'z' + x'z )( w' + vy)
El producto (vz + v'wz' )( w' + vy) puede simplificarse a: (vw'z + vyz)
Y el producto ( xy'z' + x'z ) (vw'z + vyz) = x'vw'z + x'vyz
Finalmente: u = vx'z(w' +y)
Que puede leerse:
Se debe seleccionar v y z, y rechazar x; y si se selecciona w también debe seleccionarse y.
Una frase alternativa para (w' +y) es: si no se selecciona w, la selección de y es opcional.
Ejemplo 1.2.
(Dietmeyer). Tres interruptores(a, b, c) controlan dos ampolletas (una roja R, y otra verde V)
del modo siguiente:
a) Cuando los tres interruptores están cerrados, se enciende la luz roja.
b) Cuando el interruptor A está abierto y B o C están cerrados se enciende la luz verde.
c) No deben encenderse ambas ampolletas a la vez.
d) En el resto de los casos la roja debe encenderse, excepto cuando los tres interruptores están
abiertos, en este caso no debe encenderse ninguna ampolleta.
Solución:
Se emplea la siguiente asignación de valores lógicos:
a interruptor cerrado se asigna 1 lógico,
a ampolleta encendida se le asigna 1 lógico.
La especificación b) se interpreta como o incluyente; es decir, B o C o ambos cerrados.
De la condición d), se extrae la especificación e)
e) cuando los tres interruptores están abiertos no debe encenderse ninguna ampolleta.
Si se puede completar la tabla de verdad, el problema está completamente especificado:
Profesor Leopoldo Silva Bijit
19-01-2010
16
Sistemas Digitales
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
C
0
1
0
1
0
1
0
1
por condición d
R
0
0
0
0
1
1
1
1
V
0
1
1
1
0
0
0
0
por condición a.
por condición e
por condición b.
por condición c
por condición c
Figura 1.14. Tabla de verdad para Ejemplo 1.2.
Se va completando la tabla, con las especificaciones, la última en aplicar es la d).
Se advierte que si no se hubiese dado, por ejemplo, la especificación c), el problema queda
indeterminado. En estos casos es preciso efectuar suposiciones o agregar especificaciones.
Por esto podría decirse que una tabla de verdad es una especificación formal.
Una vez que se tiene la tabla pueden encontrarse las expresiones para R y V en función de A,
B y C.
Puede comprobarse que cada uno de la función está asociado a un producto lógico de las
variables A, B y C. Y que la función es la suma lógica de esos productos, se tiene entonces que:
R = AB'C' + AB'C + ABC' + ABC
V = A'B'C + A'BC' + A'BC
que pueden simplificarse, empleando teoremas, resultando:
R = A.
V = A'(B +C)
1.6. Teoremas relativos a funciones de varias variables.
T.16 Función Dual
f d ( x1 , x2 ,..., xn , 0,1, •, )
f ( x1 , x2 ,..., xn , 0,1, •, )
(1.12)
Este teorema permite calcular la función dual ( fd) de una función f. Debe notarse que no se
intercambian las constantes y los operadores.
Profesor Leopoldo Silva Bijit
19-01-2010
Capítulo 1. Funciones Booleanas
17
T.17 Reducción.
x1
f ( x1 , x2 ..., xn )
x1
f (0, x2 ,..., xn )
x1
f ( x1 , x2 ..., xn )
x1
f (1, x2 ,..., xn )
(1.13)
Demostración por inducción perfecta de la primera proposición. Se analizan todos los casos
que se presentan cuando la variable x1 toma todos los valores que le son posibles.
Considerando:
x1
Cuando x1 = 0, entonces:
f ( x1 ,..., xn )
0
f (0, x2 ,..., xn )
f (0, x2 ..., xn )
0
f (0, x2 ..., xn )
Resultando por P3 que:
Cuando x1 = 1, entonces:
Resultando por T9 que:
x1
1 f (1, x2 ..., xn )
1
f (0, x2 ,..., xn )
f (0, x2 ,..., xn )
f (0, x2 ,..., xn )
1 = 1
x1
f (0, x2 ,..., xn ) es válida para todos los
Se concluye que: x1 f ( x1 ,..., xn )
valores que puede tomar x1. El postulado P3 y el Teorema 9, se describen en el Apéndice 1.
T.18 Teorema de expansión de Shannon.
f ( x1 , x2 ,..., xn ) x1 f (1, x2 ,..., xn ) x1 f (0, x2 ,..., xn )
f ( x1 , x2 ,..., xn ) ( x1
f (0, x2 ,..., xn )) ( x1
(1.14)
f (1, x2 ,..., xn ))
Las funciones f (0, x2 ,..., xn ) y f (1, x2 ,..., xn ) se denominan cofactores x1 de f, y son
funciones de (n-1) variables.
Demostración por inducción perfecta o completa de la primera proposición.
Considerando: f ( x1 , x2 ,..., xn )
Cuando x1 = 0, entonces:
f ( 0,x2 ,...,x n )
Por T.9 y P.3 se llega a:
x1 f (1, x2 ,..., xn ) x1 f (0, x2 ,..., xn )
0 f ( 1,x2 ,...,x n ) 1 f ( 0,x2 ,...,x n )
f (0, x2 ,..., xn )
f (0, x2 ,..., xn )
Cuando x1 = 1, entonces:
f ( 1,x2 ,...,x n )
Por T.9 y P.3 se llega a:
Profesor Leopoldo Silva Bijit
1 f ( 1,x2 ,...,x n ) 0 f ( 0,x2 ,...,x n )
f (1, x2 ,..., xn )
f (1, x2 ,..., xn )
19-01-2010
18
Sistemas Digitales
Entonces f ( x1 , x2 ,..., xn )
los valores que puede tomar x1.
x1 f (1, x2 ,..., xn ) x1 f (0, x2 ,..., xn ) es válida para todos
La repetida aplicación de este teorema permite representar una función de n variables como
una suma de productos o un producto de sumas.
Ejemplo 1.3.
En desarrollos de minimización se clasifican las funciones, dependiendo de cómo aparecen
las variables en una forma suma de productos.
Si se divide o parte f en términos de x3, se tiene:
f ( x1 , x2 , x3 )
f ( x1 , x2 , 0) x3 ' f ( x1 , x2 ,1) x3
Si f ( x1 , x2 , 0) 0 se dice que f es unata positiva respecto de x3. Es decir si en la forma
suma de productos no aparece x3’.
Si f ( x1 , x2 ,1) 0 se dice que f es unata negativa respecto de x3. Es decir si en la forma
suma de productos no aparece x3.
T.19 Generalización de De Morgan.
f '( x1 , x2 ..., xn , 0,1, , )
f ( x '1 , x '2 ,..., x 'n ,1, 0, , )
1.7. Minimización (reducción o simplificación) de Funciones.
Criterios de Reducción.
Cada función tiene una y sólo una tabla de verdad asociada; sin embargo pueden escribirse
diferentes expresiones booleanas para la misma función. Esto implica diferente costo.
a) Si se minimiza el número de compuertas empleadas, se tendrá un circuito más pequeño, lo
que influencia directamente el costo de manufactura, debido a que se requiere un circuito
impreso de menor superficie y menor número de componentes. También disminuyen las
probabilidades de fallas debidas a componentes defectuosas, debido al menor número de éstas.
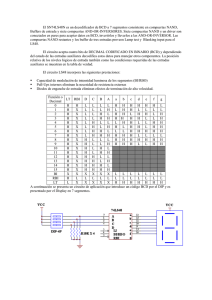
La Figura 1.15, muestra el encapsulamiento de compuertas en pastillas de 14 patas, en
dispositivos de baja integración. Debe notarse que a medida que aumentan las entradas de las
compuertas, disminuye el número de éstas en un chip o pastilla.
Profesor Leopoldo Silva Bijit
19-01-2010
Capítulo 1. Funciones Booleanas
19
Figura 1.15. Compuertas TTL serie 74xx
Al aumentar la densidad de transistores en los dispositivos, el problema es encontrar
metodologías para mapear adecuadamente los diseños basados en compuertas a las estructuras
de los dispositivos programables.
b) Si se minimiza el número de entradas a las compuertas, se tendrá menos transistores en
cada compuerta y por lo tanto un costo menor. Si se considera las señales y sus complementos,
presentes en una expresión, como entradas de compuertas, puede definirse el concepto de literal
en una expresión.
Un literal es la ocurrencia de una variable o su forma complementada en una expresión.
Si se desea minimizar las entradas, debe minimizarse el número de literales en una
expresión.
Ejemplo 1.4.
f(x, y, z) = x’y(z+y’x) +y’z es una expresión que tiene 7 literales.
Puede reducirse, aplicando postulados y teoremas a:
f(x, y, z) = (xy)’z = (x’ +y’)z que tiene 3 literales.
Es usual asumir que se dispone de las variables y sus complementos como entradas de una
red combinacional, por esta razón se cuentan los literales.
Profesor Leopoldo Silva Bijit
19-01-2010
20
Sistemas Digitales
Como se verá más adelante algunos elementos básicos de memoria (flip-flops) entregan
como salidas las variables y sus complementos, en la Figura 1.16 se muestran un flip-flop JK y
un flip-flop D, la señal de control CP (clock pulse) es el reloj:
J Q
K Q
CP _
D Q
_
CP Q
Figura 1.16. Salidas complementadas en Flip-flops
También en los dispositivos programables existen circuitos inversores en las entradas, en la
Figura 1.17., se ilustra la generación de A’ a partir de la entrada A:
A
A'
A
Figura 1.17. Entradas complementadas
Ejemplo 1.5.
Como se ha dicho: Existen diversas expresiones para una misma función.
Sea la función f(A, B, C) = (A+C) B' (C +D)
Que puede implementarse con compuertas según:
A
C
B
f
C
D
Figura 1.18. Diseño en dos niveles.
La representación es en dos niveles. Definiendo el nivel por el número de compuertas a
través de las cuales se propagan las señales de entrada hasta llegar a la señal de salida.
La implementación, de la Figura 1.18, tiene 8 entradas y 5 literales. Y emplea una compuerta
que tiene más de dos entradas (3 en el and del ejemplo).
Si expresamos ahora la misma función f por la expresión equivalente:
Profesor Leopoldo Silva Bijit
19-01-2010
Capítulo 1. Funciones Booleanas
21
f =(A+C)(B' (C + D))
De este modo todas las compuertas empleadas no tienen más de dos entradas, según puede
verse en el esquema de la Figura 1.19:
A
C
f
B
C
D
Figura 1.19. Diseño en tres niveles.
La implementación de la Figura 1.19 tiene 9 entradas y 5 literales. La suma de las entradas se
obtiene sumando las entradas a todas las compuertas, ya sea en el diagrama o en la expresión
booleana.
Notando que un cambio en la señal C o D o B, debe propagarse por tres compuertas, se dice
que el circuito está implementado en tres niveles. La señal A se propaga en dos niveles hasta la
salida f.
c) Si lo que se desea es aumentar la velocidad de respuesta, se requiere disminuir el número de
niveles.
Para lograr esto, en general se requerirán compuertas con mayor número de entradas lo cual
aumenta el costo.
Obviamente existirá un compromiso entre velocidad y costo; el que se suele denominar
compromiso: tiempo-espacio.
Los circuitos lógicos que tienen igual tabla de verdad son equivalentes, pero pueden tener
diferente costo, en tiempo o en espacio.
Existen diversas herramientas para explorar el compromiso entre retardos y tamaño, que
permiten generar automáticamente diferentes soluciones, empleando minimización lógica para
reducir la complejidad espacial y optimización de los retardos para aumentar la velocidad de
respuesta.
Profesor Leopoldo Silva Bijit
19-01-2010
22
Sistemas Digitales
Índice general.
CAPÍTULO 1.........................................................................................................................................1
FUNCIONES BOOLEANAS ...............................................................................................................1
1.1. DEFINICIONES ...............................................................................................................................1
1.2. ESPACIOS Y FUNCIONES BOOLEANAS............................................................................................2
1.3. REPRESENTACIÓN DE FUNCIONES BOOLEANAS ............................................................................3
1.3.1. Expresiones. .........................................................................................................................3
1.3.2. Tabla de verdad ....................................................................................................................3
1.3.3. Esquema Lógico. ..................................................................................................................4
Símbolos de compuertas básicas (gates) .................................................................................................... 4
Esquemático red digital.............................................................................................................................. 5
Síntesis lógica. ........................................................................................................................................... 5
1.3.4. Diagrama Temporal. ............................................................................................................5
Retardos de propagación. ........................................................................................................................... 6
Perturbaciones............................................................................................................................................ 8
1.3.5. Diagramas de Venn. .............................................................................................................9
1.3.6. Mapas de Karnaugh. ..........................................................................................................10
1.3.7. N-cubos...............................................................................................................................10
1.3.8. Lenguajes de descripción de hardware. .............................................................................10
1.4. FUNCIONES DE VARIAS VARIABLES. ............................................................................................10
1.4.1 Funciones de n variables. ....................................................................................................10
1.4.2 Funciones de dos variables. ................................................................................................11
Definiciones de funciones lógicas de dos variables. ................................................................................ 11
Conjuntos Funcionalmente Completos. ................................................................................................... 13
Generalización para funciones de más de dos variables........................................................................... 13
1.5. FORMULACIÓN DE EXPRESIONES BOOLEANAS.............................................................................13
Ejemplo 1.1. .................................................................................................................................14
Ejemplo 1.2. .................................................................................................................................15
1.6. TEOREMAS RELATIVOS A FUNCIONES DE VARIAS VARIABLES. ....................................................16
T.16 Función Dual .......................................................................................................................16
T.17 Reducción. ............................................................................................................................17
T.18 Teorema de expansión de Shannon. .....................................................................................17
Ejemplo 1.3. ............................................................................................................................................. 18
1.7. MINIMIZACIÓN (REDUCCIÓN O SIMPLIFICACIÓN) DE FUNCIONES. ...............................................18
Criterios de Reducción. ................................................................................................................18
Ejemplo 1.4. .................................................................................................................................19
Ejemplo 1.5. .................................................................................................................................20
ÍNDICE GENERAL. ..............................................................................................................................22
ÍNDICE DE FIGURAS ...........................................................................................................................23
Profesor Leopoldo Silva Bijit
19-01-2010
Capítulo 1. Funciones Booleanas
23
Índice de Figuras
Figura 1.1. Tabla de verdad de AB + A’C + AC’. ........................................................................ 3
Figura 1.2. Símbolos lógicos de compuertas y flip-flop D............................................................ 4
Figura 1.3. Relaciones métricas de los símbolos lógicos. ............................................................. 4
Figura 1.4. Esquemático de AB + A’C + AC’ .............................................................................. 5
Figura 1.5. Diagrama temporal...................................................................................................... 6
Figura 1.6. Retardos de propagación. ............................................................................................ 7
Figura 1.7. Tiempos de contaminación. ........................................................................................ 7
Figura 1.8. Retardos idealizados en inversor................................................................................. 8
Figura 1.9. Perturbaciones estáticas en compuertas. ..................................................................... 9
Figura 1.10. Número de funciones .............................................................................................. 10
Figura 1.11. Funciones de dos variables ..................................................................................... 11
Figura 1.12. Expresiones para funciones de dos variables .......................................................... 11
Figura 1.13. Diferentes or............................................................................................................ 12
Figura 1.14. Tabla de verdad para Ejemplo 1.2. ......................................................................... 16
Figura 1.15. Compuertas TTL serie 74xx ................................................................................... 19
Figura 1.16. Salidas complementadas en Flip-flops .................................................................... 20
Figura 1.17. Entradas complementadas ....................................................................................... 20
Figura 1.18. Diseño en dos niveles.............................................................................................. 20
Figura 1.19. Diseño en tres niveles. ............................................................................................ 21
Profesor Leopoldo Silva Bijit
19-01-2010