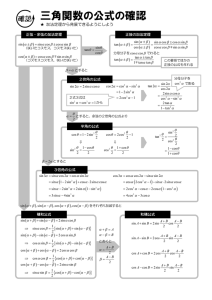
θ = θ + = cos α β sin α β tan α β

Instructor:
Chris King
I.
Math 127
Test 2 Review
Use a calculator to solve the equation on the interval [0, 2π). Round the answer
to two decimal places.
1. tan θ = 5
II.
2. 4 cos θ + 3 =
0
Solve the equation on the interval [0, 2π).
2. 1 + sin θ =
2 cos 2 θ
1. tan θ = 2sin θ
III.
Solve each. Find all solutions.
0
1. sin 2 x − sin x =
IV.
2. cos 4 x =
Find the exact value under the given conditions.
π
15
,0 < α < ;
17
2
a. Find cos (α + β )
1. sin α=
cos β=
π
3
,0 < β <
5
2
b. Find sin 2 β
a
c. Find tan
2
12
3π
,π < a <
;
5
2
a. Find sin (α + β )
2. tan a
=
cos =
β
−8 π
, < β <π
17 2
b. Find tan 2a
β
c. Find sin
2
−5 π
15 π
, < α < π ; sin=
β
, < β <π
13 2
17 2
a. Find tan (a + β )
3. cos=
α
b. Find cos 2 β
α
c. Find cos
2
− 2
2
III. Verify the identities.
1. ( 4sin u cos u ) (1 − 2sin 2 u ) =
sin 4u
2.
3.
4.
5.
6.
cos θ − cos 5θ
= tan 2θ
sin θ + sin 5θ
cos 4 θ − sin 4 θ =
cos 2θ
cot α cot β − 1
cot (α + β ) =
cot α + cot β
csc 2 θ
sec ( 2θ ) =
csc 2 θ − 2
cos ( x − y ) 1 + tan x tan y
=
cos ( x + y ) 1 − tan x tan y
7. 1. sin θ csc θ − cos 2 θ =
sin 2 θ
8. 3sin 2 θ + 4 cos 2 θ =
3 + cos 2 θ
sec θ sin θ
9.
2 tan θ
+
=
csc θ cos θ
sin θ cos θ
tan θ
10.
=
2
2
cos θ − sin θ 1 − tan 2 θ