Soto está encargado de patear un tiro libre a 25 metros de la

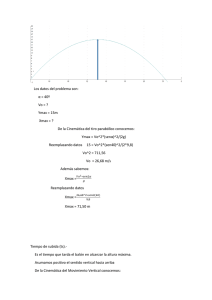
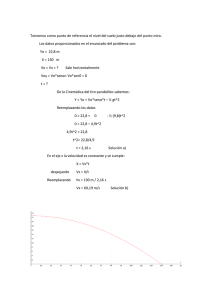
Soto está encargado de patear un tiro libre a 25 metros de la portería. La barrera se para a los
9.15 metros y tienen una altura promedio de 1.85 metros. La altura del arco del fútbol es de
2.50 metros. Si patea el balón con una velocidad de 75 km/h con un ángulo de 50° sobre la
horizontal, habrá posibilidad de gol?
Los datos son:
Vo = 75 Km/h
75Km/h(1000m/1Km)(1h/3600s) = 20,83 m/s
α= 50º
Sabemos por Cinemática del tiro parabólico que la ecuación de la trayectoria es:
y = x.tgα- ½ g.x^2/(Vo.cosα)^2
Remplazando en dicha ecuación los datos para:
X = 9,15m
y = (9,15)(tg50) - ½ (9,8)(9,15)^2/(20,83*cos50)^2
Y = 8,62 m
Es decir a 8,62m – 1,85m = 6,77m sobre la barrera humana
X = 25 m
y = (25)(tg50) - ½ (9,8)(25)^2/(20,83*cos50)^2
Y =12,71m
Es decir a 12,71m – 2,50m = 10,21m sobre la portería
En esas condiciones no es posible hacer un gol, a menos que se disminuya el ángulo de tiro o
la velocidad inicial del balón
A continuación detallo la demostración de la ecuación de la trayectoria:
La ecuación de la trayectoria es la ecuación que nos permite calcular la altura de un cuerpo
“y” que sigue una trayectoria parabólica en función de su avance horizontal “x”.
De la Cinemática del movimiento vertical conocemos:
y = Vo.senα.t – ½ gt^2
(1)
En el eje x el movimiento es uniforme:
X = Vo.cosα.t
Despejando
t = 𝑥/(𝑉𝑜. 𝑐𝑜𝑠𝛼)
(2)
Reemplazando (2) en (1)
y = Vo.senα.x/(Vo.cosα) – ½ g((𝑥/(𝑉𝑜. 𝑐𝑜𝑠𝑎))^2
y = x.tgα- ½ g.x^2/(Vo.cosα)^2
(3)