FormEuler

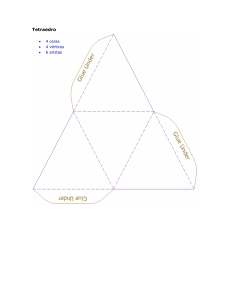
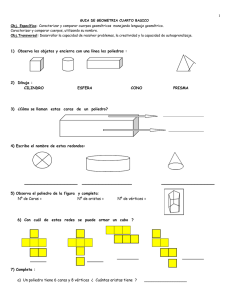
FÓRMULA DE EULER
Leonhard Euler. (1707-1783)
Matemático suizo.
A pesar de la pérdida de un ojo y una ceguera
creciente, Euler dedicó cerca de 900 artículos a las
matemáticas, la música, la mecánica, la astronomía, la
óptica, la ciencia naval, etc.
Fue uno de los principales artífices del auge del
análisis matemático en el s. XVIII.
En la figura siguiente tienes pintado un
poliedro. En él se te indican algunos elementos
característicos.
1. Define cada uno de estos elementos.
cara:
vértice:
arista:
2. ¿Cuántas caras, vértices y aristas tiene este poliedro?
caras:
vértices:
aristas:
3. ¿Cuántas caras se habrán de juntar en un vértice como mínimo?
4. ¿Cuánto pueden sumar los ángulos de las caras que concurren en un mismo
vértice como máximo?
FÓRMULA DE EULER
En los cinco poliedros regulares cuenta el número
de caras, vértices y aristas y escríbelos en la tabla.
1
5. ¿Encuentras alguna relación entre C, V y A?
6. Completa la frase y escribe la fórmula. En todos los poliedros regulares se
verifica siempre que el número de caras más el número de vértices es igual al
número de aristas ………………….
C + V = A ……………
7. ¿Es cierta esta fórmula también para los poliedros no regulares?
8. ¿Qué pasa cuando hacemos un 9. ¿Y se le añadimos un prisma de base
corte en la esquina de un cubo?
cuadrada a una cara?
10. En los cuatro poliedros siguientes cuenta el número de caras, vértices y
aristas:
11. ¿Crees que la fórmula de Euler es cierta para cualquier poliedro?
12. ¿También se cumple en estos
dos?
13. Enuncia la (definitiva) fórmula
de Euler:
2
14. En la tabla siguiente se dan algunos datos de poliedros convexos. Complétala
e intenta dibujar alguno de ellos.
Poliedro
C
1
4
2
3
V
6
8
5
A
12
6
15. Un poliedro tiene 7 caras. Cuatro de ellas son pentágonos y tres cuadriláteros.
¿Cuántas aristas tiene?
¿Cuántos vértices tiene?
16. Un poliedro tiene dos caras hexagonales y todas las demás son triángulos. Llamamos t al
número de caras triangulares.
a) Escribe una expresión para el número de aristas del poliedro.
b) Usa la fórmula de Euler para una expresión del número de vértices.
3