Productos Notables

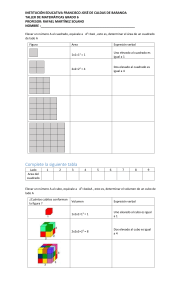
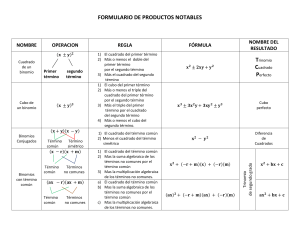
Productos Notables
Dentro de la multiplicación algebraica existen algunos productos que pueden ser
desarrollados en forma directa, es decir sin multiplicar término a término y luego reducir.
Son multiplicaciones de polinomios, en los cuales se repiten uno o más términos lo que
permite establecer ciertas reglas fijas para obtener el producto, por simple inspección, esto es, sin
necesidad aplicar propiedad distributiva ni reducir términos semejantes.
Suma por diferencia.Es igual a la diferencia de los cuadrados de los términos, es decir:
(𝑎 + 𝑏)(𝑎 − 𝑏) = 𝑎2 − 𝑏 2
Ejemplos:
(1) (a – 4) (a + 4) = a2 - 16.
(2) (3a + 2b) (3a – 2b) = 9a2 - 4b2.
(3) (x2 + y3) (x2 – y3) = x4 – y6.
Cuadrado de Binomio.El desarrollo de este producto corresponde al cuadrado del primer término, más (o menos)
el doble del producto del primer término por el segundo y más el cuadrado del segundo, es decir:
(𝑎 ± 𝑏)2 = 𝑎2 ± 2𝑎𝑏 + 𝑏 2
Ejemplo:
(1) (x + 4)2
= x2 + 8x + 16.
2
(2) (5x – 4)
= 25x2 – 40x + 16.
2
3 2
(3) (3a + 2b ) = 9a4 + 12a2b3 + 4b6.
Ejercicios.- Desarrolla los siguientes cuadrados de binomios por simple inspección.
Ejercicios.- Desarrolla por simple inspección las siguientes sumas por diferencias.
Producto de Binomios con un Término en Común.
Es el cuadrado del término común, más el producto del término común por la suma de los
términos no comunes y más el producto de de los términos no comunes.
Cubo de Un Binomio.Corresponde al cubo del primer Término, más (o menos) el triple del cuadrado del primer término
multiplicado por el segundo, más el triple del primer término multiplicado por el cuadrado del
segundo y más (o menos) el cubo del segundo término, es decir:
(𝑎 ± 𝑏)3 = 𝑎3 ± 3𝑎2 𝑏 + 3𝑎𝑏 2 ± 𝑏 3
(𝑥 + 𝑎)(𝑥 + 𝑏) = 𝑥 2 + 𝑥(𝑎 + 𝑏) + 𝑎𝑏
Ejemplos.(4) (x + 4)(x + 3) = x2 + 7x + 12.
(5) (m + 5)(m – 3) = m2 + 2m – 15 .
(6) (3x – 2)(3x – 8) = 9x2 – 30x + 16.
Ejercicios: Desarrolla por simple inspección.
Ejemplos.(7) (𝑝 + 2)3 = 𝑝3 + 3 ∙ 𝑝2 ∙ 2 + 3 ∙ 𝑝 ∙ 22 + 23
= 𝑝3 + 6𝑝2 + 12𝑝 + 8
(8)
(2𝑡 − 𝑟)3 = (2𝑡)3 − 3(2𝑡)2 ∙ 𝑟 + 3(2𝑡) ∙ 𝑟 2 − 𝑟 3
= 8𝑡 3 − 3 ∙ 4𝑡 2 ∙ 𝑟 + 6𝑡 ∙ 𝑟 2 − 𝑟 3
= 8𝑡 3 − 12𝑡 2 𝑟 + 6𝑡𝑟 2 − 𝑟 3
Ejercicios Desarrolla por simple inspección los siguientes cubos de Binomio.