BALOTARIO CUARTOOOOOOOOOOOOOO

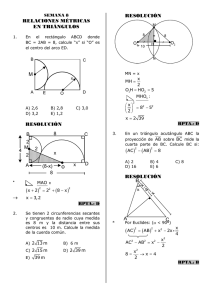
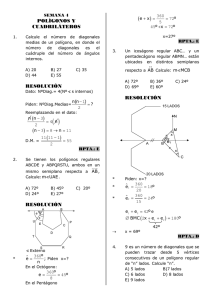
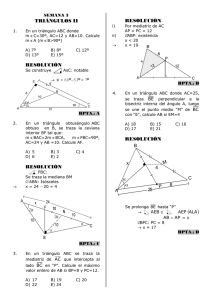
. Calcula la medida de , si AB = DC:
Si: AC=16. Hallar el perímetro del triángulo ABE
Hallar “x” si BP = BA; BQ = BC
Las bases de un trapecio rectángulo miden 28 y 18cm. Si un lado no paralelo forma 45 0 con la
base, ¿Cuál es el área del trapecio?
1. Hallar AB, si CD =6 y AC = 14
B
. En la fig. se cumple que: 3 + 2x = 18. Hallar
1.
2.
3.
4.
5.
1.
6.
E=
+x
Si las diagonales de un rombo miden 12 y 12
cm . ¿Cuánto mide el lado del rombo?
a)10
b)12
c)15
d)N.A
El área de un cuadrado es 72cm2. Calcula la distancia del centro del cuadrado a un lado.
a)3
b) )2
c) )
d)N.A
El perímetro de un rombo mide 80cm. Si la diagonal menor mide 24cm. Halla su área.
a)389cm2
b)384cm2
c)358cm2
d)N.A
Las bases de un trapecio rectángulo miden 28 y 18 cm . Si un lado no paralelo forma 45 0 con la base.
¿Cuál es el área del trapecio?
a)245cm
b)230cm2
c)278cm2 d)N.A
La base mayor de un trapecio mide 22cm. Si la mediana mide 18cm, halla su base menor.
ABCD es un trapecio isósceles. Halla su área.
a)72
b) 96
c) 68
d)N.A
Encontrar la relación de las bases de un trapecio, la relación de la mediana y del segmento que une los
puntos medios de las diagonales es de 3 a 2.
a)5
b)7

c)9
d)11

01. En la siguiente figura, si L 1// L 2 . Calcule el suplemento de “x”
L1


xº
50º
L2
Rpta: 65


02. En la siguiente figura, si L 1// L 2 . Calcule el valor de “x”
x
L1
L2
2

50º
Rpta: 105º


03. En la siguiente figura, si L 1// L 2 . Calcule el complemento de “x”
L1
100º
L2
120º
Rpta: 50º
x
 
04. En la siguiente figura, si L1// L 2 . Calcule el valor de “x”
x
150º
L1
60º
L2


Rpta: 30º

05. En la siguiente figura, si: AB// DE// CF . Calcule el suplemento de “x”
A
B
50+
Rpta: 30º
D
E
x
+
20
F
C


06. En la siguiente figura, si L 1// L 2 . Calcule el valor de “x”
L1
85º
25º
x
Rpta: 120º
L2
 
07. En la siguiente figura, si L1// L 2 . Calcule el valor de “x”
140º
L1
xº
L2
150º
Rpta: 70º


08. En la siguiente figura, si L 1// L 2 . Calcule el complemento de “”
L1
30º
70º
100º

L2
Rpta: 30º


09. En la siguiente figura, si r // s . Calcule el suplemento de “x”


40º
r
xº


s