GEOMETRIA 3º semana CS

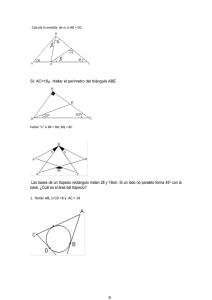
SEMANA 3
RESOLUCIÓN
TRIÁNGULOS II
i)
1.
En un triángulo ABC donde
m ∢ C=30º, AC=12 y AB=10. Calcule
m ∢ A (m ∢ B>90º)
B) 8º
E) 15º
→
C) 12º
x
A) 7º
D) 13º
ii)
Por mediatriz de AC
AP = PC = 12
∆ABP: existencia
x < 20
x = 19
RESOLUCIÓN
Se construye
AsC: notable
→ x = 60º−53º = 7º
S
RPTA.: B
6 3
B
6
4.
10
A
53º
x
30
C
12
RPTA.: A
2.
En un triángulo obtusángulo ABC
obtuso en B, se traza la ceviana
interior BF tal que:
m ∢ FBC=90º,
m ∢ BAC=2m ∢ BCA,
AC=24 y AB =10. Calcule AF.
A) 5
D) 6
B) 3
E) 2
A) 18
D) 17
B
4
α
α
A
2α
α
En un triángulo ABC se traza la
mediatriz de AC que intercepta al
lado BC en “P”. Calcule el máximo
valor entero de AB si BP=8 y PC=12.
B) 19
E) 24
C
25
P
8
Se prolonga BE hasta “P”
→
AEB ≅
AEP (ALA )
AB = AP = x
∆BPC: PC = 8
→ x = 17
RPTA.: D
RPTA.: C
A) 17
D) 22
M
x
α
3.
C) 16
C) 4
FBC:
Se traza la mediana BM
∆ ABN: Isósceles
x = 24 − 20 = 4
2α
B) 15
E) 21
RESOLUCIÓN
RESOLUCIÓN
→
En un triángulo ABC donde AC=25,
se traza BE perpendicular a la
bisectriz interna del ángulo A, luego
se une el punto medio “M” de BC
con “E”, calcule AB si EM=4
C) 20
5.
RESOLUCIÓN
B
Calcule “x” en la figura si:
AB = BE y BC =BD
B
A) 30º
22º
45º
C
x
x
x
C) 50º
D) 53º
45º
A
A
D
3x
E) 20º
B
C
x
Se traza la mediana BM y la altura
BH
BHM: notable (45º)
→
2x =
→
θ
x=
θ
C
10
20
E
x α
22º 30
M
H
10
RESOLUCIÓN
A
10
2x
B) 45º
D
3x
10
2
10
2
2 2
2
=
5 2
2
RPTA.: D
E
i)
ii)
∆ ABD ≅ ∆ EBC .......(L.A.L.)
m ∢ BAD = m ∢ BEC = θ
Por propiedad:
7.
En
un
triángulo
ABC
donde
m ∢ B=150º, m ∢ c =10º y la
distancia de “C” a la bisectriz del
ángulo “A” es 4. Calcule AB.
x − θ = θ + 180º−3x
4x = 180º
x=45º
RPTA.: B
6.
En un triángulo rectángulo ABC
donde mB= 90º, mC = 22º 30’,
AC=20. Calcule la distancia del punto
medio de BC a la hipotenusa.
10 2
3
5 2
D)
2
A)
5 2
3
5 2
E)
4
B)
C) 5 2
A) 4
B) 6
D) 10
E) 2
C) 8
RESOLUCIÓN
A
x
2
10º
60º 1x
0º
C
10º
150º
30º
4
B
H
T
Se traza la altura AT
ATC ≅
AHC (ALA)
AT = CH
x
=4→x=8
2
RPTA.: C
8.
En un triángulo ABC donde m ∢ A
= 48º,
se
traza
la ceviana
interior BM tal que: m ∢ ABM =18º y
AB = MC. Calcule m ∢ C.
A) 18º
D) 48º
B) 28º
E) 66º
C) 37º
En la figura: ABCD es un cuadrado, las
distancias de “B” y “C” a AF son “b” y “c”
respectivamente. Calcule la distancia de
“D” a AF .
RESOLUCIÓN
Se traza BP = BM
∆ ABP ≅ ∆ BMC (L.A.L.)
→
∧
∧
m A =m C =48º
b+c
4
b
D)
2
A)
B)
b−c
2
C) b − c
E) c
RESOLUCIÓN
Triángulos rectángulo congruentes.
x=b−c
B
C
x
c
c
b
RPTA.: D
9.
En un triángulo rectángulo ABC recto
en B, “F” es el excentro relativo al
lado AC. Calcule FB si la distancia de
“F” a AC es 6.
x
θ
A
θ
α
D
RPTA.: C
A) 3 2
B) 9
D) 6 2
E) 8
C) 12
10.
RESOLUCIÓN
El excentro edidista de los lados
→
BPF
x=6 2
B
45º 45º
Q
A α
α
x
6
C
6
F
RPTA.: D
Se tiene el cuadrilátero
ABCD
donde AB=BC, BD=AC y m ∢ CAD =
90º. Calcule m ∢ BDA.
A) 37º
D) 53º
B) 45º
E) 30º
C)60º
12.
Calcule “x” en la figura.
RESOLUCIÓN
Se construye ∆PCD
i)
BH
→
PD
2BHD = AC = 2a
BHD : notable
→
x = 30º
A) 30º
D) 40º
C
α
B) 32º
E) 45º
C) 35º
RESOLUCIÓN
2a
B
B
a
θ
θ
P
2a
α
8
D
x
A
RPTA.: E
En el triángulo rectángulo ABC
(m ∢ B=90º) donde AB=BC, se ubica
el
punto
interno
“P”
siendo:
m ∢ PAB=m ∢ PCA y AB=AP. Calcule:
m ∢ PAC
A) 10º
D) 20º
8
x
A
H
11.
C
x
B) 15º
E) 24º
C) 18º
i)
→
ii)
75º
16
Se traza CH AD
CH = 8
∆ACD: Propiedad
x = 30º
13.
RPTA.: A
Calcule “x”. Si: AB=DC
RESOLUCIÓN
B
a 2
H
45
A) 40º
D) 30º
P
x
α
a
B) 35º
E) 25º
C) 32º
RESOLUCIÓN
B
C
40º x
2a
P
A
AHC notable (30º, 60º)
α = 30º
∆APC: x + 30º =45º
x = 15º
x
x
A
40+x
x
x
C
D
RPTA.: B
i)
ii)
→
→
Se traza bisectriz: AP
Se traza PD → ∆ABPD: Inscriptible
∆ABP ≅ ∆PDC...............(L.A.L.)
∆ABP:
4x + 40º = 180º
4x = 140
x = 35º
RPTA.: B
En el triángulo rectángulo ABC
( m∢B = 90º ) donde AB = BC, se
RESOLUCIÓN
B
considera interiormente el punto
“P” siendo AP = BC y m ∢ PAC
=15º. Calcule m ∢ PCA
A) 20º
D) 35º
B) 25º
E) 40º
α α
x
13
x
C) 30º
E
A
3
P
14.
F
C
RESOLUCIÓN
0
i)
Se traza OP
BC
ii)
iii)
i)
→
Se construye ∆AEC: equilátero
∆ ABE ≅ ∆ BEC ≅ ∆PAC (L.A.L.)
∴ x= 30º
RPTA.: C
15.
En la figura, calcule “BC” si: AB
=13, AE = 3 y AF = FC.
A) 16
B) 17
α α
Por Bisectriz: OE = OP
→
EB = BP = 16
Por mediatriz: OA = OC
AEO ≅
OPC
→
EA=PC=3
∴ x = 16 + 3 = 19
RPTA.: D
16.
En el triángulo ABC se traza la
ceviana BQ que intercepta a la
mediana AP en su punto medio “N” ,
luego se ubica el punto medio “E” de
BP tal que AE intercepta a BQ en
el punto M. Calcule: MN si BQ= 24
A) 6
D) 8
B) 3
E) 5
C) 18
RESOLUCIÓN
D) 19
E) 20
C) 2
i)
→
∴
Se traza PF//BQ
∆PAF
PF = 2NQ = 2b
∆BQC
BQ = 2PF = 4b
∆ABP: “M”: Baricentro
MB = 2MN = 2x
b=x
24
=6
x=
4
i)
Se traza la altura BH
ii)
iii)
Se construye
AED(notable)
Propiedad bisectriz
AE = AH = a
∆DAC: Isósceles: 2x = 100º
x = 50º
iv)
RPTA.: D
18.
Calcule “α” en la figura:
Si: AD = BC
RPTA.: A
17.
En la figura: AB = BC, m ∢ ABC
= 40º, m ∢ DBA = 20º y m ∢ DAB =
10º. Calcule: m ACD.
α
6α
2α
A) 10º
D) 18º
B) 12º
E) 20º
C) 15º
RESOLUCIÓN
B
A) 40º
D) 50º
B) 45º
E) 54º
5α α α
C) 48º
5α
α
RESOLUCIÓN
B
α
A
i)
20 20
ii)
20
D
→
x
2a
10
a
60º 70º
A
a
2α
α
α
α
D
C
Se construye
∆APD ≅ ∆BDC....(L.A.L.)
∆ ABD (Isósceles)
3α+3α+6α=180º
12α=180º
α =15º
RPTA.: C
30º
E
P
x
H
a
C
19.
En la figura AB = PC, BF = FC, AE
= EP. Calcule “x”.
A) 18º
D) 22º
B) 19º
E) 24º
C) 20º
RESOLUCIÓN
i)
Propiedad mediatriz: BQ = QC y AQ
= QP
∆ ABQ ≅ ∆ PQC (L.L.L.)
m QCP =m ABQ=2x
ABC:5x = 90º
90
x=
= 18º
5
RPTA.: A