ENSAYO SOBRE TEORIA DE CONTROL 1

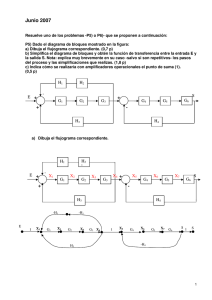
ENSAYO SOBRE TEORIA DE CONTROL 1
Antes de analizar los sistemas de control, deben definirse ciertos términos básicos como son los
siguientes:
Sistema: es un conjunto de componentes que actúan entre sí para un fin determinado. Un
sistema no necesariamente es físico sino que también puede ser abstracto como por ejemplo un
sistema económico. Existen sistemas físicos, químicos, políticos, sociales, electrónicos,
neumáticos, etc.
Control realimentado: es aquella operación, en presencia de perturbaciones, en la que se
puede reducir la diferencia entre la salida de un sistema y alguna entrada de referencia y lo
continua haciendo en base a esa entrada de referencia.
Sistema de control automático: es aquel en el que no existe intervención humana.
Los sistemas de control se pueden dividir en sistemas de lazo abierto y lazo cerrado.
En los sistemas de lazo abierto la salida no afecta la acción de control o mejor dicho, no existe
algún dispositivo de realimentación que compare la salida con la entrada y haga ajustes al
respecto. El ejemplo más usual de un sistema de lazo abierto es el de una lavadora, en la cual el
lavado y enjuague operan con una base de tiempo. La maquina no mide la señal de salida, que
es la limpieza de la ropa.
Los sistemas de control de lazo cerrado son los llamados retroalimentados. En un sistema de
control en lazo cerrado, se alimenta al controlador la señal de error de actuación, que es la
diferencia entre la señal de entrada y la señal de realimentación con el fin de reducir el error y
obtener una salida conveniente. Un ejemplo de sistema de control en lazo cerrado son los
servofrenos de algunos vehículos, los cuales varían la intensidad del frenado conforme se
requiera.
Para representar los sistemas de control se utilizan varias nomenclaturas entre ellas los
diagramas de bloques. Estos diagramas representan partes de un proceso de control las cuales
se muestran a continuación.
Figura 1
Cuando H(s) es igual a 1 quiere decir que se trata de un elemento simple casi sin perdidas de
señal (pista, tubo, alambre, cable, etc.).
La función de transferencia de un circuito es la relación que existe entre la señal de salida y la de
entrada. Esta relación, en los sistemas en lazo cerrado, se describe con la siguiente formula:
C ( s)
G( s)

R( s) 1  G ( s) H ( s)
En donde 1  G( s) H ( s) es llamada la ecuación característica.
En la función de transferencia en lazo abierto la ecuación quede como sigue:
B( s)
 G( s) H ( s)
E ( s)
Para resolver cualquier sistema representado en diagrama de bloques que sea relativamente
complejo se pueden emplear algunas técnicas las cuales consisten en:
1.- Álgebra de diagramas de bloques.
2.- Flujogramas.
3.-Algoritmo de Mason.
Cualquier técnica de reducción esta encaminada a encontrar la función de transferencia total del
sistema o lo que es la salida entre la entrada (
C (s)
) , que no es otra cosa mas que la ganancia.
R(s)
En el álgebra de diagramas de bloques lo que se busca es reducir hasta la mínima expresión del
control los bloques como se muestra en la figura 1 exceptuando el selector de referencia..
En el caso de tener varias entradas, se anulan todas menos una, con la cual se reduce todo el
complejo de bloques y se obtiene una salida parcial. Cuando se tienen todas las salidas parciales
se suman algebraicamente para obtener la salida total.
La reducción de los bloques para obtener las salidas parciales se realiza con unas tablas de
reducción las cuales nos indican las equivalencias que hay entre diversos acomodos de ramas
(flechitas) y bloques (recuadros) con el fin de acercarnos lo más posible a la mínima expresión
del control.
Un flujograma es un diagrama que puede suplir a los diagramas de bloques bajo las mismas
reglas de reducción y además serán de utilidad cuando los sistemas se presenten medianamente
complejos.
Para pasar un sistema en bloques a un flujograma, se cambian los recuadros por flechas
llamadas ramas y los puntos de suma por nodos como se muestra en la figura 2.
Figura 2
El algoritmo de Mason se realiza solo con flujogramas y consiste en aplicar una sencilla formula
que aparece a continuación.
 Pkk
En donde G es la ganancia, Pk son el numero de trayectorias directas desde la

entrada principal hasta la salida,  k es el cofactor del determinante que regularmente tiene valor
de 1 y  es el numero de todos los lazos cerrados que hay.
G
Teoría de control 2
Valdovinos Villalobos Gerardo