Calcular las dimensiones del triángulo isósceles de mayor área

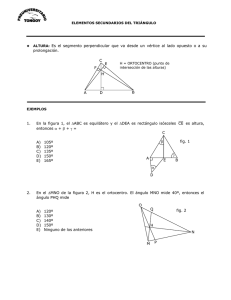
Calcula las dimensiones del triángulo isósceles de mayor
área inscrito en una circunferencia de radio R.
SOLUCIÓN:
Las variables que vamos a utilizar serán b, base y h, altura
del triángulo.
La función a maximizar es su área, es decir: A =
bh
.
2
Para ponerlo en función de una sola variable buscamos
una relación entre b, h y los datos, en este caso R. En el triángulo pequeño:
2
(h -
R)2
 b
+   = R2
 2
h2 - 2hR + R2 +
8Rh  4h 
A=
b2
= R2, con lo que: b2 = 8Rh - 4h2 y sustituyendo en A:
4
2 1/ 2
h
2
8Rh

3
 4h4

1/ 2
2
, donde hemos introducido h dentro de la raíz cuadrada
(exponente 1/2) multiplicando el radicando por h2.
El área ya está ahora en función de una variable.
Se trata de maximizar la función, para lo que buscaremos entre los ceros de la derivada
(pendiente horizontal) el valor que la haga máxima:
A’ =
24Rh2  16h3
4 8Rh3  4h4

2h2 3R  2h
8Rh3  4h4
, A’ = 0 si h = 0, que no soluciona el problema, y si h =
3R
.
2
Para ver si en este valor se obtiene un máximo, analizamos el crecimiento a su izquierda y su
derecha con el signo de la derivada.
Como el signo de A’ depende sólo de 3R - 2h, obtendremos:
A’ > 0, si h <
3R
, y A creciente;
2
A’ < 0, si h >
3R
3R
, y A decreciente; por lo que en
la función pasa de creciente a decreciente
2
2
con lo que se obtendrá un valor máximo para ese valor de h.
Para h =
3R
se obtiene b =
2
3R, que serán las dimensiones del triángulo isósceles pedido.