solucion EX SEPT11

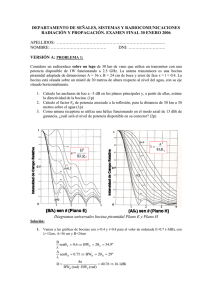
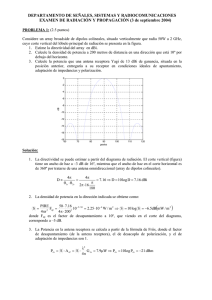
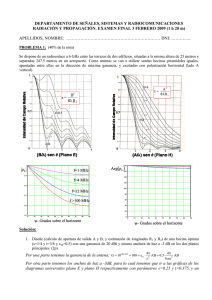
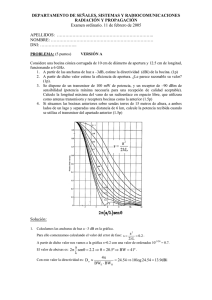
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN
Examen extraordinario. 12 de septiembre de 2011
APELLIDOS: …………………………………………………………..
NOMBRE: ………………………………………………………………
DNI: ……………………..
PROBLEMA 1: (3 puntos)
Considere un radioenlace de corta distancia a
10 GHz través de un lago. Las antenas son dos
bocinas cónicas corrugadas de 10 cm de
diámetro con polarización vertical y error de
fase s=0.2 y están situadas a 612.5 cm del
suelo.
1. Estime la directividad de las bocinas.
(1.5p)
2. Calcule las pérdidas del radioenlace
considerando el lago, con coeficiente
de reflexión de -1, si la separación
entre antenas es de 1000 metros.
(1.5p)
Diagrama universal de la bocina cónica
corrugada
Solución:
1. El radio de la bocina es a=5 cm y la longitud de onda es λ=30/10GHz=3 cm.
Para calcular el ancho de haz a -3dB, vamos a la gráfica al corte de 0.707 con s=0.2 y
obtenemos en abcisas:
a
2 sin   2.2    12.12º  BW3dB  2  24.25º

La directividad se obtiene a partir del ancho de haz a -3dB:
41253
D  10 log
 18.5dBi
BW 2
2. Para calcular las pérdidas del radioenlace:
Lradioenlace  Lel  Gtx  Grx  Lreflexion
Las ganancias de las antenas son equivalentes a la directividad.
4d
Las pérdidas de espacio libre son: Lel  20 log
 112.4dB

Las pérdidas por reflexión se calculan a partir de la suma del rayo directo y reflejado:
2



 

 j R 
Etot  Ed  Er  Ed  1    e    2  Ed  Lreflexion  20 log 2  6dB


R  1000 2  4h 2  1000  7.5cm
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN
Examen extraordinario. 12 de septiembre de 2011
APELLIDOS: …………………………………………………………..
NOMBRE: ………………………………………………………………
DNI: ……………………..
PROBLEMA 2: (3 puntos)
Considere el dipolo de la figura enfrentado y paralelo al plano conductor que puede
suponerse indefinido, funcionando a 1.5 GHz.
L=9.3 cm
5 cm
Soporte
Plano Reflector
Línea
Coaxial
Zc =50 
kL/2
Impedancia mutua entre dos dipolos
idénticos, paralelos, enfrentados y
separados /2
1. Si la autoimpedancia del dipolo aislado es de 70-j24 , calcule la impedancia de
entrada del dipolo enfrentado al plano (impedancia vista por el cable coaxial de 50 ohm en
su extremo superior) aplicando imágenes. (1.5p)
2. Calcule las pérdidas por desadaptación de impedancia cuando se alimenta con un
transmisor adaptado a la línea coaxial de 50  que lo excita. (1.5p)
Solución:
1. La impedancia de entrada se calcula aplicando el teorema de las imágenes. El dipolo sobre
el plano de masa se puede sustituir por dos dipolos separados 10 cm y excitados con
corrientes opuestas. En este caso:
V
V1  I1 z11  I 2 z12  I1 z11  I1 z12  Z in  1  70  j 24   10  j 24   80
I1
donde z11 está en el enunciado y z12 se obtiene de la gráfica para:
kL 2L

 1.46  z12  10  24 j
2
2


2. Las pérdidas por reflexión se calculan como: Lrefl  10 log 1   2  0.24dB , donde el
coeficiente de reflexión es:

Z in  Z o
 0.23
Z in  Z o
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
EXAMEN DE RADIACIÓN Y PROPAGACIÓN
Examen extraordinario. 12 de septiembre de 2011
APELLIDOS: …………………………………………………………..
NOMBRE: ………………………………………………………………
DNI: ……………………..
TEORÍA (4 puntos)
1. ¿Qué tipo de antenas se utilizan típicamente como transmisoras de radiodifusión en
onda media? Diga en qué orden de tamaños reales se encuentran y algunas de sus
características eléctricas (diagrama de radiación, polarización, ganancia...) (0.5p)
Las antenas que se utilizan son los mástiles o torres, que consisten en monopolos sobre
plano de masa. Los monopolos tienen unas dimensiones de cuarto de longitud de onda,
que a la frecuencia de 1 MHz, son 75 metros. El diagrama de radiación es
omnidireccional, la polarización vertical (única posible en onda de superficie) y las
ganancias pequeñas: la directividad del monopolo λ/4 es de 5.15 dBi.
2. Cite las principales características de las antenas Yagi. ¿Qué ganancias pueden
conseguir? ¿Qué aplicaciones tienen? ¿En qué bandas de frecuencias se utilizan
habitualmente? (0.5p)
Las Yagis son arrays de dipolos paralelos en las que sólo se alimenta de forma
directa el excitador, haciéndolo los demás (reflector/s y directores) por
acoplamiento mutuo. Las ganancias son desde unos 7dBi para 2 elementos a
17/18 dBi para unos 30 directores. La aplicación fundamental es como antena
receptora de señales de TV en las bandas de VHF (60-300MHz) y UHF
(300MHz hasta unos 850MHz).
3. Un array endfire de cinco dipolos trabajando a 1 GHz, tiene una separación entre
elementos de 40 cm y una ganancia de 50 dBi. Comente las incongruencias de esta
frase. (0.5p)
A 1 GHz la longitud de onda son 30 cm, con lo que no puede haber una separación
entre elementos de 40 cm (la separación debe ser menor de λ/2 para que no existan
lóbulos de difracción en los arrays endfire). Tampoco puede haber una ganancia de 50
dBi con arrays de estas dimensiones a esta frecuencia.
4. Una antena transmisora radia polarización elíptica a izquierdas de 20 dB de relación
axial y eje mayor según el eje x. Razone con cuál de estas polarizaciones de antena
receptora se recibirá la máxima potencia: circular a izquierdas, circular a derechas,
lineal sobre x o lineal sobre y. (0.5p)
Una relación axial de 20 dB da una polarización prácticamente lineal. Como la elipse
está con el eje mayor según el eje x, será con una polarización lineal según el eje x con
lo que se reciba la máxima potencia.
5. Un radioenlace a 30 GHz de 20 km de distancia se ve afectado por una lluvia de
25litros/hora. Comente los efectos sobre el mismo. (0.5p)
A 30 GHz el efecto de la lluvia es apreciable: provoca atenuación de la señal,
despolarización de la señal, aumento del nivel de ruido.
6. Una bocina piramidal óptima tiene una directividad de 18 dBi a 500 MHz. Estime las
dimensiones de la antena. (0.5p)
La bocina piramidal óptima tiene una eficiencia de apertura de 0.5. Por lo tanto
podemos
extraer
el
área
de
la
apertura
como:
D  a 
4

2
Sa   a 
4

2
A  B  1018 /10  A  B  36151cm 2
Haciendo A≈1.4B para que los anchos de haz sean similares, obtenemos: B=160,7cm y
A=225cm
7. Un reflector Cassegrain centrado, de 1.5 metros de diámetro posee una ganancia de 46
dBi a 15 GHz, cuando se ilumina con una bocina cónica corrugada de 20 dBi de
ganancia. Si se cambia la bocina de alimentación por otra de 15 dBi de ganancia, diga
cómo varían los distintos parámetros (ganancia, ancho de haz, lóbulos, eficiencias ...) de
la antena reflectora. (0.5p)
Para empezar comprobamos en qué punto se encuentra: para ello calculamos la
eficiencia de apertura del reflector:
2
4
4   
G  D   a  2 S a   a  2     10 46 /10   a  0.72 , que es un valor que

 2
corresponde al óptimo. Por lo tanto, cualquier cambio de configuración hará que la
ganancia y directividad se reduzcan. Al pasar a una bocina de menor ganancia, el
reflector se iluminará de manera más uniforme con lo que la eficiencia de iluminación
aumentará, el haz principal se estrechará y aumentarán los lóbulos secundarios. Por el
contrario la eficiencia de spillover se reducirá, y también la eficiencia total (al ir a una
situación no óptima).
8. Una antena que posee una impedancia de entrada de 75+j10 y un rendimiento de
radiación de 0.85 se alimenta a través de un cable coaxial sin pérdidas de 50,
conectado a un generador de 50 con una potencia disponible de 2W. Calcule la
potencia radiada por la antena. (0.5p)
La potencia radiada se calcula a partir del rendimiento de radiación y las pérdidas por
desadaptación de impedancias como:
 75  j10  50 2 
2
Prad   rad  Pent   rad  1  tx  Pdis  0.85  1 
  2W  1.62W
 75  j10  50 

