ex feb06

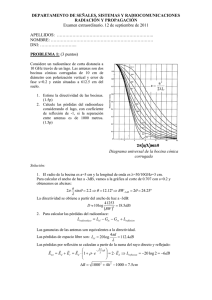
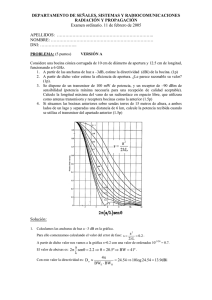
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 30 ENERO 2006
APELLIDOS: ………………………………………………………….............
NOMBRE: …………………………………
DNI: ……………………..
VERSIÓN A: PROBLEMA 1:
Considere un radioenlace sobre un lago de 30 km de vano que utiliza un transmisor con una
potencia disponible de 1W funcionando a 2.5 GHz. La antena transmisora es una bocina
piramidal adaptada de dimensiones A = 36 x B = 24 cm de boca y error de fase s = t = 0.4. La
bocina está situada sobre un mástil de 30 metros de altura respecto al nivel del agua, con su eje
situado horizontalmente.
1. Calcule las anchuras de haz a –3 dB en los planos principales y, a partir de ellas, estime
la directividad de la bocina. (1p)
2. Calcule el factor Fp de potencia asociado a la reflexión, para la distancia de 30 km a 30
metros sobre el agua (1p)
3. Como antena receptora se utiliza una hélice funcionando en el modo axial de 13 dBi de
ganancia, ¿cuál será el nivel de potencia disponible en su conector? (2p)
Diagramas universales bocina piramidal Plano E y Plano H
Solución:
1.
Vamos a las gráficas de bocinas con s=0.4 y t=0.4 para el valor de ordenada E=0.7 (-3dB), con
λ=12cm, A=36 cm y B=24cm
B
senθ E = 0.6 ⇒ BWE = 2θ E = 34.9º
λ
A
senθ H = 0.75 ⇒ BWH = 2θ H = 29º
λ
4π
D=
= 40.76 ⇒ 16.1dBi
BWH (rad) ⋅ BWE ( rad)
2. Para el cálculo del factor de potencia, consideramos la suma vectorial del rayo directo y el rayo
reflejado.
(
)
r
r
r
r
r
E t = E d + E r = E d ⋅ 1 + ρ ⋅ e − jk o ∆d = 2 ⋅ E d ⇒ Fp = 20 log 2 = 6dB
donde:
ρ= -1 (reflexión en el agua)
∆d=0.06 metros (diferencia de caminos entre rayo reflejado y directo)
λ=0.12m (longitud de onda)
ko=2π/λ
3. Como la hélice en modo axial tiene polarización circular, y las bocinas polarización lineal,
tenemos unas pérdidas por desacoplo de polarización de 3 dB. Aplicando la fórmula de Friis
tenemos:
4πd
+ Fp (dB) + G rx (dBi) − L pol (dB) =
λ
= 30dBm + 16.1dBi − 129.9dBi + 6dB + 13dBi − 3dB = −67.8dBm
Prx (dBm) = Ptx (dBm) + G tx (dBi) − 20 log
DEPARTAMENTO DE SEÑALES, SISTEMAS Y
RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 30 ENERO 2006
APELLIDOS: ………………………………………………………….............
NOMBRE: …………………………………
DNI: ……………………..
VERSIÓN A: PROBLEMA 2:
Considere el dipolo de la figura enfrentado y paralelo al plano conductor que puede suponerse
indefinido, funcionando a 1 GHz.
L=14 cm
Soporte
7.5 cm
Plano Reflector
Línea
Coaxial
Zc =50Ω
kL/2
Impedancia mutua entre dos dipolos
idénticos, paralelos, enfrentados y
separados λ/2
1. Si la autoimpedancia del dipolo aislado es de 68-j24 Ω, calcule la impedancia de
entrada del dipolo enfrentado al plano (impedancia vista por el cable coaxial de 50 ohm en
su extremo superior) aplicando imágenes. (1p)
2. Calcule las pérdidas por desadaptación de impedancia cuando se alimenta con un
transmisor adaptado a la línea coaxial de 50 Ω que lo excita. (1p)
Solución:
1. Vamos a la gráfica de impedancias mutuas de dos dipolos con un valor de abcisas: kL/2 = 1.47,
donde:
k=2π/λ; λ=30 cm; L=14 cm
En la gráfica obtenemos: z12=-10-j24 Ω. El valor de la impedancia de entrada es entonces: Zin=
z11 – z12 = 78 Ω
2. Para el cálculo de las pérdidas por desadaptación, calculamos el coeficiente de reflexión a la
línea (Zo=50Ω):
Γ=
(
)
Z in − Z o
2
= 0.22 ⇒ L des = −10 log 1 − Γ = 0.43dB
Z in + Z o
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 30 ENERO 2006
APELLIDOS: ………………………………………………………….............
NOMBRE: …………………………………
DNI: ……………………..
VERSIÓN A: TEORÍA:
1. Una antena posee una impedancia de entrada de 75+j10Ω y un rendimiento de radiación
de 0.9. Sabiendo que cuando se alimenta con una corriente de 2A de pico genera a 1 km
de distancia en la dirección de máxima radiación una densidad de potencia de 1
mW/m2, calcule la ganancia de la antena en dBi. (1p)
S =
donde: Ptx =
4πr 2 S
PIRE Ptx ⋅ g t
⇒
g
=
= 83.8 ⇒ 10 log 83.8 = 19.2dBi
=
t
Ptx
4πr 2
4πr 2
1 2
I R in = 150 W
2
2. Una antena con un haz tipo pincel tiene una ganancia de 11 dBi. Sabiendo que el campo
eléctrico en el lóbulo principal varía como cos4θ, calcule la ganancia de potencia en dBi
para la dirección θ=20º y φ=30º. (1p)
L des = 20 log cos 4 20º = −2.16dB ⇒ G (θ = 20º ) = 11dBi − 2.16dB = 8.84dB
3. Un reflector Cassegrain centrado, de 1.5 metros de diámetro posee una ganancia de 46
dBi a 15 GHz, cuando se ilumina con una bocina cónica corrugada de 20 dBi de
ganancia. Si se cambia la bocina de alimentación por otra de 15 dBi de ganancia, diga
cómo varían los distintos parámetros (ganancia, ancho de haz, lóbulos, eficiencias ...) de
la antena reflectora. (1p)
Comenzamos calculando la eficiencia total: G =
4π
ε t A ap = 10 4.6 ⇒ ε t = 0.72
λ2
Por lo tanto, la situación de partida es con antena óptimamente iluminada. Al reducir la ganancia
del alimentador, su haz principal se ensancha, de modo que ilumina la apertura del reflector más
uniformemente (C mayor en el borde). Esto se traduce en un aumento de la eficiencia de
iluminación y decrecimiento de la eficiencia de spillover. La ganancia total y la eficiencia total
disminuyen al pasar de una situación óptima a otra distinta. La forma de iluminación más
uniforme se traduce en una reducción (ligera) de la anchura del lóbulo principal y un aumento de
los lóbulos secundarios.
4. ¿Qué alcance se puede conseguir por propagación ionosférica a 100 MHz? Explique su
respuesta. (1p)
En esta frecuencia, la densidad de electrones de la ionosfera no es capaz de reflejar el rayo hacia
la Tierra, y la onda sale hacia el espacio exterior, con lo que no se puede establecer
comunicaciones por propagación ionosférica a estas frecuencias.
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 30 ENERO 2006
APELLIDOS: ………………………………………………………….............
NOMBRE: …………………………………
DNI: ……………………..
VERSIÓN B: PROBLEMA 1:
Considere un radioenlace sobre un lago de 15 km de vano que utiliza un transmisor con una
potencia disponible de 1W funcionando a 3.75 GHz. La antena transmisora es una bocina
piramidal adaptada de dimensiones A = 24 x B = 20 cm de boca y bajo error de fase. La bocina
está situada sobre un mástil de 30 metros de altura respecto al nivel del agua, con su eje situado
horizontalmente.
1. Calcule las anchuras de haz a –3 dB en los planos principales y, a partir de ellas, estime
la directividad de la bocina. (1p)
2. Calcule el factor Fp de potencia asociado a la reflexión, para la distancia de 15 km a 30
metros sobre el agua (1p)
3. Como antena receptora se utiliza una hélice funcionando en el modo axial de 10 dBi de
ganancia, ¿cuál será el nivel de potencia disponible en su conector? (2p)
Diagramas universales bocina piramidal Plano E y Plano H
Solución:
1.
Vamos a las gráficas de bocinas con s=0 y t=0 para el valor de ordenada E=0.7 (-3dB), con
λ=8cm, A=24 cm y B=20cm
B
senθ E = 0.5 ⇒ BWE = 2θ E = 23.1º
λ
A
senθ H = 0.7 ⇒ BWH = 2θ H = 27 º
λ
4π
D=
= 66.14 ⇒ 18.2dBi
BWH ( rad) ⋅ BWE (rad)
2. Para el cálculo del factor de potencia, consideramos la suma vectorial del rayo directo y el rayo
reflejado.
(
)
r
r
r
r
r
E t = E d + E r = E d ⋅ 1 + ρ ⋅ e − jk o ∆d = 2 ⋅ E d ⇒ Fp = 20 log 2 = 6dB
donde:
ρ= -1 (reflexión en el agua)
∆d=0.12 metros (diferencia de caminos entre rayo reflejado y directo)
λ=0.08m (longitud de onda)
ko=2π/λ
3. Como la hélice en modo axial tiene polarización circular, y las bocinas polarización lineal,
tenemos unas pérdidas por desacoplo de polarización de 3 dB. Aplicando la fórmula de Friis
tenemos:
4πd
+ Fp (dB) + G rx (dBi) − L pol (dB) =
λ
= 30dBm + 18.2dBi − 127.4dBi + 6dB + 10dBi − 3dB = −66.2dBm
Prx (dBm) = Ptx (dBm) + G tx (dBi) − 20 log
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 30 ENERO 2006
APELLIDOS: ………………………………………………………….............
NOMBRE: …………………………………
DNI: ……………………..
VERSIÓN B: PROBLEMA 2:
Considere el dipolo de la figura enfrentado y paralelo al plano conductor que puede suponerse
indefinido, funcionando a 500 MHz.
L=28 cm
Soporte
15 cm
Plano Reflector
Línea
Coaxial
Zc =75Ω
kL/2
Impedancia mutua entre dos dipolos
idénticos, paralelos, enfrentados y
separados λ/2
1. Si la autoimpedancia del dipolo aislado es de 68-j24 Ω, calcule la impedancia de
entrada del dipolo enfrentado al plano (impedancia vista por el cable coaxial de 75 ohm en
su extremo superior) aplicando imágenes. (1p)
2. Calcule las pérdidas por desadaptación de impedancia cuando se alimenta con un
transmisor adaptado a la línea coaxial de 75 Ω que lo excita. (1p)
Solución:
1. Vamos a la gráfica de impedancias mutuas de dos dipolos con un valor de abcisas: kL/2 = 1.47,
donde:
k=2π/λ; λ=60 cm; L=28 cm
En la gráfica obtenemos: z12=-10-j24 Ω. El valor de la impedancia de entrada es entonces: Zin=
z11 – z12 = 78 Ω
2. Para el cálculo de las pérdidas por desadaptación, calculamos el coeficiente de reflexión a la
línea (Zo=75Ω):
Γ=
(
)
Z in − Z o
2
= 0.02 ⇒ L des = −10 log 1 − Γ ≈ 0dB
Z in + Z o
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 30 ENERO 2006
APELLIDOS: ………………………………………………………….............
NOMBRE: …………………………………
DNI: ……………………..
VERSIÓN B: TEORÍA:
1. Una antena alimentada por una corriente de 2A de pico, posee una impedancia de
entrada de 75+j10Ω y un rendimiento de radiación de 0.8. Calcule la densidad de
potencia radiada a 10 km de distancia, para la dirección de máxima radiación, para la
que posee una directividad de 10 dBi. (1p)
PIRE Prad ⋅ d t
=
= 0.96µW / m 2
4πr 2
4πr 2
1
donde: Prad = I 2 R in ⋅ η rad = 120 W
2
S =
2. Un array lineal broadside de elementos isótropos posee una directividad de 10 dBi.
Estime la anchura del haz de radiación entre puntos de potencia mitad en un plano que
contiene el array. (1p)
D=
4π
= 10 ⇒ BW = 0.2rad = 11.5º
2π ⋅ BW
3. Un reflector parabólico simple centrado, de 1.5 metros de diámetro posee una ganancia
de 45.2 dBi a 15 GHz, cuando se ilumina con una bocina cónica corrugada de 11 dBi de
ganancia. Si se cambia la bocina de alimentación por otra de 15 dBi de ganancia, diga
cómo varían los distintos parámetros (ganancia, ancho de haz, lóbulos, eficiencias ...) de
la antena reflectora. (1p)
Comenzamos calculando la eficiencia total: G =
4π
ε t A ap = 10 4.52 ⇒ ε t = 0.6
2
λ
Por lo tanto, la situación de partida es con antena óptimamente iluminada. Al aumentar la
ganancia del alimentador, su haz principal se estrecha, de modo que ilumina la apertura del
reflector menos uniforme (C menor en el borde). Esto se traduce en una disminución de la
eficiencia de iluminación y aumento de la eficiencia de spillover. La ganancia total y la
eficiencia total disminuyen al pasar de una situación óptima a otra distinta. La forma de
iluminación menos uniforme se traduce en un aumento (ligero) de la anchura del lóbulo principal
y una reducción del nivel de los lóbulos secundarios.
4. ¿Qué alcance se puede conseguir por propagación ionosférica a 200 MHz? Explique su
respuesta. (1p)
En esta frecuencia, la densidad de electrones de la ionosfera no es capaz de reflejar el rayo hacia
la Tierra, y la onda sale hacia el espacio exterior, con lo que no se puede establecer
comunicaciones por propagación ionosférica a estas frecuencias.