Índices de volumen y de precios

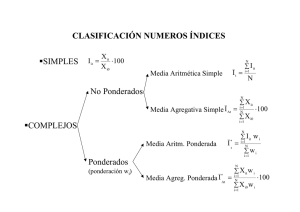
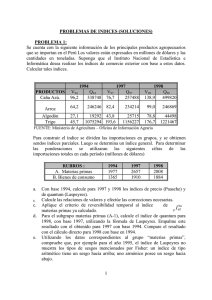
3.4 Índices de volumen y de precios
En este punto, es necesario hacer una relativamente larga
digresión matemática para explicar las nociones de índice de
volumen e índice de precios de manera que el lector pueda
comprender plenamente la manera en que se mide el volumen en
las cuentas nacionales.
Un índice de volumen es una media ponderada de los cambios
entre dos períodos en las cantidades de un determinado
conjunto de bienes o servicios. Tradicionalmente, estos
índices toman un valor de 100 para un período determinado,
aunque en este texto, los índices implícitamente
se
normalizan como 1, y no como 100. Esto es de poca
importancia, sin embargo, debe decirse que los índices de
precios
y
de
volumen
son
números
que
sólo
pueden
interpretarse en términos de evolución. Por convenio, el
período de tiempo utilizado como punto de partida se
denominará como período 0 y el período que se compara con él
como período t. Los dos períodos de tiempo pueden ser
consecutivos o no consecutivos.
Las relaciones de la cantidad o el precio de un producto
determinado en el período t a la cantidad o el precio del
mismo producto en el período 0, es decir, qt/q0 o pt / po, se
conoce como coeficiente de la cantidad y el precio,
respectivamente. Las relaciones de cantidad y de precio son
independientes de las unidades en el que las cantidades y los
precios se miden. La mayoría de los índices se pueden
expresar en la forma de medias ponderadas de los coeficientes
de precio o de cantidad, o se pueden derivar de ellos.
Las
diversas
fórmulas
difieren
principalmente
en
la
ponderación atribuida a las relaciones de cantidad o de
precios y en particular al tipo de media utilizada aritmética, geométrica, armónica, etc.
Los dos índices más comúnmente utilizados son los índices de
Laspeyres
y
Paasche,
llamados
así
en
honor
de
dos
estadísticos del siglo 19. La mayoría de los sistemas de
cuentas nacionales utilizan índices de Laspeyres para el
cálculo de volúmenes e índices de Paasche para calcular las
variaciones en los precios. Tanto los índices de Laspeyres
como de Paasche se pueden definir como medias ponderadas de
los coeficientes de precio o de cantidad, el peso o
ponderación son los valores a precios corrientes de los
bienes o servicios
comparados.
en
uno
u
otro
de
los
dos
períodos
Sea Vij = Pij Qij el valor a precios corrientes del producto i
en el periodo j. El índice de Laspeyres de volumen (LQ) es
una media ponderada de las relaciones de cantidad:
(1)
El periodo que proporciona las ponderaciones del índice se
conoce como el periodo "base". Ello normalmente (pero no
siempre) coincide con el periodo de "referencia" para el cual
el índice tiene un valor estándar de 100. Dado que la suma
siempre involucra el mismo conjunto de bienes y servicios, es
posible prescindir del subíndice i en las expresiones del
tipo (1). Y puesto que Vj, por definición, es igual a PjQj,
también es posible sustituirlo en (1) para obtener (2):
(2)
Algebraicamente, las expresiones (1) y (2) son idénticos.
Esto significa que el cambio en el volumen a precios
constantes se puede calcular de dos maneras con el mismo
resultado: o bien como la media de los cambios en la cantidad
de los diferentes productos ponderados por los valores a
precios corrientes en el año base, o bien, como el monto de
las cantidades en el período t, multiplicados por los precios
del año base dividido por el valor a precios corrientes en el
año base.
El índice de precios de Paasche se puede definir en forma
recíproca al índice de Laspeyres, aplicando los valores a
precios corrientes del período t como ponderaciones y usando
una media armónica de la relación de precios y de las
cantidades en lugar de una media aritmética.
El índice de precios de Paasche Pp se define de la siguiente
manera:
(3)
Se verá a partir de esta fórmula, que lo que se tiene es, en
efecto, un índice de precios, ya que los que varían son los
precios mientras que las cantidades se mantienen fijas, en
contraste con el índice de volumen visto anteriormente. La
reciprocidad entre los índices de Laspeyres y Paasche conduce
a numerosas simetrías que pueden ser explotados en los
cálculos.
En particular, el producto de un índice de volumen de
Laspeyres por un índice de precios de Paasche es igual a la
variación del valor, a precios corrientes del correspondiente
grupo de productos entre el período 0 y t, es decir:
(4)
La fórmula (4) es fundamental en las cuentas nacionales. Su
lectura de derecha a izquierda, muestra que la variación de
un agregado a precios corrientes es igual al producto del
índice de volumen por el índice de precios. Expresa
matemáticamente lo que se ha llamado la "primera ecuación
fundamental "en el Capítulo 1. Esta ecuación es explotada
constantemente en las cuentas nacionales. Por ejemplo, se
utiliza para obtener indirectamente el índice de volumen
dividiendo la variación relativa de los valores por el índice
de precios de Paasche, a través de un método discutido
anteriormente y que se conoce como "deflactación":
(5)
Como generalmente es más fácil, y menos costoso, calcular los
índices de precios que los índices de volumen, es práctica
habitual de las estadísticas económicas el cálculo de
volúmenes mediante la deflación.