EVALUACIÓN DE FÍSICA

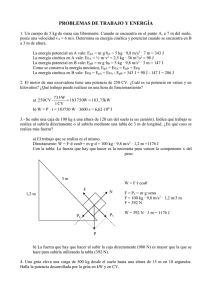
Plan de apoyo cuarto periodo.
Grado 10 ___
NOMBRE: _________________________________________
Las preguntas 1 y 2 se refieren a la siguiente información.
Un cuerpo de masa m posee una energía cinética E cuando su velocidad es v.
1. Para cuadruplicar su energía cinética se debe:
a) Cuadruplicar la velocidad
c) Reducir a la mitad la velocidad.
b) Duplicar la velocidad
d) Reducir a la cuarta parte la velocidad.
2. Para duplicar la velocidad, el trabajo que se debe realizar sobre el cuerpo es:
a) E
b) 2E
c) 4E
d) 3E
3. La energía cinética de un cuerpo se mide en:
a) Vatios
b) Newton
c) Dinas
d) Julios.
4. A un móvil se le aplica una fuerza de 100 Newton. La ecuación que determina su
trabajo es:
a) T = 100 t
b) T = 100 d
c) T = 100 t 2
d) T = 100 d2
5. Después de haberse desplazado una distancia de 120 metros, su trabajo en julios del
móvil anterior será de:
a) 120
b) 1200
c) 12000
d) 120000
6. Si el trabajo del móvil anterior lo realizara en un minuto, su potencia en vatios será:
a) 60
b) 600
c) 12000
d) 200
7. Si lanzamos un cuerpo verticalmente hacia arriba, gana:
a) Gravedad
b) Velocidad
c) Energía cinética
d) Energía potencial
Las preguntas 8 a 16 se basan en el siguiente texto:
Si un cuerpo de masa m se sitúa a una altura h arriba de un nivel de referencia, este
cuerpo posee energía potencial gravitacional con respecto a este nivel, expresada por
Ep=mgh. La energía cinética que tiene un cuerpo es directamente proporcional a la
velocidad al cuadrado:
EC = ½ mV2
Al mismo tiempo, de cinemática, es conocido que la velocidad de un cuerpo que está en
caída libre (desde el reposo) depende de la distancia recorrida y desde el punto de caída:
V2 = 2gy
La energía potencial de un cuerpo depende de la altura y la energía cinética de la
velocidad. Estas dos energías componen la energía mecánica, la cual debe permanecer
constante.
Si un bloque de masa m cae desde un edificio de altura h, según se observa en la figura,
Donde cada punto se ubica exactamente en una posición respecto de la altura h del
edificio: E en 0, D en h/4, C en h/2 es decir en el punto medio del edificio, B en 3h/4 y A
en h es decir en la parte alta del edificio.
8. Podemos expresar la energía cinética del cuerpo que comienza a caer como:
A. EC = mgy = 0
B. EC = mgh = Ep
C. EC = mgy
D. EC = Ep
9. Se puede afirmar que:
La energía potencial del cuerpo a medida que cae y pasa por los diferentes puntos
(indicados como subíndices, es decir EpA quiere decir la energía potencial en el punto A)
es:
A) EpA > EpB>... EpE
C) EpE > EpD> ...EpA
B) EpC > EpB > EpA
D) EpA = EpB =...= EpE
10. La energía cinética del cuerpo al caer y pasa por los diferentes puntos es:
A) ECA> ECB > …>ECE
C) ECE > ECD > …> ECA
B) ECC > ECB > ECA
D) ECA = ECB =... =ECE
11. La energía mecánica (Em) total del cuerpo es
A) EmA > EmB > …>EmE
C) EmE > EmD > …> EmA
B) EmC > EmB > EmA
D) EmA= EmB =... =EmE
12. La energía mecánica total en el punto especificado se puede estimar con las energías
cinéticas y/o potencial excepto en:
A) EmC = EpC + ECA
C) EmB = EpB + ECB
B) EmA = EpA
D) EmE = ECE
13. A medida que el cuerpo cae desde un punto a otro cualquiera, la
A) Ep disminuye y EC aumenta en la misma magnitud manteniéndose la Em constante.
B) Ep aumenta y EC disminuye en la misma magnitud manteniéndose la Em constante.
C) Ep no varía y tampoco EC manteniéndose la Em constante.
D) Ep disminuye y EC permanece constante.
14. Las energías potencial y cinética son máximas y de la misma magnitud
respectivamente en los puntos:
A) A y E
B) E y A
C) C y C
D) B y D
15. Las energías potencial y cinética tienen una magnitud de cero respectivamente en los
puntos:
A) A y E
B) E y A
C) C y C
D) B y D
16. Las energías potencial y cinética tienen la misma magnitud respectivamente en los
puntos:
A) A y E
B) E y A
C) C y C
D) B y D