taller potenciacion y radicacion

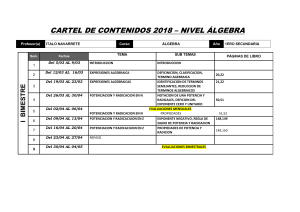
FACULTAD DE INGENIERIA Y CIENCIAS BASICAS
LOGICA Y PENSAMIENTO MATEMATICO – TALLER DE POTENCIACION Y RADICACION
DOCENTE: IDALY MONTOYA A.
ALUMNO: _____________________________________________ PROGRAMA: ____________________
GRUPO: ________ JORNADA: _______ FECHA: ____________ CALIFICACION: _________________
REGLAS
POTENCIACION
a ⋅ a =a
m
n
(a )
m n
RADICAC ION
m+n
1
n
a =n a
m
n
= am ⋅ n
a = n am
(a ⋅ b )n = a n ⋅ b n
a
m
n
=
( a)
m
n
n
an
a
  = n
b
b
n
am
= am − n
n
a
a
−n
1
a
= n ó  
a
b
−n
a ⋅b = n a ⋅ n b
a na
=
b nb
n
b
= 
a
n
a =
m n
m⋅n
a
Usar las leyes de los exponentes para simplificar la expresión:
(3a b c )
1)
(6 x y )(4 x y )
2)
4)
(x
8 x 3 y −5
5)
4 x −1 y 2
7)
(8 x
3
−3
4
5
y
y
3
)
2 −3
−3
)
 1 −5 2 
 x y 
2

3
2
(6 x )
(2 x )
4
2
 2x3   y 
  3 
3) 
 y  x 
6)
3 2
8)
2 3
(2 x
2
)(
)
1

y −5 6 x −3 y  x −1 y 3 
3

(3 y )(2 y )
(y )
2 2
3
9)
3
4 3
FACULTAD DE INGENIERIA Y CIENCIAS BASICAS
LOGICA Y PENSAMIENTO MATEMATICO – TALLER DE POTENCIACION Y RADICACION
DOCENTE: IDALY MONTOYA A.
(− 2 xy )
2 5
10)
 x7 
 3 
 8y 
 4a 2 b   5a 2 b 

13)  3 2  
4 
a
b
2
b



−2
11)
14)
 1 4 −3 
 xy 
3

(5x
2
)(
y −3 4x −5 y 4
)
12)
(3 y ) (4 y )
15)
(− 2 x
3 4
Simplifique la expresión y racionalice el denominador, cuando sea el caso:
2.1)
50
2.9)
3
320
2.2)
3
− 108
2.10)
2.3)
3
5
8
2.11)
3a 2 b 3
2.12)
9 x −4 y 6
3
2.4)
64
3
16 x 3 y 8 z 4
6a 5 b
8a 6 b −3
5
x7
2.13)
3
x7
2.14)
2.7)
x2 y
 − 8x 3  3
2.15)  − 6 
 y 
2.8)
x6
2.16)
2.5)
2.6)
3
16a 8 b −2
2
(25 z )
4
−3
2
4
2 −3
y −3
)
−2