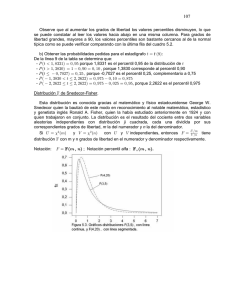
Estadística 21/22 Prácticas de estadística Para abrir los datos nos vamos a archivo abrir datos del programa statgraphics. a) Representa el gráfico de sectores y el diagrama de barras de las observaciones correspondiente a la variable Procedencia Para hacer esto le damos a describir, datos categóricos, tabulación, marcamos Procedencia en datos y marcamos las opciones que nos piden que son grafico de sectores y diagrama de barras. b) ¿Qué porcentaje de coches están fabricados en EEUU o Japón? Esto lo miramos en el diagrama de sectores. Vemos que en EEUU están fabricados el 16,77% y en Japón el 28,39% que suman un total de 45,16% c) Determina la media, la mediana, la desviación típica, los cuartiles y el recorrido intercuartílico de las observaciones de la variable «Consumo» Para hacer esto nos vamos a describir, datos numéricos, análisis de una variable. Me voy a resumen estadístico y le doy al botón derecho. Ahí tengo opciones de ventana en la que selecciono lo que me piden. Media: 8.7658, mediana: 8.2, la desviación típica: 2,45, la varianza 6.0348, recorrido intercuartílico: 3.5, cuartiles superior e inferior respectivamente:10.4 y 6.9. d) Haz un histograma de la variable «Consumo» que tenga 11 intervalos, siendo el límite inferior del primer intervalo 5 litros/100 km y el límite superior del último intervalo 16litros/100 km. Para esto nos tenemos que ir a graficar, gráficos explorativos, histograma, datos continuos. Cuando tengo el histograma le dos a opciones de ventana y le pongo el numero de clases que quiero y los dos limites que me dice el ejercicio. e) Para el histograma obtenido en el apartado anterior, ¿cuál es la marca de clase del intervalo donde se encuentra la media? Para saber cual es la marca de clase tenemos que sumar los limites superior e inferior del intervalo y dividirlo entre dos. En nuestro caso (5+16)/2=10.5 f) Representa el diagrama de caja-bigotes de «Consumo» e indica si hay observaciones anómalas. Para representar esto, al igual que antes me voy a describir, análisis de una variable para consumo y selecciono el diagrama de caja-bigotes. Vemos que SI hay una observación anómala. g) Determina el valor del percentil 10 y el percentil 90 de la variable «Consumo» Al igual que antes me voy a análisis de una variable, selecciono consumo y le pido los percentiles. El percentil 10 y el 90 son respectivamente 6.2 y 12.3. h) ¿Cuál es el mínimo valor de la variable «Consumo» del 20% de los coches que más consumo tienen? Aquí si nos fijamos en lo que nos pide tenemos que hacer el percentil 80 y ahí nos da el valor mínimo que consume el 20% de los coches que mas consumen que es 11.4. i) ¿Cuál es el máximo valor de la variable «Consumo» del 35% de los coches que menos consumen? Aquí hacemos el percentil 35. Nos da un valor de 7.3. j) ¿Qué porcentaje de coches tiene un consumo mayor o igual a 7 litros/100Km y menor que 12 litros/100km? 1 Estadística 21/22 k) Si se consideran las variables «Consumo» y «Potencia», ¿cuál de las dos variables presenta menor dispersión con respecto a su media? Gráfico de Dispersión 5 7 9 11 Consumo 13 Gráfico de Dispersión 15 17 50 70 90 110 Potencia 130 150 170 Nos hemos ido a comparación de datos, seleccionamos los dos y vemos que el que mayor coeficiente de variación tiene es el consumo. Es decir, el que presenta menor dispersión es la potencia. Resumen Estadístico Consumo 155 8,76581 6,03486 2,4566 28,0248% 5,2 15,7 10,5 3,74298 -0,880026 Recuento Promedio Varianza Desviación Estándar Coeficiente de Variación Mínimo Máximo Rango Sesgo Estandarizado Curtosis Estandarizada Potencia 155 88,1032 597,262 24,4389 27,739% 51,0 168,0 117,0 5,16351 1,81439 l) ¿Cuál es el valor de la covarianza entre las variables «Consumo» y «Potencia»? DUDA Tenemos que hacer un análisis multivariable para esto. Nos vamos a describir. Datos numéricos. Análisis multivariable. Y señalamos la covarianza. m) Determina la recta de regresión que nos permite pronosticar el consumo a partir de la potencia del motor. Calcula el error cuadrático medio. ¿Cuál es la predicción para una potencia de 160 CV? Tenemos que ir a relacionar, un factor, regresión simple, y marcamos la variable independiente Y que en este caso es la potencia con la variable dependiente X que es el consumo. La recta es: Potencia = 13,8465 + 8,47118*Consumo El error cuadrático medio es: R-cuadrada = 72,5087 porciento; R-cuadrado (ajustado para g.l.) = 72,329 porciento. OJO: ¿predicción para 160CV? n) A partir de la recta de regresión obtenida en el apartado anterior, por cada unidad de potencia que aumenta el motor ¿cuánto aumenta o disminuye el consumo? DUDA o) Respecto al modelo en su conjunto, teniendo en cuenta los resultados del contraste ADEVA a un nivel de significación del 5%, ¿podemos decir que el modelo es estadísticamente significativo? 2 Estadística 21/22 p) ¿Cuál es el modelo con mejor coeficiente de determinación, entre los que plantea Statgraphics, para estimar el consumo en función de la potencia del motor? Calcula el error cuadrático medio para este modelo y la predicción para una potencia de 160 CV. q) Determina el polinomio de regresión de grado 2 para estimar el consumo en función de la potencia del motor. Calcula el error cuadrático medio para este modelo y la predicción para una potencia de 160 CV. Este se hace con Relacionar, polinomio, seleccionamos quien es X y quien es Y y nos da el error. R-cuadrada = 72,7266 porciento DUDA ¿predicción? r) De los tres modelos ajustados en este problema (recta, modelo mejor en StatGraphics y polinomio), ¿cuál de ellos es mejor modelo para explicar la relación entre las variables «Consumo» y «Potencia»? 3