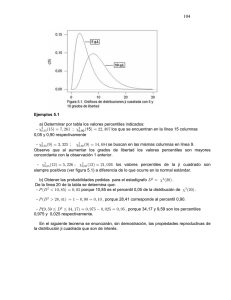
Observe que al aumentar los grados de libertad los valores

107
Observe que al aumentar los grados de libertad los valores percentiles disminuyen, lo que
se puede constatar al leer los valores hacia abajo en una misma columna. Para grados de
libertad grandes, mayores a 90, los valores percentiles son bastante cercanos al de la normal
típica como se puede verificar comparando con la última fila del cuadro 5.2.
b) Obtener las probabilidades pedidas para el estadígrafo > œ t Ð*Ñ:
De la línea 9 de la tabla se determina que:
- T Ð>  "ß )$$"Ñ œ !ß *& porque 1,8331 es el percentil 0,95 de la distribución de >
- T Ð>  "ß $)$!Ñ œ "  !ß *! œ !ß "! ß porque 1,3830 corresponde al percentil 0,90
- T (> Ÿ  !ß (!#(Ñ œ !ß #& ß porque -0,7027 es el percentil 0,25, complementario a 0,75
- T Ð  "ß $)$!  > Ÿ #ß #'##Ñ œ !ß *(&  !ß "! œ !ß )(&
- T Ð  #ß #'## Ÿ > Ÿ #ß #'##Ñ œ !ß *(&  !ß !#& œ !ß *&, porque 2,2622 es el percentil 0,975
Distribución … de Snedecor-Fisher.
Esta distribución es conocida gracias al matemático y físico estadounidense George W.
Snedecor quien la bautizó de este modo en reconocimiento al notable matemático, estadístico
y genetista inglés Ronald A. Fisher, quien la había estudiado anteriormente en 1924 y con
quien trabajaron en conjunto. La distribución es el resultado del cociente entre dos variables
aleatorias independientes con distribución ji cuadrada, cada una dividida por sus
correspondientes grados de libertad, m la del numerador y n la del denominador.
Y Î7
Si Y œ ;# Ð7Ñ
y Z œ ;# Ð8Ñ
con Y y Z independientes, entonces J œ Z Î8 tiene
distribución … con m y n grados de libertad en el numerador y denominador respectivamente.
Notación:
J œ …Ð7 ß 8Ñ ; Notación percentil alfa : …! Ð7 ß 8Ñ.